Форма поверхности жидкости вблизи стенок сосуда
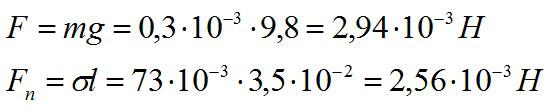
Авторы: А. М. Емельяненко, Н. В. Чураев
КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ, совокупность явлений, обусловленных поверхностным натяжением на границе раздела несмешивающихся сред (в системах жидкость – жидкость, жидкость – газ или пар) при наличии искривления поверхности. Частный случай поверхностных явлений.
Рис. 1.
При отсутствии силы тяжести жидкость ограниченной массы под воздействием поверхностного натяжения стремится занять объём с миним. поверхностью, т. е. принимает форму шара. В условиях действия силы тяжести не слишком вязкая жидкость достаточной массы принимает форму сосуда, в который налита, и её свободная поверхность при относительно большой площади (вдали от стенок сосуда) становится плоской, т. к. роль поверхностного натяжения менее существенна, чем силы тяжести. При взаимодействии с поверхностью др. жидкости или твёрдого тела (напр., со стенками сосуда) поверхность рассматриваемой жидкости искривляется в зависимости от наличия или отсутствия смачивания. Если имеет место смачивание, т. е. молекулы жидкости 1 (рис. 1) сильнее взаимодействуют с молекулами поверхности 3, чем с молекулами др. жидкости (или газа) 2, то под воздействием разности сил межмолекулярного взаимодействия жидкость 1 поднимается по стенке сосуда – участок жидкости, примыкающий к стенке, искривляется. Давление, вызываемое подъёмом жидкости, уравновешивается капиллярным давлением $Delta p$ – разностью давлений над и под искривлённой поверхностью раздела. Величина капиллярного давления зависит от среднего радиуса $r$ кривизны поверхности и определяется формулой Лапласа: $Delta p=2 sigma/r$, где $sigma$ – поверхностное натяжение. Если граница раздела фаз плоская ($r= infty$), то в условиях механич. равновесия системы давления с обеих сторон границы раздела равны и $Delta p=0$. В случае вогнутой поверхности жидкости ($r lt 0$) давление в жидкости ниже, чем давление в граничащей с ней фазе и $Delta p lt 0$; для выпуклой поверхности ($r>0$) $Delta p>0$.
Если стенки сосуда приблизить друг к другу, зоны искривления поверхности жидкости образуют мениск – полностью искривлённую поверхность. Образовавшаяся система называется капилляром; в нём в условиях смачивания давление под мениском понижено и жидкость в капилляре поднимается (над уровнем свободной поверхности жидкости в сосуде); вес столба жидкости высотой $h$ уравновешивает капиллярное давление $Delta p$. Несмачивающая жидкость в капилляре образует выпуклый мениск, давление над которым выше, и жидкость в нём опускается ниже уровня свободной поверхности вне капилляра. Высота поднятия (опускания) жидкости в капилляре относительно свободной поверхности (где $r= infty$ и $Delta p=0$) определяется соотношением: $h=2 sigma cos theta/ Delta rho gr$, где $theta$ – краевой угол (угол между касательной к поверхности мениска и стенкой капилляра), $Delta rho$ – разность плотностей жидкости 1 в капилляре и внешней среды 2, $g$ – ускорение свободного падения.
Искривление поверхности влияет на условия равновесия между жидкостью и её насыщенным паром: согласно Кельвина уравнению, давление паров над каплей жидкости повышается с уменьшением её радиуса, что объясняет, напр., рост больших капель в облаках за счёт малых.
Рис. 2.
К характерным К. я. относятся капиллярное впитывание, появление и распространение капиллярных волн, капиллярное передвижение жидкости, капиллярная конденсация, процессы испарения и растворения при наличии искривлённой поверхности. Капиллярное впитывание характеризуется скоростью, зависящей от капиллярного давления и вязкости жидкости. Оно играет существенную роль в водоснабжении растений, движении воды в почвах и др. процессах, связанных с движением жидкостей в пористых средах. Капиллярная пропитка – один из распространённых процессов химич. технологии. В системах с непараллельными стенками (или капиллярах конич. сечения) кривизна менисков зависит от расположения в них граничных поверхностей жидкости, и капля смачивающей жидкости в них начинает двигаться к мениску с меньшим радиусом (рис. 2), т. е. в ту сторону, где давление ниже. Причиной капиллярного передвижения жидкости может служить и разница сил поверхностного натяжения в менисках, напр. при существовании градиента темп-ры или при адсорбции поверхностно-активных веществ, снижающих поверхностное натяжение.
Капиллярной конденсацией называют процесс конденсации пара в капиллярах и микротрещинах пористых тел, а также в промежутках между сближенными твёрдыми частицами или телами. Необходимое условие капиллярной конденсации – наличие смачивания поверхности тел (частиц) конденсирующейся жидкостью. Процессу капиллярной конденсации предшествует адсорбция молекул пара поверхностью тел и образование менисков жидкости. В условиях смачивания форма менисков вогнутая и давление $p$ насыщенного пара над ними ниже, чем давление насыщенного пара $p_0$ при тех же условиях над плоской поверхностью. Т. е. капиллярная конденсация происходит при более низких, чем $p_0$, давлениях.
Искривление поверхности жидкости может существенно влиять на процессы испарения, кипения, растворения, зародышеобразования при конденсации пара и кристаллизации. Так, свойства систем, содержащих большое количество капель или пузырьков газа (эмульсий, аэрозолей, пен), и их формирование во многом определяются К. я. Они лежат также в основе мн. технологич. процессов: флотации, спекания порошков, вытеснения нефти из пластов водными растворами поверхностно-активных веществ, адсорбционного разделения и очистки газовых и жидких смесей и т. п.
Впервые К. я. были исследованы Леонардо да Винчи. Систематич. наблюдения и описания К. я. в тонких трубках и между плоскими, близко расположенными стеклянными пластинами провёл в 1709 Ф. Хоксби, демонстратор Лондонского королевского об-ва. Основы теории К. я. заложены в трудах Т. Юнга, П. Лапласа, а их термодинамич. рассмотрение осуществил Дж. Гиббс (1876).
Источник
Силы, возникающие на кривой поверхности жидкости.
Молекула находится в равновесии, если эта сила направлена перпендикулярно к поверхности жидкости.
Рис.20.4
При смачивании сила направлена в сторону стенки.
Если жидкость не смачивает стенку, то сила направлена в сторону жидкости.
Искривление поверхности жидкости (например, вблизи стенки сосуда) приводит к появлению сил, действующих на жидкость под этой поверхностью и к повышению давления внутри жидкости.
Рассмотрим сферическую каплю жидкости с радиусом сферы r (рис. 20.5). при уменьшении радиуса капли свободная энергия уменьшается и жидкость под сферической поверхностью всегда испытывает дополнительное давление, направленное внутрь.
Пусть под действием этого давления капля уменьшит свой объем на dV, (рис.). Работа сжатия жидкости произведена, очевидно, за счет уменьшения свободной энергии.
Рис.20.5
Работа сжатия dA равна
dA = pdV. (20.14)
где р – давление. Уменьшение свободной энергии
dF =σdS, (20.15)
где dS – уменьшение поверхности шара, соответствующее уменьшению радиуса на dr. Из известных формул для поверхности и объема шара
получим выражения:
.
Подставляя эти значения для dS и dV в уравнения (20.14) и (20.15) и принимая во внимание, что модули dA и dF равны, получим:
.
Отсюда следует выражение для давления, оказываемого на жидкость искривленной сферической поверхностью:
. (20.16)
Аналогично можно получить выражение для цилиндрической поверхности жидкости:
.
Для поверхности любой формы давление, обусловленное кривизной поверхности, выражается уравнением Лапласа:
,
где r1 и r2 – радиусы кривизны любых взаимно перпендикулярных сечений в данной точке поверхности/
Если жидкость находится в узком сосуде, влияние стенок простирается на всю поверхность жидкости. Если размеры сосуда, в котором находится жидкость, или, если расстояние между поверхностями, ограничивающими жидкость, сравнимы с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярными.Явления, происходящие в узких сосудах, называются капиллярными явлениями.
Дополнительное давление Лапласа вызываеткапиллярный подъем.
Рис.20.5
Случай смачивания
Вследствие давления, вызванного кривизной поверхности, жидкость, заполняющая трубку, испытывает давление р, направленное к центру кривизны мениска, т. е. вверх, и равное 2σ/r0. Под действием этого давления жидкость поднимается по трубке до уровня h, при котором гидростатическое давление ρgh столба жидкости высотой h уравновешивает давление р.
Условие равновесия:
. (20.17)
где ρ – плотность жидкости, а g – ускорение силы тяжести. Это равенство определяет высоту подъема жидкости в капилляре.
Найдем связь между высотой подъема h и радиусом трубки r. Центр сферы, частью которой является мениск, находится в точке О. Из чертежа следует
.
Поэтому (20.17) перепишется в виде
.
Отсюда
. (20.18)
Из (20.18) следует, что, высота подъема жидкости в капилляре растет с уменьшением радиуса. капилляра и с увеличением коэффициента поверхностного натяжения жидкости.
Капиллярным подъемом объясняются такие известные явления как впитывание жидкости фильтровальной бумагой, перенос керосина вдоль фитиля, волокна которого также являются тонкими капиллярами, перенос жидкости в пористых телах. Капиллярные силы обеспечивают подъем воды из почвы по стволам деревьев, где волокна древесины играют роль тонких капилляров.
Источник
Капилля́рные явления – изменение уровня жидкости в очень тонких трубках – капиллярах. Если диаметр капилляра мал, то мениски, образующиеся у его стен, сливаются друг с другом, образуя поверхность, близкую к сферической. Силы поверхностного натяжения действуют по касательной к поверхности жидкости вдоль всей границы ее поверхности. В данном случае граница – это окружность, диаметр которой равен диаметру капилляра. К капиллярным относят явления в жидких средах, вызванные искривлением их поверхности, граничащей с другой жидкостью, газом или собственным паром.
Капиллярные явления охватывают различные случаи равновесия и движения поверхности жидкости под действием сил межмолекулярного взаимодействия и внешних сил, в первую очередь, силы тяжести. Когда внешние силы отсутствуют или скомпенсированы, поверхность жидкости всегда искривлена. Так, в условиях невесомости ограниченный объем жидкости, не соприкасающийся с другими телами, принимает под действием поверхностного натяжения форму шара. Эта форма отвечает устойчивому равновесию жидкости, поскольку шар обладает минимальной поверхностью при данном объеме и, следовательно, поверхностная энергия жидкости в этом случае минимальна. Форму шара жидкость принимает и в этом случае, если она находится в другой, равной по плотности жидкости (действие силы тяжести компенсируется архимедовой выталкивающей силой).
Сферическая форма капли жидкости при соприкосновении с поверхностью твердого тела не сохраняется. Изменение формы капли зависит от материала, из которого сделано твердое тело. На стекле капля растекается, а на поверхности парафина приобретает форму сплюснутого шара.
Зависимость формы капли от материала подложки объясняется различием сил взаимодействия между молекулами жидкости и сил взаимодействия молекул жидкости с молекулами твердого тела на границе раздела двух сред.
Смачивающей называют жидкость, которая растекается тонкой пленкой по твердому телу. Несмачивающей называют жидкость, которая не растекается по твердому телу, а стягивается в каплю.
Мера смачиваемости – это угол (theta)между смачиваемой поверхностью и касательной к поверхности жидкости. Его называют углом смачивания, или краевым углом. Для смачивающей жидкости угол смачивания острый, для несмачивающей жидкости угол смачивания тупой.
При контакте твердых, жидких или газообразных тел на их границе устанавливается равновестие. При этом на каждый элемент границы будет действовать три силы:
(vec{F_{жг}})- сила между жидкостью и газом,
(vec{F_{тж}})- сила между твердым телом и жидкостью,
(vec{F_{тг}})- сила между твердым телом и газом.
Растекание жидкости просходит, если: (vec{F_{тг}} geq vec{F_{тж}} + vec{F_{жг}}costheta )
Из условия равновесия следует: (vec{F_{тг}} = vec{F_{тж}} + vec{F_{жг}}costheta ).
Отсюда (costheta = {vec{F_{тг}} – vec{F_{тж}} over vec{F_{жг}}})
Если (vec{F_{тж}})< (vec{F_{тг}}), то (costheta > 0), жидкость смачивающая.
Если (vec{F_{тж}})> (vec{F_{тг}}), то (costheta < 0), жидкость несмачивающая.
Если (vec{F_{тг}}) -(vec{F_{тж}} )> (vec{F_{тж}} ), то равновесие не соблюдается. Значит, жидкость полностью смачивает твердое тело, отделяя его от газа.
Хорошее смачивание необходимо при нанесении красочных покрытий, обработке фотоматериалов, пайке, стирке. Использование веществ с минимальной смачиваемостью требуется для гидроизоляции, например, при изготовлении материала для плащей, курток, зонтов.
Смачивание твердых поверхностей жидкостью характеризуется мениском и углом смачивания. Мениском называют форму поверхности жидкости вблизи стенки сосуда. Мениск зависит от того, смачивает или не смачивает жидкость стенки сосуда.
Действием поверхностного натяжения вызывается избыточное давление под искривленной поверхностью:
(p = {F over s} = {sigma2pi Rover pi R^2} = {2sigma over R})
где(sigma)- поверхностное натяжение.
Если поверхность выпуклая – давление увеличивается, если вогнутая – уменьшается.
Капиллярность – это явление подъема или опускания жидкости в капиллярах. В достаточно широких сосудах короткоживущие силы притяжения между молекулами твердого тела и жидкости удерживают в виде мениска лишь незначительную часть жидкости в сосуде. основная поверхность – горизонтальная. В узких сосудах (капиллярах) масса жидкости невелика, поэтому различие между силой притяжения между молекулами жидкости и твердого тела и силой притяжения между молекулами жидкости приводит к капиллярности.
Когда капилляр опущен в жидкость, то в случае смачивающей жидкости силы притяжения между молекулами жидкости и твердого тела Fж-т, то есть стенками капилляра, превосходят силы взаимодействия между молекулами жидкости Fж.
Жидкость втягивается внутрь капилляра. Подъем жидкости в капилляре происходит до тех пор, пока результирующая сила Fв действующая на жидкость вверх, не уравновесится силой тяжести mg столба жидкости высотой h:
Fв = mg.
Жидкость, не смачивающая стенки капилляра, опускается в нем на расстояние h.
Высота столба смачивающей жидкости в капилляре:
(h = {2sigma over rho gR})
(rho)- плотность жидкости.
Чем меньше радиус капилляра, тем больше высота подъема жидкости в капилляре. Так, лежащий на мокрой губке сухой кусок мела быстро намокает, в то время как сухая губка, лежащая на мокром куске мела, остается сухой. Этот оффект объясняется тем, что капилляры у мела тоньше, чем у губки.
Многочисленные капиляры, пронизывающие растительные и животные ткани, почву, играют важную роль в водоснабжении и обмене веществ растений и животных.
- Справочник школьника. Ваш домашний репетитор по программе 5-11 класса. Том 2. СПб: ИГ Весь, 2006.
- В.А. Касьянов Физика. 10 класс. М: Дрофа, 2002
- Физический энциклопедический словарь. БСЭ, 1995.
Источник
Сегодня поверхностно рассматриваем тему поверхностного натяжения и решаем соответствующие задачи по физике.
Даже если вы не большой любитель жидкости, подписывайтесь на наш телеграм-канал, это интересно и полезно для всех.
Поверхностное натяжение, задачи
Задача №1. Поверхностное натяжение
Условие
Для определения коэффициента поверхностного натяжения воды была использована пипетка с диаметром выходного отверстия d=2 мм. Оказалось, что n=40 капель имеют массу m=1,9 г. Каким по этим данным получится коэффициент поверхностного натяжения «сигма»?
Решение
На каплю действует сила тяжести и сила поверхностного натяжения. Эти силы уравновешивают друг друга. Из условия задачи можно найти массу одной капли m0 и длину ее окружности l:
Далее запишем условие равновесия капли:
Отсюда находим коэффициент поверхностного натяжения:
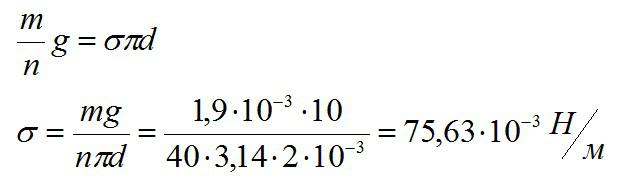
Ответ: 75,63*10^-3 Н/м.
Задача №2. Капиллярные явления
Условие
В капиллярной трубке радиусом 0,5 мм жидкость поднялась на высоту 11 мм. Оценить плотность данной жидкости, если ее коэффициент поверхностного натяжения равен 22 мН/м.
Решение
Для капилляра существует формула:
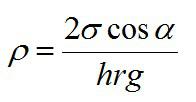
Альфа в этой формуле – угол смачивания стенки капилляра жидкостью. Пример его равным 90 градусов.
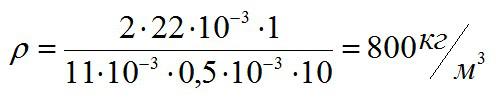
Ответ: 800 килограмм на кубический метр.
Задача №3. Поверхностное натяжение
Условие
В дне сосуда со ртутью имеется круглое отверстие диаметром 70 мкм. При какой максимальной высоте слоя ртути H она не будет вытекать через отверстие?
Решение
Ртуть не будет вытекать до тех пор, пока сила ее давления не превысит силу поверхностного натяжения:
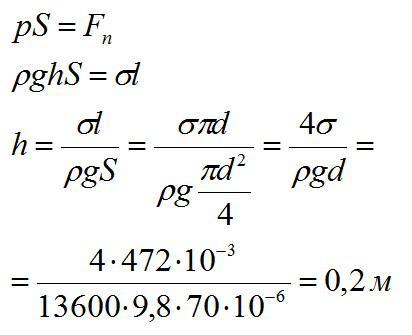
Значения коэффициента поверхностного натяжения разных жидкостей берутся в справочнике.
Ответ: 0,2 м.
Задача №4. Поверхностное натяжение
Условие
Швейная игла имеет длину 3,5 см и массу 0,3 г. Будет ли игла лежать на поверхности воды, если ее положить аккуратно?
Решение
Найдем силу тяжести, которая действует на иглу и сравним ее с силой поверхностного натяжения.
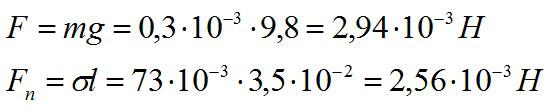
Ответ: Так как сила тяжести больше, игла утонет.
Задача №5. Поверхностное натяжение
Условие
Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г.
Решение
На кольцо действуют силы поверхностного натяжения, сила тяжести и внешняя сила, стремящаяся оторвать кольцо от поверхности. Найдем силу поверхностного натяжения:
Множитель «2» используется в формуле, так как кольцо взаимодействует с жидкостью двумя своими сторонами.
Теперь запишем условие отрыва кольца:
Значение поверхностного натяжения мыльного раствора при комнатной температуре возьмем из таблицы, подставим числа, и получим:
Ответ: 0,11 Н.
Вопросы на тему «Поверхностное натяжение и свойства жидкостей»
Вопрос 1. Что такое жидкость?
Ответ. Жидкость – физическое тело, которое не может самостоятельно сохранять свою форму. Агрегатное состояние вещества между твердым телом и газом.
Вопрос 2. Какие свойства жидкости вы знаете?
Ответ. Среди основных свойств жидкости можно выделить:
- текучесть;
- вязкость;
- сохранение объема;
- поверхностное натяжение.
Вопрос 3. Что такое поверхностное натяжение?
Ответ. Поверхностное натяжение – это явление, при котором жидкость стремиться приобрести форму с наименьшей возможной площадью поверхности.
Примеры поверхностного натяжения в природе:
- Именно благодаря поверхностному натяжению в поле силы тяжести Земли жидкость приобретает форму капли.
- В отсутствие силы тяжести жидкости капля примет шарообразную форму.
- Водомерка удерживается на поверхности воды благодаря силе поверхностного натяжения.
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью S при постоянной температуре.
Вопрос 4. Что такое капиллярные явления?
Ответ. Капиллярные явления – подъем или опускание жидкости в капиллярах (трубках малого диаметра).
Вопрос 5. Что называется смачиванием?
Ответ. Смачивание – это искривление поверхности жидкости вблизи твердого тела. Возникает из-за взаимодействия молекул жидкости с молекулами твердого тела.
Количественная характеристика этого явления – угол смачивания.
Нужна помощь в решении заданий по учебе? Профессиональный студенческий сервис всегда готов ее оказать! Оформляйте заявку в любое время суток и забудьте о наболевших вопросах.
Источник
