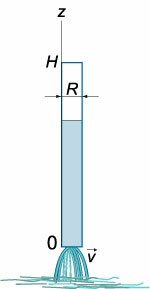
Форма сосуда для постоянной скорости
Сегодня я заварил себе чай и задумался
Сегодня утром я задумался, пока размешивал два кубика сахара в чашке с только что заваренным чаем. Задумался о форме жидкости, которую она принимает при вращении. Безусловно, все представляют себе что будет, если очень быстро начать размешивать сахар в чашке с чаем. Мне захотелось рассмотреть этот банальный и привычный процесс подробнее и попытаться рассказать Вам немного интересного из физики окружающих нас в быту явлений.
Идея эксперимента
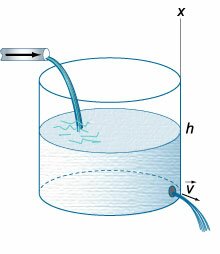
Давайте представим, что мы имеем некоторую цилиндрическую тару, в которой находится некоторая жидкость. Вращаться жидкость можно заставить, как минимум, двумя очевидными способами: размешать её каким-нибудь предметом или начать вращать цилиндрическую тару, что, благодаря силам трения между жидкостью и поверхностью сосуда, приведет к вращению жидкости, увлекаемой содержащим её вращающимся сосудам.
Физическая модель
Остановимся на втором варианте. Итак, у нас есть вращающийся с постоянной циклической частотой сосуд, в котором при динамическом равновесии с постоянной циклической частотой вращается жидкость в том же направлении.
Вырежем из всей жидкости элементарный бесконечно малый объем около поверхности и рассмотрим какие силы на него действуют. В силу симметрии задачи, будем ориентироваться на цилиндрические координаты, что заметно упростит расчеты.
Качественный расчет формы поверхности
Запишем второй закон Ньютона для элементарного кусочка объема жидкости:
К примеру, после размешивания ложкой сахара в чашке только что заваренного чая, жидкость вращается вокруг оси симметрии, отсюда наш элементарный кусочек объема имеет центростремительное ускорение. Поэтому спроецируем наш закон Ньютона на ось, совпадающую с радиусом-вектором от элементарного объема до оси симметрии. Не будем учитывать вязкость и поверхностное натяжение. Сила, сообщающая центростремительное ускорение (в правой части нашего закона движения) возникнет из-за разности давлений столбов жидкости, что можно увидеть на увеличенной части первого рисунка.
Таким образом, у нас получится следующее выражение:
, где , а та самая сила определится как , где площадью эффективного сечения обозначена та площадь нашего элементарного объема, на которую действует разница давлений столбов жидкости .
Получаем силу
Масса нашего элемента объема определяется по знакомой всем формуле , а сам объем будет равен (элементарный объем в цилиндрических координатах).
В итоге, 2 закон Ньютона для нашей маленькой задачки расписывается в следующее выражение:
После небольших сокращений и преобразований получаем:
Теперь проинтегрируем обе части выражения, используя неопределенные интегралы:
Детальный расчет формы поверхности
Теперь мы получили вполне ясную зависимость для формы поверхности и с уверенностью можем сказать, что это параболоид. Но нам неизвестна постоянная величина . Давайте её определим для полного понимания физики процесса.
Так как объем жидкости не меняется (мы считаем, что не пролили ни капли, пока размешивали наш чай ツ), то запишем объемы до вращения и во время вращения с постоянной циклической частотой.
До вращения:
, где — это высота жидкости в цилиндрической поверхности в спокойном состоянии (вращения нет).
Во время вращения:
Данные объемы равны, поэтому:
Отсюда выражается ранее неизвестная постоянная:
И окончательное уравнение формы поверхности вращающейся жидкости имеет вид:
или преобразовав
Некоторые заметки
Хотелось бы обратить внимание на то, что форма поверхности зависит от частоты вращения, ускорения свободного падения, геометрических параметров сосуда, первоначального объема жидкости, но не зависит от плотности жидкости. Это выражение мне показалось довольно интересным, так как с его помощью можно легко смоделировать примерное расположение жидкости внутри вращающегося вокруг своей оси симметрии цилиндрического сосуда. Для этого можно воспользоваться MathCAD’ом и построить несколько графиков.
Графическое представление результатов расчета
Возьмем вполне реальные параметры системы, соизмеримые с размерами чашки или стакана.
Радиус цилиндрической поверхности:
Высота жидкости в цилиндрической поверхности без вращения:
Ускорение свободного падения:
Циклическая частота вращения цилиндрической поверхности:
(Все значения этих величин заданы в системе Си)
Далее перепишем нашу функцию для её отображения в MathCAD.
Для 2D отображения сечения:
Для 3D отображения поверхности:
В качестве изменяющегося параметра будем менять циклическую частоту вращения . Результаты можно наблюдать на рисунках ниже:
При циклической частоте
При циклической частоте
При циклической частоте
При циклической частоте
При циклической частоте
При циклической частоте
Выводы
Видно, что если циклическая частота превысит значение , то мы увидим дно вращающегося цилиндрического сосуда, и, начиная с этой частоты, жидкость будет плавно «переходить» на стенки сосуда, всё сильнее оголяя дно. Очевидно, что при очень больших частотах вся жидкость растечется по стенкам сосуда. Теперь мы знаем все параметры такой жидкости. Зная её уравнение, не составит большого труда рассчитать толщину слоя жидкости на стенке сосуда на определенной высоте при определенной частоте.
upd. Отдельно хотелось бы подчеркнуть те противоречащие друг другу допущения, которые были приняты при рассмотрении задачи:
1. Считалось что, жидкость вращается благодаря вращению сосуда, который её содержит. Это может быть только при учете внутреннего трения, вязкости и поверхностного натяжения.
2. Но при выводе формы поверхности эти явления не учитываются для того, чтобы упростить решение и показать только качественный результаты моделирования. Т.е. решение немного противоречит описываемой изначально модели. Учет всех явлений, включая нелинейность процесса при высоких частотах, настолько бы усложнил задачу, что её вряд ли можно было бы решить аналитически и показать примерную и понятную модель для человека, который не связан с математикой/физикой.
3. Цель состоялась в том, чтобы показать лишь очень приближенное и самое простое решение, включающее в себя ряд допущений.
Источник
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
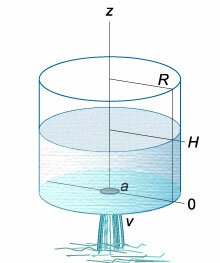
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
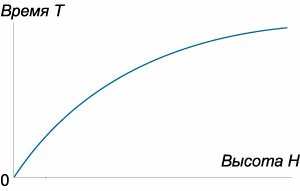
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
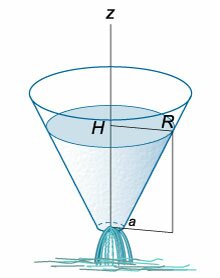
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
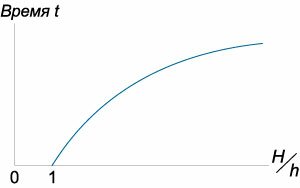
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
2 Редакция
Объект в движении меняет волны частоту. Когда кровяное тельце стремится К излучателю — отраженная частота выше, ОТ излучателя — отраженная частота ниже.
Источник и приемник УЗ-волны находятся в датчике. Прибор замеряет допплеровский сдвиг частоты: ΔF=(Fд-Fо), где Fд — частота датчик, Fо — отраженная частота.
Нажимайте на картинки, чтобы увеличить.
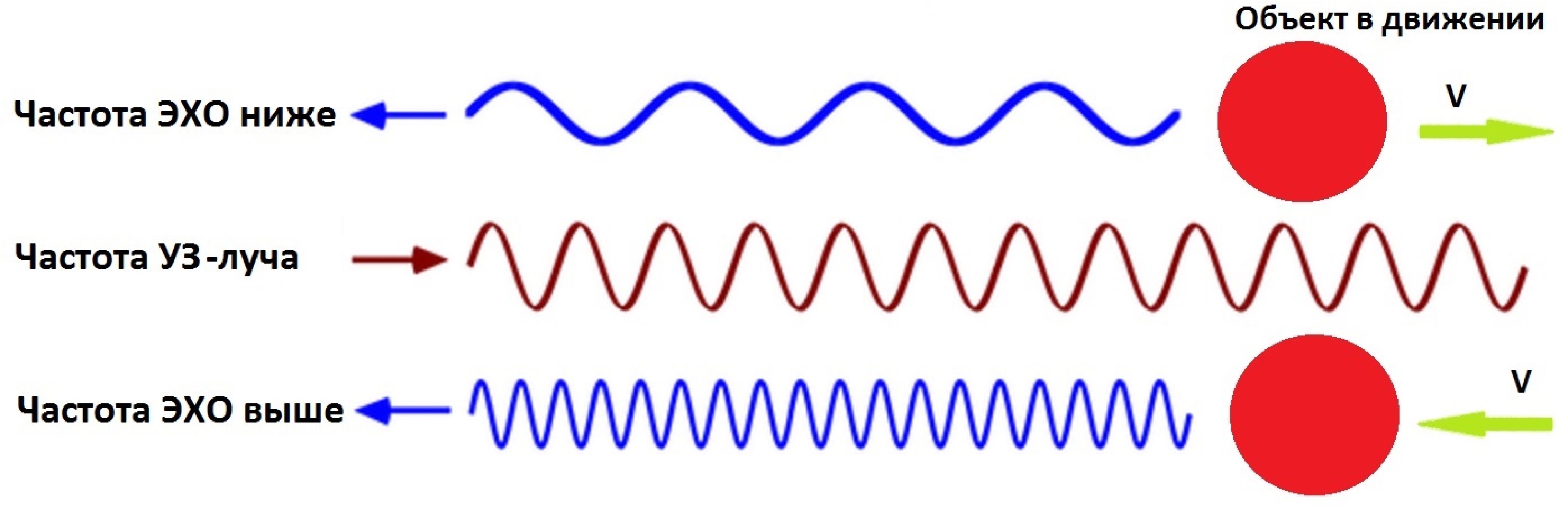
УЗ-волна ложится на вектор скорости под ∠α. ΔF определяет проекция вектора скорости на УЗ-луч (V·cosα): ΔF=2Fд·V·cosα/C, С — скорость звука в мягких тканях 1540 м/с.
Для оценки скорости кровотока используют уравнение Доплера: V=ΔF·C/2Fд·cosα. Когда УЗ-луч проникает в сосуд под ∠90° ⇒ cosα=0, невозможно оценить скорость кровотока.
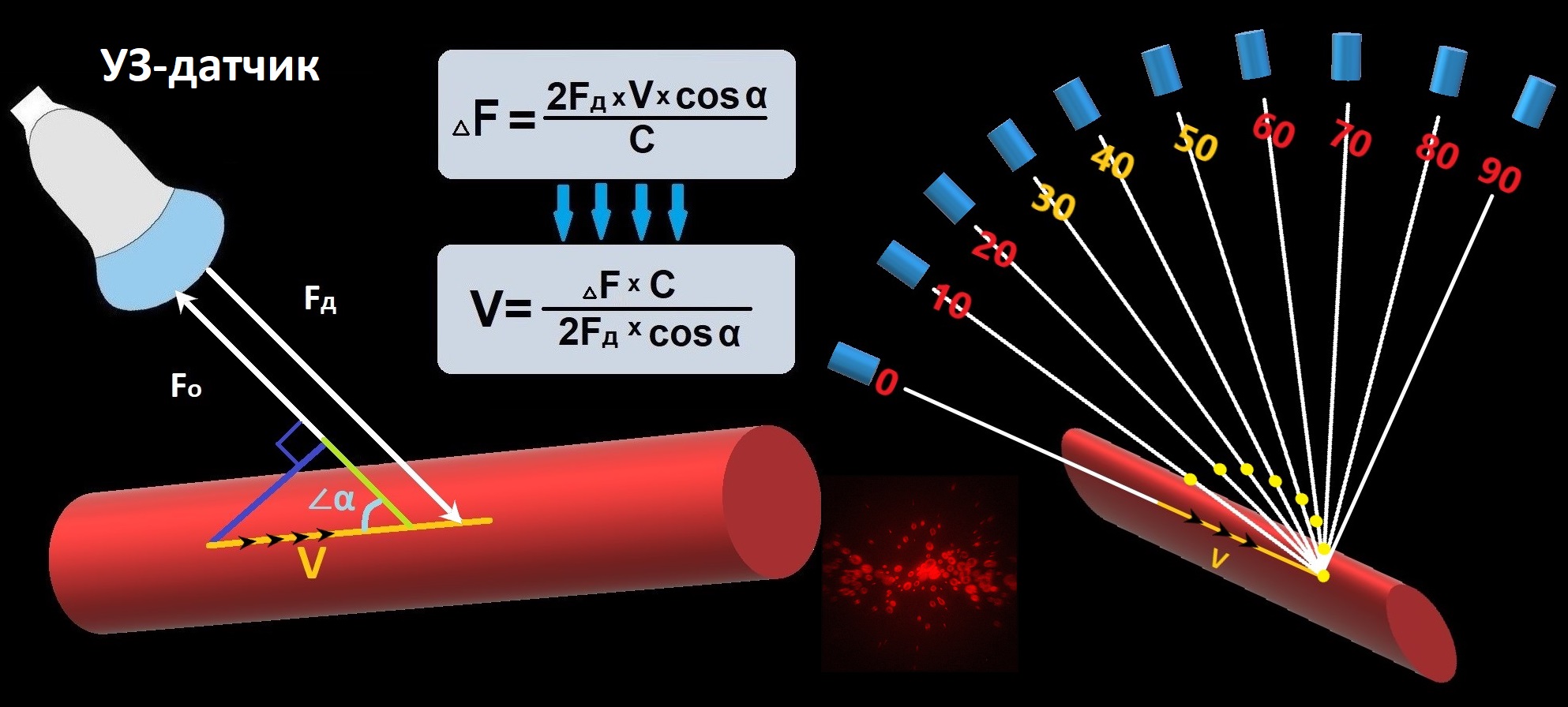
Для ∠0-60° величина cosα от 1 до 0,5; для ∠60-90° величина cosα от 0,5 до 0. Коротко от 90° величина Vcosα мала ⇒ ΔF небольшой ⇒ скорость неточная.
Когда ∠α ниже 25°, УЗ-луч почти полностью отражается от стенки сосуда. Чтобы определить скорость потока, направляете УЗ-луч под углом 25-60°.
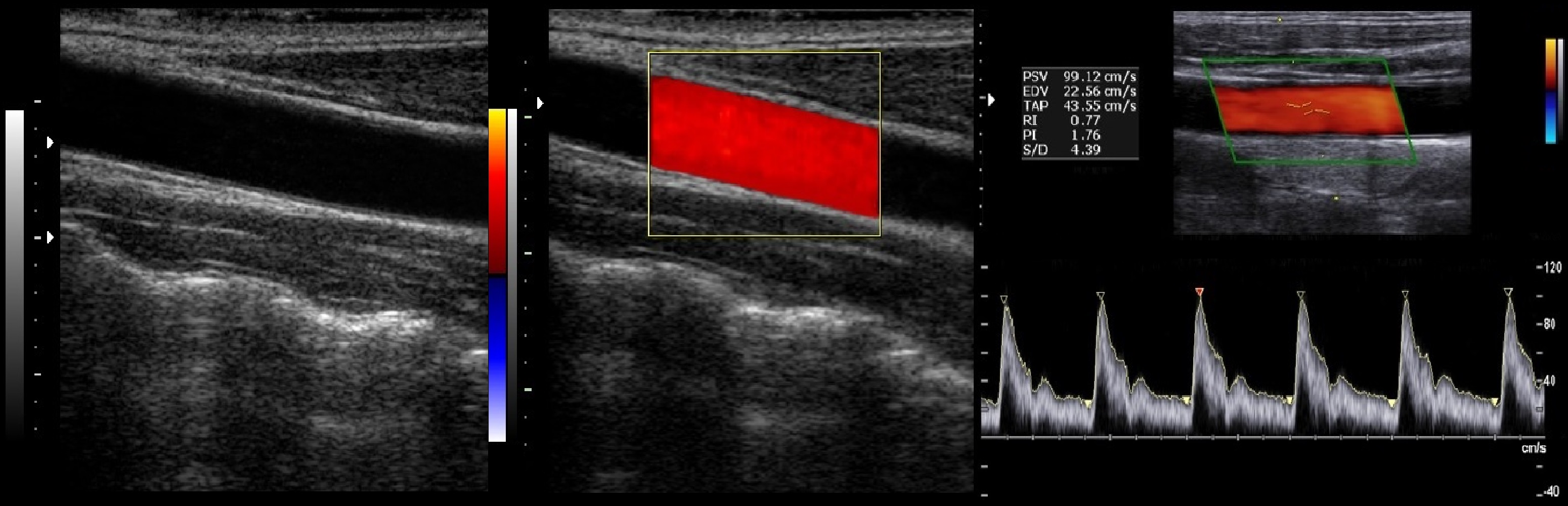
Дуплексное и триплексное сканирование сосудов
Три уровня УЗИ сосудов: серая шкала (В-режим), цветное доплеровское картирование (ЦДК) и спектральная доплерография (D-режим).
Дуплексное сканирование сосудов — В-режим и ЦДК, B-режим и D-режим; триплексное сканирование сосудов — В-режим, ЦДК и D-режим.
ЦДК кодирует скорость и направление в оттенки красного и синего: темные и светлые тона — низкие и высокие скорости. Когда зашкаливает cкорость, пропадает цвета чистота.
Радужные переливы (элайзинг) указывают высокоскоростной поток в месте стеноза. Настройте шкалу скорости: 4 см/с — низкая, 115 см/с — высокая, 39 см/с — правильная.
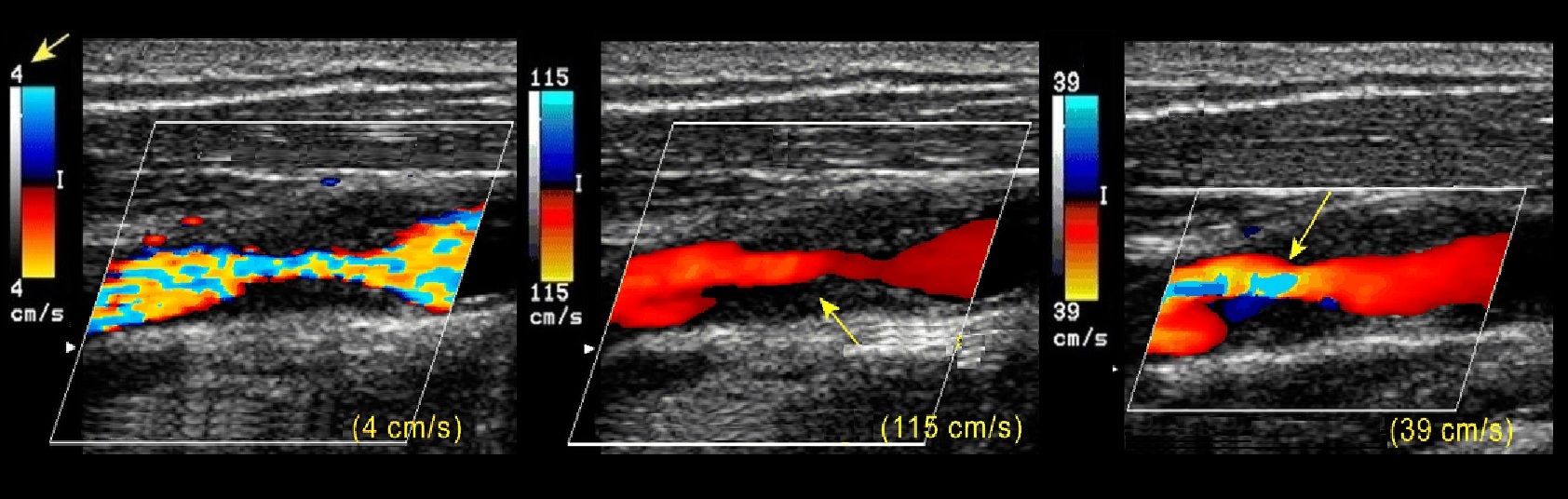
Энергетический доплер кодирует скорость, но не направление, в оттенки одного цвета; полезный в извитых сосудах и на маленьких скоростях.
Задача.
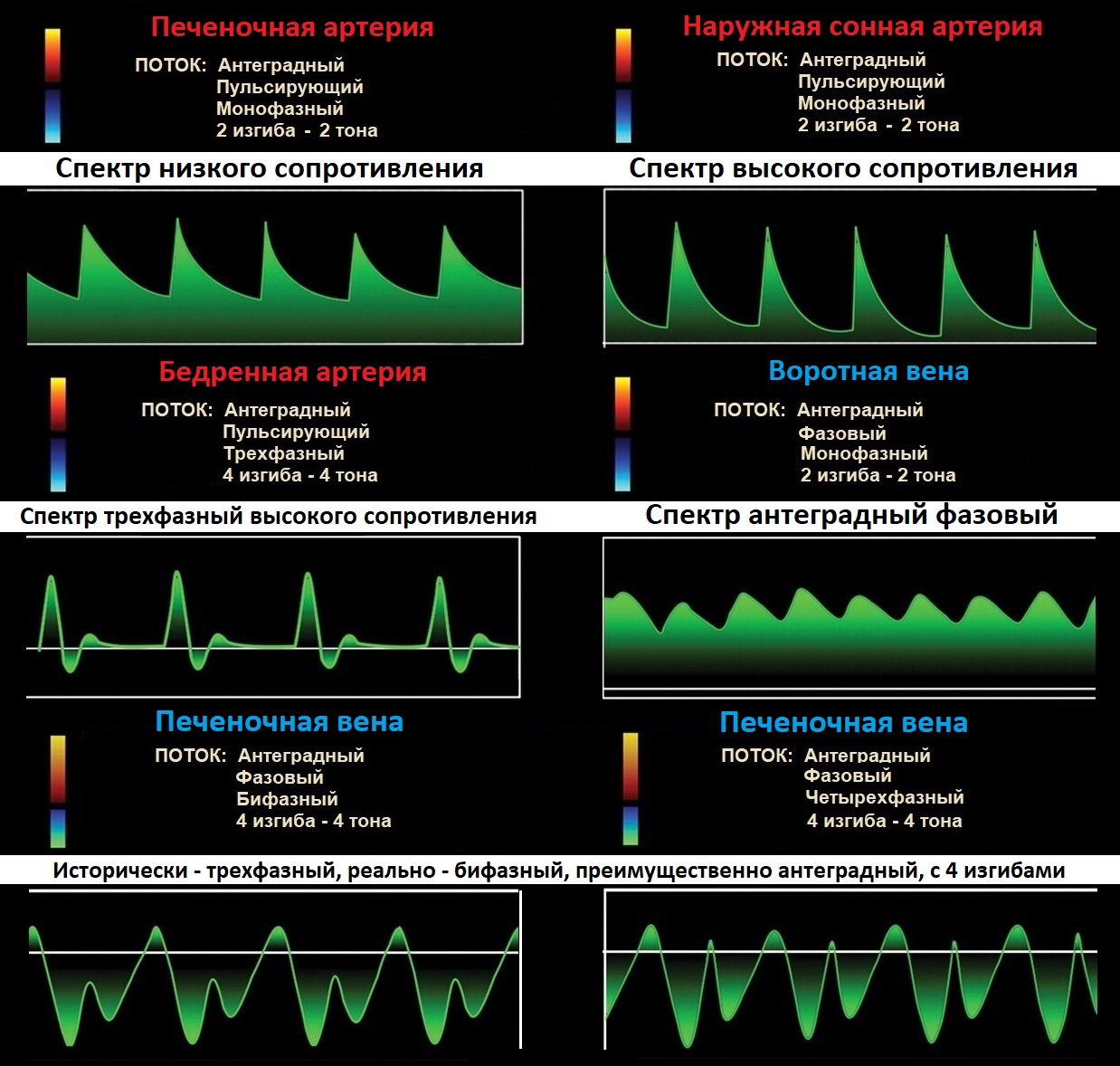
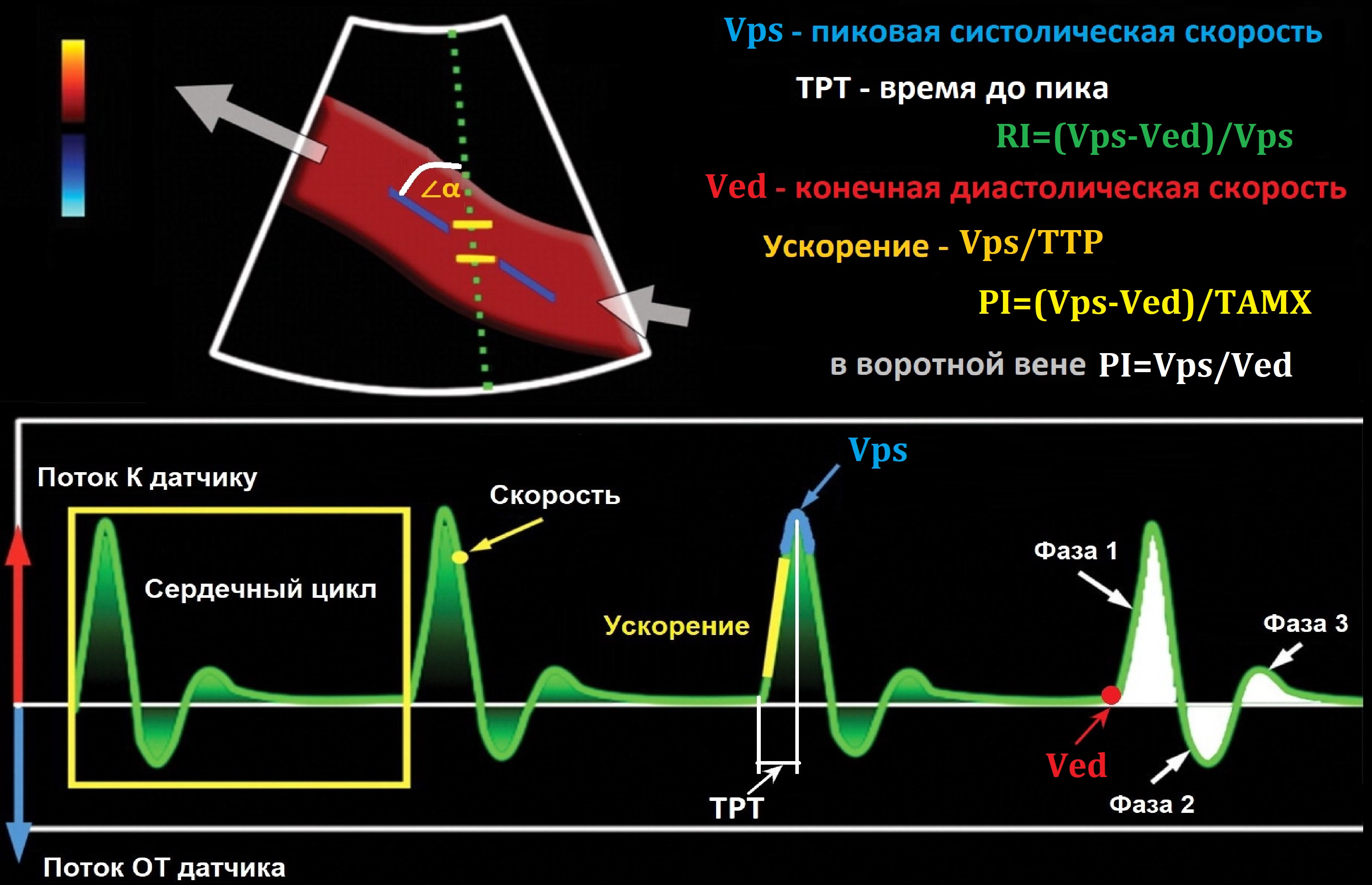
Спектр получают из ворот в центре сосуда. Вертикальная ось — шкала скорости; горизонтальная — время; базовая линия обрезает поток К и ОТ датчика.
Спектр может пересекать базовую линию; составляющие по разные стороны называют фазами. Спектр может быть моно-, би-, трех- и четырехфазный.
Как измерить скорость кровотока
1. Ворота поместите в центр сосуда (трэкбол), длину установите на 2/3-4/5 просвета (SVlength);
2. Угол между УЗ-лучом и осью сосуда 25-60°, курсор вдоль потока;
3. Спектр занимает 2/3-4/5 шкалы скорости (PRF), временная развертка на 2-3 цикла;
4. Для артерий спектр располагают выше базовой линии, для вен — ниже (Invert).
5. Отрегулируйте усиление (GAIN), чтобы контур спектра был четкий.
6. Обведите спектр и получите отчет — Vps, Ved, RI, PI и др.
Задача. УЗ-луч и сосуд под ∠90° (1) — спектр неясный; исправим наклон датчика (2) — PSV 43,3 см/сек; курсив вдоль потока (3) — правильная PSV 86,6 см/сек. RI и PI не требуют коррекции угла.

Количественные характеристики спектра
Vps — пиковая систолическая скорость;
Ved — максимальная конечная диастолическая скорость;
TAMX — усредненная по времени максимальная скорость кровотока;
TAV — усредненная по времени средняя скорость кровотока;
RI=(Vps-Ved)/Vps — индекс резистивности отражает сопротивление потоку далее места измерения;
PI=(Vps-Ved)/TAMX — индекс пульсативности отражает упругоэластические свойства артерий;
В воротной вене PI=PSV/EDV;
PI’=(Vps-Ved)/TAV — модифицированный индекс пульсативности;
SBI=(Vps-TAV)/Vps=1-TAV/Vps — индекc спектрального расширения отражает турбулентность потока;
SBI’=(Vps-TAV)/TAMX — модифицированный индекc спектрального расширения;
S/D — систолодиастолическое соотношение;
AT — время ускорения;
AI — индекс ускорения.
Задача. Измерение пиковая систолическая, максимальная конечная диастолическая скорости, TAMX, TAV для артерий с высоким и низким сопротивлением.
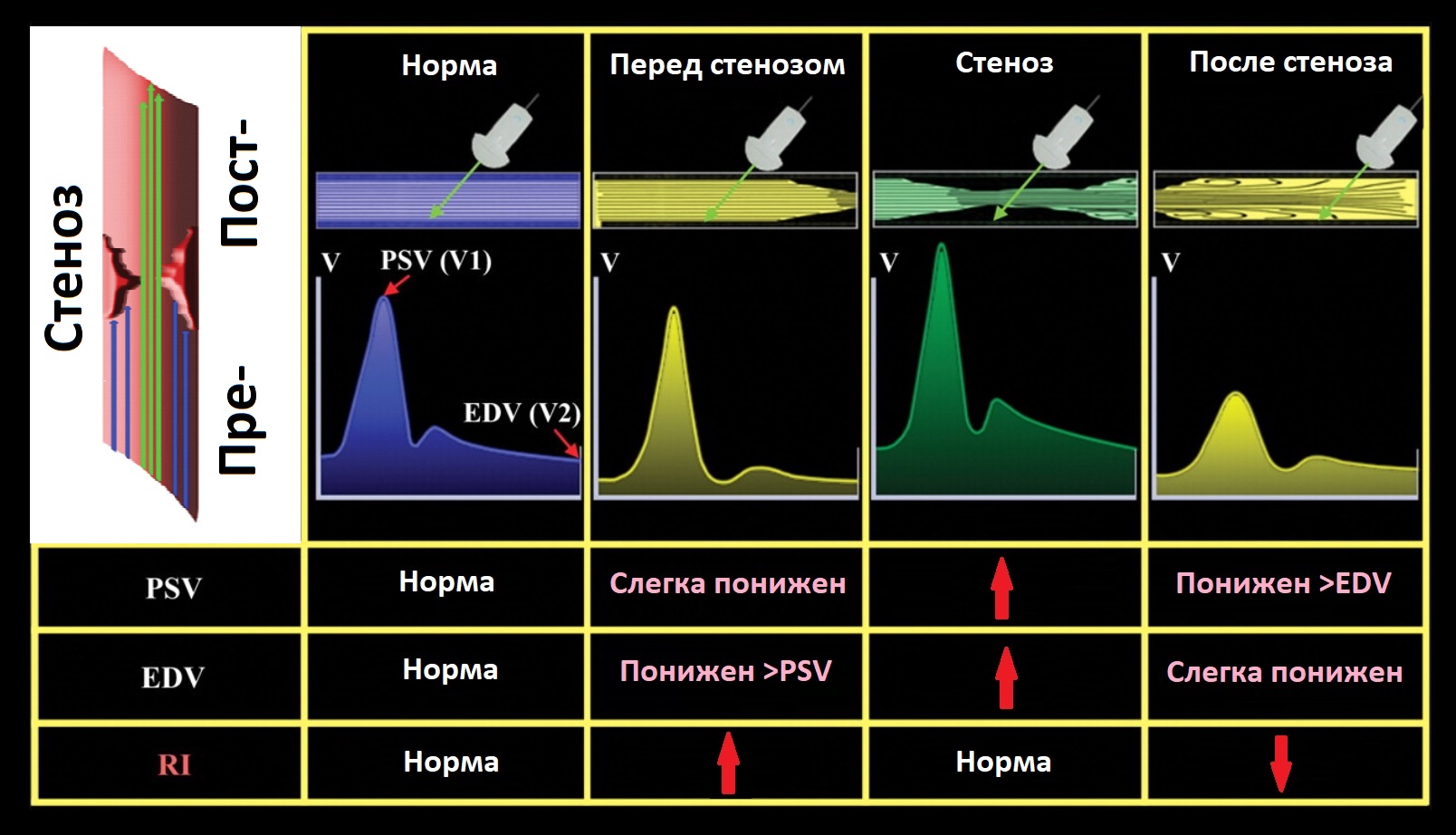
PSV и EDV высокие в месте стеноза; RI растет перед и падает после стеноза. После стеноза спектр имеет форму tardus-parvus: PSV поздняя — ТРТ>70 мс, PSV/TTP<5 м/с²; маленький — PSV и RI.
Качественные характеристики спектра
Антеградный поток правильный относительно системы кровообращения — К сердцу в венах, ОТ сердца в артериях. Ретроградный поток противен естественному.
При ЦДК принято красить в синий вены, в красный артерии. Спектр рисуют ниже базовой линии на венах, выше базовой линии на артериях.
Антеградный поток печеночной вены К сердцу — сосуд синий, спектр ниже базовой линии; печеночной артерии ОТ сердца — сосуд красный, спектр выше базовой линии.

Перепады скорости могут повторяться через равные промежутки времени. Такой поток цикличный, спектр имеет восходящие и нисходящие отрезки.
В каждом цикле четное количество изгибов, в противном случае он никогда не повторится. Каждый изгиб спектра генерирует звуковой сигнал.
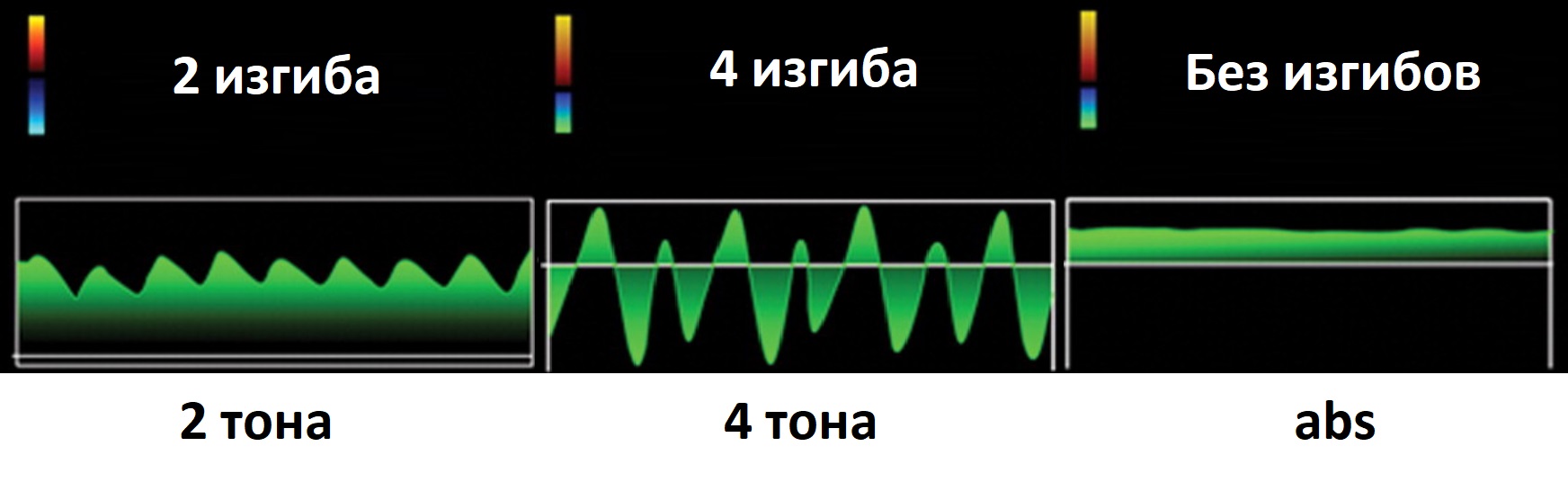
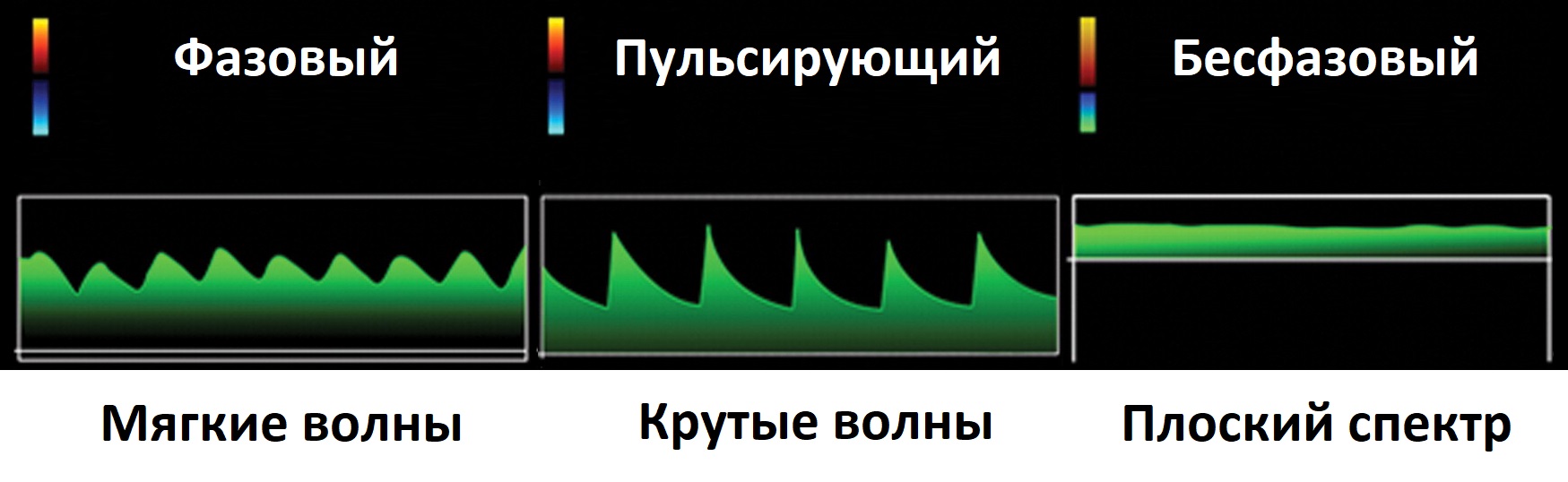
Спектр в венах фазовый — мягкие волны; в артериях пульсирующий — резкие перепады; безфазовый поток с постоянной скоростью.
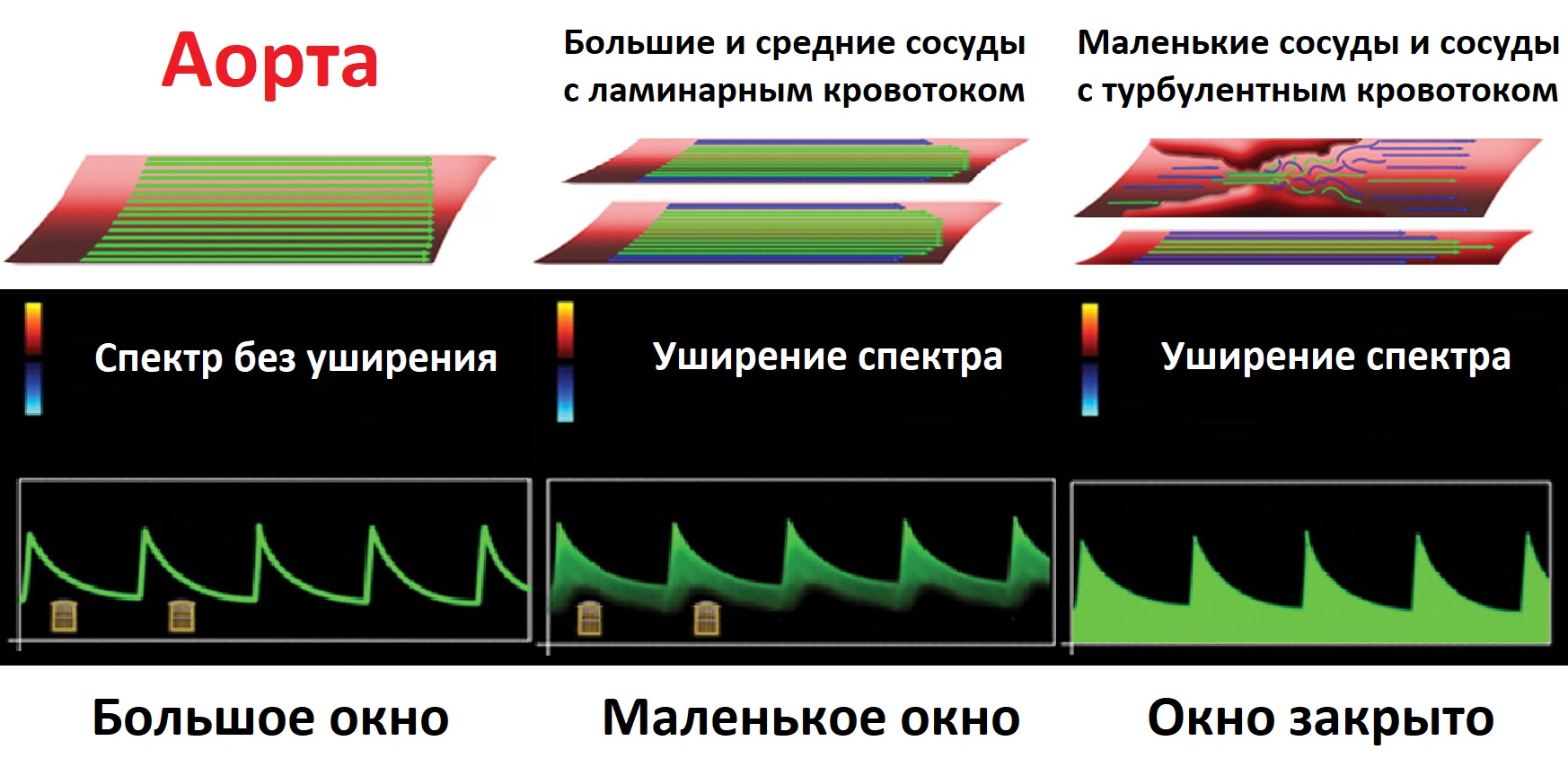
В спектре быстрые эритроциты с большим ΔF ближе к огибающей; медленные эритроциты с маленьким ΔF ближе к базовой линии.
Скорость выше в центре сосуда, ниже у стенки. Когда в ворота попадает большой разброс скоростей, имеется уширение спектра.
В аорте ворота пропускают равномерно движущуюся колонну из кровяных телец — спектр без уширения, большое спектральное окно.
В некрупных сосудах с ламинарным потоком и при турбулентности уширение спектра полностью закрывает спектральное окно.
В сосудах с высоким сопротивлением в конце диастолы поток слабый, RI>0,7; в сосудах с низким сопротивлением в диастолу поток значимый, RI 0,55-0,7.
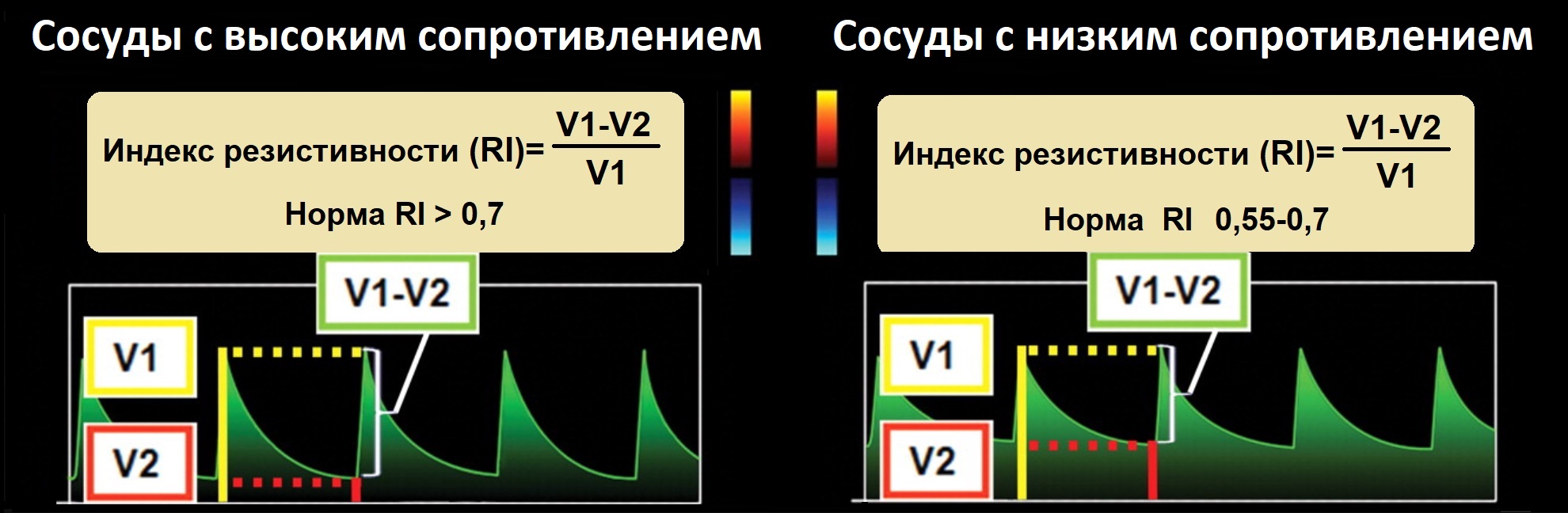
Сосуды с высоким сопротивлением: наружная сонная и артерии конечностей, а так же верхняя и нижняя брыжеечные артерии у голодного.
Сосуды с низким сопротивлением: внутренняя сонная, почечная, печеночная, яичковая артерии, а так же брыжеечные артерии у сытого.
Нормальная форма спектра в сосудах

Аномальная форма спектра в сосудах

Берегите себя, Ваш Диагностер!
Источник