Форма сосуда в ортогональной проекции

Теоретические свойства построения чертежа в инженерной графике базируются на правилах построения изображений, основанных на методе проекций. Изображение объектов трехмерного пространства на плоскости получают методом проецирования.

Проецирование – это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.

Аппарат проецирования включает в себя изображаемые объекты – точки А, В, проецирующие лучи i и плоскость проекции п’, на которой получается изображение объектов. Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А’, т. е. [i ~ A; i ^ п’ = А’]. Проекцией точки В является точка В’, хотя проекция точки В, лежащей в плоскости п’, совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.

В основу построения объекта на плоскости положен метод проекций. Проецирование – это построение объекта на плоскости при помощи проецирующих лучей, исходящих из точки. Плоскость, на которую падают лучи – проецирующая плоскость.

Аппарат проецирования включает в себя:

Пi – плоскость проекций,

S – центр проецирования,

А – объект проецирования (точка),

SA – проецирующую прямую,

Ai – проекцию точки А.

Ортогональное проецирование – это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.

Аппарат такого проецирования состоит из одной плоскости проекций.

Чтобы получить ортогональную проекцию точки А, через неё надо провести проецирующий луч перпендикулярно к П1. Точка А1 называется ортогональной или прямоугольной проекцией точки А.

Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ.

Все свойства параллельного проецирования выполнимы и для ортогонального проецирования. Однако ортогональные проекции обладают ещё некоторыми свойствами.

Свойство ортогонального проецирования:

Для ортогонального проецирования будет справедлива теорема о проецировании прямого угла:

Теорема: Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.

Доказательство:

Дан прямой угол АВС, у которого по условию прямая ВС перепендикулярнаАВ и ВС || плоскости проекций П1. По построению прямая ВС к проецирующему лучу ВВ1. Следовательно, прямая ВС к плоскости b (АВхВВ1), т.к. она к двум пересекающимся прямым , лежащим в этой плоскости. По условию прямая В1С1 || ВС, поэтому тоже к плоскости b, т. е. и прямой А1В1 этой плоскости. Следовательно, угол между прямыми А1В1 и В1С1 равен 90°, что и требовалось доказать.

Ортогональное проецирование обеспечивает простоту геометрических построений при определении ортогональных проекций точек, а так же возможность сохранять на проекциях форму и размеры проецируемой фигуры. Эти достоинства обеспечили ортогональному проецированию широкое применение в техническом черчении.

Рассмотренные методы проецирования позволяют решить прямую задачу начертательной геометрии, т.е. по оригиналу построить плоский чертёж. Полученные таким образом проекции на одну плоскость дают неполное представление о предмете, его форме и положении в пространстве, т.е. такой чертёж не обладает свойством обратимости.

Чтобы получить обратимый чертеж, т.е. чертеж, дающий полное представление о форме, размерах и положении оригинала в пространстве, однокартинный чертеж дополняют. В зависимости от дополнения существуют различные виды чертежей.

В промышленности весьма широко используются так назы­ваемые плоские детали (пластины, уголки, прокладки, решетки, лекала швейного и обувного производств и т. д.), имеющие про­стую или сложную конфигурацию при незначительной толщине самих деталей (рис 1). Для отображения их на чертеже доста­точно построения одной проекции.

Рис. 1. Плоские детали: а — «Пластины»; б — «Уголок», в — «Прокладки»; г — «Решетки»

При прямоугольном проецировании на одну плоскость проекций деталь следует расположить таким образом, чтобы полученное изображение давало наибольшую информацию о ее форме (рис. 2).

Рис. 2. Расположение детали относительно плоскости проекций: а — правильное расположение;
б — неправильное расположение; в — про­цесс и результат проецирования

Выберем для получения изображения вертикальную (фронтальную) плоскость проекций (К). Перед ней мысленно расположим деталь «Уголок» (рис. 2, в) так, чтобы формообразующая грань стала параллельно плоскости проекций. В результате прямоугольного (ортогонального) проецирования получим изображение детали, на котором грани предмета, параллельные плоскости проекций, отобразятся в натуральную величину. Боковые грани, перпендикулярные плоскости проекций, спроецируются в отрезки прямых. Ребра, параллельные фронтальной плоскости проекций, изобразятся в натуральную величину, а ребра, перпендикулярные ей, в точки.

Цилиндрические отверстия «Уголка» спроецируются в виде окружностей. Полученное изображение называется фронтальной проекцией. Эта проекция содержит основную информацию о форме детали, воспроизводит ее контур, дает представление о высоте и длине, не передавая при этом толщину или ширину.

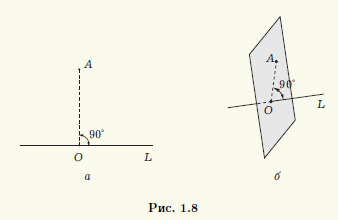
Пусть на плоскости заданы прямая L и точка A. Опустим из точки A на прямую L перпендикуляр (рис. 1.8, а). Тогда его основание (точку O) называют ортогональной проекцией точки A на прямую L. Если прямая L и точка A заданы в пространстве, то в этом случае ортогональной проекцией точки A на прямую L называют точку O пересечения прямой L с перпендикулярной ей плоскостью, проходящей через точку A (рис. 1.8, б). Если точка A лежит на прямой L, то она совпадает со своей ортогональной проекцией на L.

Для вектора – AB (на плоскости или в пространстве) можно построить ортогональные проекции на прямую L его начала и конца (рис. 1.9). Вектор OAOB, соединяющий эти проекции OA и OB и лежащий на прямой L, называют ортогональной проекцией вектора AB на прямую L.

Прямую, на которой задано одно из двух возможных направлений, называют осью. Выбранное направление на оси изображают с помощью стрелки на соответствующем конце оси. Ортогональную проекцию OAOB вектора AB на ось l можно полностью описать длиной вектора OAOB, приписав ей знак,

указывающий направление вектора. Если направление OAOB совпадает с заданным направлением оси, то берут знак плюс, а если направление вектора противоположно направлению оси, то берут знак минус. Длину вектора OAOB со знаком, определяющим направление этого вектора, называют ортогональной проекцией вектора AB на ось l и обозначают прlа.

Обратим внимание на то, что ортогональной проекцией вектора на ось является число, в то время как ортогональная проекция вектора на прямую – это вектор. Чтобы вектору соответствовало число как его проекция, на прямой нужно выбрать одно из двух возможных направлений.

Каждый ненулевой вектор l однозначно определяет ось: его можно рассматривать расположенным на некоторой прямой и задающим на ней направление. Ортогональную проекцию вектора на такую ось называют ортогональной проекцией этого вектора на направление вектора l.

Угол между направлениями двух ненулевых векторов называют углом между этими векторами. Угол может изменяться в пределах от 0 до π. Крайние значения 0 и π отвечают коллинеарным векторам, соответственно однонаправленным и противоположно направленным. Если хотя бы один из двух векторов является нулевым, то угол между такими векторами не определен. Удобно, однако, считать, что в этом случае угол имеет произвольное значение. Так, нулевой вектор коллинеарен любому другому, что формально соответствует углу 0 (или π). Конкретное значение, приписываемое углу между нулевым вектором и каким-либо другим, выбирают исходя из ситуации.

Теорема 1.1. Ортогональная проекция вектора а на направление ненулевого вектора l равна длине |а|, умноженной на косинус угла φ между векторами а и l, т.е.

прl = а|а| cos

где – угол между векторами а и l

◄ Пусть вектор l лежит на прямой L, а его началом является точка A. Совместим начало вектора а с точкой A, и пусть его концом будет точка B (рис. 1.10). Построим ортогональную проекцию C точки B на прямую L. Тогда вектор AC является ортогональной проекцией вектора а = AB на прямую L.

Если угол φ между векторами а и l острый (как это показано на рис. 1.10, а), то конец вектора l и точка C лежат по одну сторону от точки A. В этом случае проекция а на направление вектора l равна длине |AC| = |AB| cosφ катета AC треугольника ABC.

Если угол φ тупой (см. рис. 1.10, б), то конец вектора l и точка C лежат по разные стороны от точки A. Это значит, что векторы AC и l имеют противоположные направления, а проекция вектора а равна – |AC|. В треугольнике ABC угол ψ, прилежащий к катету AC, равен π – φ, поэтому |AC| = |AB| cos( π – φ) = – |AB| cosφ.

Если же φ = π/2 или а = 0, то точка C совпадает с точкой A и вектор AC является нулевым вектором. Однако cosπ/2 = 0, следовательно, и в этом случае утверждение теоремы справедливо. ►

Теорема 1.2. Ортогональная проекция суммы векторов на направление ненулевого вектора равна сумме их ортогональных проекций на направление этого вектора, а при умножении вектора на число его ортогональная проекция на направление ненулевого вектора умножается на то же число:

прl(а + b) = прlа + прlb, прl(λа) – λпрlа.

◄ Доказательство следует из рис. 1.11. В случае, изображенном на рис. 1.11, а, имеем прlа = |AB|, прlb = -|BC|, прl(а + b) = |AC| = |AB| – |BC|. В случае, изображенном на рис. 1.11, б, прlа = |AB| и, если λ > 0, прl(λа) = |AE| = λ|AB|. Остальные варианты (точка C не принадлежит отрезку AB в случае а, λ ≤ 0 в случае б) рассматриваются аналогично. ►