Форма свободной поверхности жидкости во вращающемся сосуде
Сегодня я заварил себе чай и задумался
Сегодня утром я задумался, пока размешивал два кубика сахара в чашке с только что заваренным чаем. Задумался о форме жидкости, которую она принимает при вращении. Безусловно, все представляют себе что будет, если очень быстро начать размешивать сахар в чашке с чаем. Мне захотелось рассмотреть этот банальный и привычный процесс подробнее и попытаться рассказать Вам немного интересного из физики окружающих нас в быту явлений.
Идея эксперимента
Давайте представим, что мы имеем некоторую цилиндрическую тару, в которой находится некоторая жидкость. Вращаться жидкость можно заставить, как минимум, двумя очевидными способами: размешать её каким-нибудь предметом или начать вращать цилиндрическую тару, что, благодаря силам трения между жидкостью и поверхностью сосуда, приведет к вращению жидкости, увлекаемой содержащим её вращающимся сосудам.
Физическая модель
Остановимся на втором варианте. Итак, у нас есть вращающийся с постоянной циклической частотой сосуд, в котором при динамическом равновесии с постоянной циклической частотой вращается жидкость в том же направлении.
Вырежем из всей жидкости элементарный бесконечно малый объем около поверхности и рассмотрим какие силы на него действуют. В силу симметрии задачи, будем ориентироваться на цилиндрические координаты, что заметно упростит расчеты.
Качественный расчет формы поверхности
Запишем второй закон Ньютона для элементарного кусочка объема жидкости:
К примеру, после размешивания ложкой сахара в чашке только что заваренного чая, жидкость вращается вокруг оси симметрии, отсюда наш элементарный кусочек объема имеет центростремительное ускорение. Поэтому спроецируем наш закон Ньютона на ось, совпадающую с радиусом-вектором от элементарного объема до оси симметрии. Не будем учитывать вязкость и поверхностное натяжение. Сила, сообщающая центростремительное ускорение (в правой части нашего закона движения) возникнет из-за разности давлений столбов жидкости, что можно увидеть на увеличенной части первого рисунка.
Таким образом, у нас получится следующее выражение:
, где , а та самая сила определится как , где площадью эффективного сечения обозначена та площадь нашего элементарного объема, на которую действует разница давлений столбов жидкости .
Получаем силу
Масса нашего элемента объема определяется по знакомой всем формуле , а сам объем будет равен (элементарный объем в цилиндрических координатах).
В итоге, 2 закон Ньютона для нашей маленькой задачки расписывается в следующее выражение:
После небольших сокращений и преобразований получаем:
Теперь проинтегрируем обе части выражения, используя неопределенные интегралы:
Детальный расчет формы поверхности
Теперь мы получили вполне ясную зависимость для формы поверхности и с уверенностью можем сказать, что это параболоид. Но нам неизвестна постоянная величина . Давайте её определим для полного понимания физики процесса.
Так как объем жидкости не меняется (мы считаем, что не пролили ни капли, пока размешивали наш чай ツ), то запишем объемы до вращения и во время вращения с постоянной циклической частотой.
До вращения:
, где – это высота жидкости в цилиндрической поверхности в спокойном состоянии (вращения нет).
Во время вращения:
Данные объемы равны, поэтому:
Отсюда выражается ранее неизвестная постоянная:
И окончательное уравнение формы поверхности вращающейся жидкости имеет вид:
или преобразовав
Некоторые заметки
Хотелось бы обратить внимание на то, что форма поверхности зависит от частоты вращения, ускорения свободного падения, геометрических параметров сосуда, первоначального объема жидкости, но не зависит от плотности жидкости. Это выражение мне показалось довольно интересным, так как с его помощью можно легко смоделировать примерное расположение жидкости внутри вращающегося вокруг своей оси симметрии цилиндрического сосуда. Для этого можно воспользоваться MathCAD’ом и построить несколько графиков.
Графическое представление результатов расчета
Возьмем вполне реальные параметры системы, соизмеримые с размерами чашки или стакана.
Радиус цилиндрической поверхности:
Высота жидкости в цилиндрической поверхности без вращения:
Ускорение свободного падения:
Циклическая частота вращения цилиндрической поверхности:
(Все значения этих величин заданы в системе Си)
Далее перепишем нашу функцию для её отображения в MathCAD.
Для 2D отображения сечения:
Для 3D отображения поверхности:
В качестве изменяющегося параметра будем менять циклическую частоту вращения . Результаты можно наблюдать на рисунках ниже:
При циклической частоте
При циклической частоте
При циклической частоте
При циклической частоте
При циклической частоте
При циклической частоте
Выводы
Видно, что если циклическая частота превысит значение , то мы увидим дно вращающегося цилиндрического сосуда, и, начиная с этой частоты, жидкость будет плавно «переходить» на стенки сосуда, всё сильнее оголяя дно. Очевидно, что при очень больших частотах вся жидкость растечется по стенкам сосуда. Теперь мы знаем все параметры такой жидкости. Зная её уравнение, не составит большого труда рассчитать толщину слоя жидкости на стенке сосуда на определенной высоте при определенной частоте.
upd. Отдельно хотелось бы подчеркнуть те противоречащие друг другу допущения, которые были приняты при рассмотрении задачи:
1. Считалось что, жидкость вращается благодаря вращению сосуда, который её содержит. Это может быть только при учете внутреннего трения, вязкости и поверхностного натяжения.
2. Но при выводе формы поверхности эти явления не учитываются для того, чтобы упростить решение и показать только качественный результаты моделирования. Т.е. решение немного противоречит описываемой изначально модели. Учет всех явлений, включая нелинейность процесса при высоких частотах, настолько бы усложнил задачу, что её вряд ли можно было бы решить аналитически и показать примерную и понятную модель для человека, который не связан с математикой/физикой.
3. Цель состоялась в том, чтобы показать лишь очень приближенное и самое простое решение, включающее в себя ряд допущений.
Источник
Определим, какую форму принимает поверхность жидкости в равномерно вращающемся сосуде. Свободная поверхность и здесь будет поверхностью уровня, только на этот раз это будет уже не горизонтальная плоскость, поскольку на жидкость из объемных сил действует не только сила тяжести.
При равномерном вращении сосуда с жидкостью поставленную задачу можно рассматривать как гидростатическую, жидкость будет находиться в покое относительно стенок сосуда, то есть здесь будет наблюдаться случай «относительного покоя». При этом жидкость будет находиться в равновесии под действием двух объемных сил: силы тяжести и силы инерции – центробежной силы. На каждую частицу жидкости во вращающемся сосуде действуют обе эти силы.
Центробежная сила, действующая на частицу жидкости, находящуюся в некоторой произвольной точке М (рис. 2.8), для кругового движения определится по формуле
.
Здесь r – радиус окружности (расстояние от точки до оси вращения), по которой вращается частица жидкости, находящаяся в точке М,
ω – угловая скорость вращения,
m – масса частицы жидкости.
Удельная центробежная сила, то есть сила, отнесенная к единице массы, будет равна
Проекции удельной центробежной силы на оси координат определятся как (рис. 2.8)
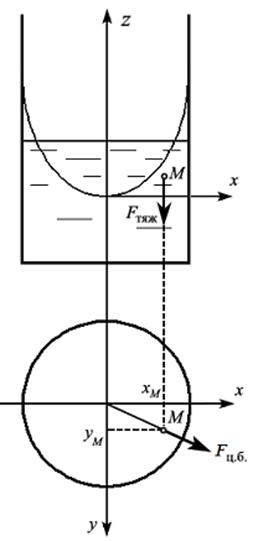
Рис. 2.8
Проекции удельной силы тяжести на оси
Суммарно для проекций удельных объемных сил, действующих на частицу жидкости, получаем
Вспомним дифференциальное уравнение равновесия жидкости:
или
.
Подставим в него значения проекций объемных сил:
Проинтегрируем уравнение, считая ρ величиной постоянной. Имеем
или
Заметим, что при вращении жидких частиц по круговым траекториям
.
Для определения константы интегрирования сформулируем граничные условия. Обратим внимание на то, что при вращении свободная поверхность жидкости примет симметричную вогнутую форму. Расположим начало координат в низшей точке свободной поверхности. На свободной поверхности жидкости давление равно атмосферному.
Тогда граничное условие формулируется так: при x = y = z = 0 давление p = pатм.
Определяя из этого условия константу интегрирования, получим:
const = – pатм.
Уравнение для определения давления примет вид:
| (2.11) |
По этой формуле можно вычислить давление в любой точке внутри объема жидкости, находящейся в сосуде, вращающемся с постоянной угловой скоростью.
Как определить форму свободной поверхности жидкости? Свободная поверхность является поверхностью уровня, то есть поверхностью равного давления. Давление во всех ее точках равно атмосферному p = pатм. Используя это условие, из уравнения (2.11) получаем
,
где индекс «п» относится к координатам точек, находящихся на поверхности жидкости. Окончательно имеем
| (2.12) |
Уравнение (2.12) дает зависимость вертикальной координаты точек, расположенных на свободной поверхности жидкости, от расстояния до оси вращения: . Это и есть уравнение свободной поверхности жидкости, находящейся в равномерно вращающемся сосуде. Видно, что форма свободной поверхности – параболоид вращения с вертикальной осью симметрии.
Источник
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции. Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l) высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r – радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в. Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.11).
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w2r. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Рис. 2.11
Учитывая, что сила j нормальна к свободной поверхности, получим
отсюда
или после интегрирования
В точке пересечения свободной поверхности с осью вращения C = h, поэтому окончательно будем иметь
(2.10)
т. е. свободная поверхность жидкости является параболоидом вращения.
Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.
Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса
или
Рис. 2.12
После интегрирования
Постоянную C найдем из условия, что при r = r0 p = p0.
Следовательно
Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
(2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим
а затем следует выполнить интегрирование в требуемых пределах.
При большой скорости вращения жидкости получается значительная суммарная сила давления на стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.
Источник
Бурлаки Н. Опыты с вращающейся жидкостью //Квант. – 1992. – № 2. – С. 42-46.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Из кувшина вылить можно только то, что было в нем.
Ш. Руставели
Эксперименты с вращающейся жидкостью демонстрируют сложные пространственные движения, порой – очевидные, но необъяснимые, порой – невероятные, но поучительные. Большинство из них можно провести в школьной физической лаборатории или в домашних условиях.
Буря в стакане воды
Почему чаинки собираются в центре стакана после того, как их раскрутили ложкой? Этот вопрос занимал даже Альберта Эйнштейна, которому и приписывают авторство опыта с чаинками. Не исключено, что здесь сработал «эффект громкого имени» и авторство в объяснении ранее известного явления действительно было приписано выдающемуся ученому, но теперь мы не можем с уверенностью сказать, что же было на самом деле. В любом случае объяснение Эйнштейна, опубликованное в 1926 году на страницах журнала «Naturwissenschaften», заслуживает того, чтобы привести его здесь: «Я начну с небольшого эксперимента, который каждый может легко повторить. Представим себе чашку с плоским дном, полную чая. Пусть на дне ее имеется несколько чаинок, которые остаются там, так как оказываются тяжелее вытесняемой ими жидкости. Если с помощью ложки привести во вращение жидкость в чашке, то чаинки быстро соберутся в центре дна сосуда. Объяснение этого явления заключается в следующем… Слои жидкости, находящиеся по соседству со стенками чашки, задерживаются благодаря трению, так что угловая скорость вращения… будет вблизи дна меньше, чем вдали от него. Результатом этого явится круговое движение жидкости, которое возрастает до тех пор, пока под влиянием трения не станет стационарным. Чаинки сносятся в центр круговым движением, что и доказывает его существование».
В своем письме к Эйнштейну один из основоположников квантовой механики Э. Шредингер, называя это объяснение «очаровательным», не удержался от весьма нестандартного комплимента основателю теории относительности: «Случайно, несколько дней тому назад, моя жена расспрашивала меня о «феномене чашки чая», но я не сумел дать разумное объяснение. Она говорит, что теперь никогда не сможет перемешивать чай, не вспоминая Вас».
Но вернемся непосредственно к опыту с чаинками. Хотя точного расчета движения чаинок не имеется, качественные соображения просты. «Мокрые» чаинки, плотность которых больше плотности воды, находятся на дне стакана и поэтому при своем движении испытывают силу трения о стекло. Вращаются они не в центре сосуда, а вблизи него, образуя как бы «пояс астероидов». Ширина «пояса» зависит от степени неоднородности чаинок: чаинки разных размеров и масс вращаются по окружностям разных радиусов. Лишь на заключительной стадии торможения они собираются в центре. Этому способствуют восходящие вблизи оси сосуда токи, показанные на рисунке 1 красными линиями и образующиеся вследствие того, что при уменьшении скорости вращения свободная поверхность L, имевшая форму параболоида вращения, стремится стать снова плоской. Чаинки увлекаются придонным потоком, направленным к оси сосуда.
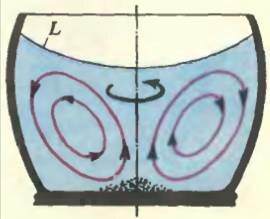
Рис. 1
«Опыт» с чаинками мы проводим каждый день, но не обращаем на их поведение особого внимания. Давайте проведем этот столь хорошо знакомый нам опыт еще раз и попытаемся выяснить, как ведут себя в процессе движения и на его заключительной стадии не только те чаинки, которые находятся на дне стакана, но и те, которые плавают внутри объема и на поверхности воды («сухие» чаинки). Вместо чаинок, можно взять другие частицы, желательно калиброванные. Воду можно раскрутить ложкой, оставляя стакан неподвижным. Возможен и другой способ «закручивания» жидкости – можно раскрутить стакан просто в ладонях (при достаточной ловкости) или поставив его на середину вращающегося диска проигрывателя.
Итак, возможны следующие варианты проведения опыта с чаинками: фиксировать их положение во время вращения или после него, раскручивать чай или стакан и, наконец, наблюдать за придонными, поверхностными или плавающими внутри объема частицами. Всего 2 × 2 × 3 = 12 комбинаций. Впрочем, существует много других вариантов этого на вид простого, а по своей природе чрезвычайно сложного опыта.
Вихри Тейлора
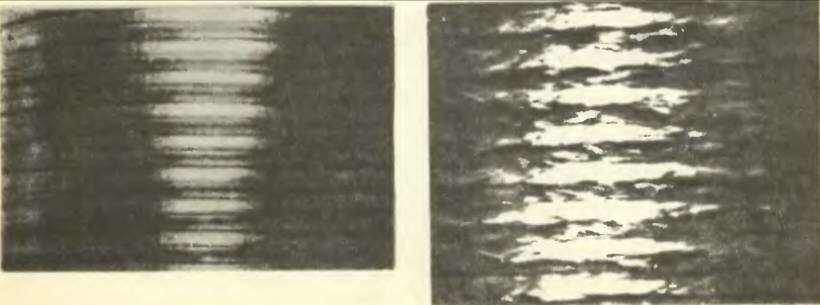
Рис. 2
Не менее интересно наблюдать за поведением жидкости, находящейся между двумя коаксиальными цилиндрами. Течение жидкости, вызванное вращением одного или обоих цилиндров, представляет собой сложное гидродинамическое явление. При малой скорости вращения (малой закрутке) течение в любой горизонтальной плоскости одинаково, т. е. не зависит от вертикальной координаты. С увеличением закрутки возникают так называемые ламинарные (упорядоченные) вихри Тейлора. Фотография вихрей Тейлора при течении машинного масла в зазоре между неподвижным стеклянным и вращающимся металлическим цилиндрами приведена на рисунке 2 слева. Для визуализации течения в масло добавлен алюминиевый порошок. Схема течения дана на рисунке 3, направление движения частиц показано стрелками.
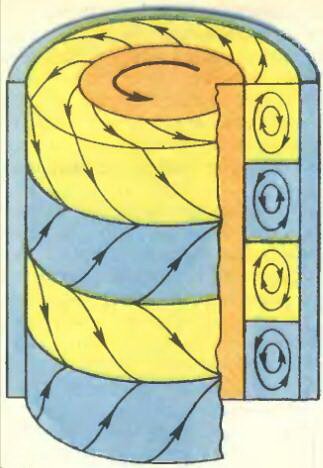
Рис. 3
С дальнейшим ростом скорости вращения появляется периодическое искривление вихрей Тейлора. Наконец, при еще большей скорости на периодическое течение накладывается хаотическое движение (рис. 2, справа). Такие вихри называют турбулентными.
Закрученные потоки
В 1931 году было открыто неожиданное явление, заключающееся в следующем. В специальной камере, имеющей круглое выходное отверстие, закручивают воздух, сжатый до 10 атмосфер. По выходе из отверстия температура воздуха на оси и на периферии оказывается различной. Если на периферии воздух комнатной температуры, то на оси его температура падает до минус 200 градусов Цельсия! Это явление называется эффектом Ранка. В настоящее время природа этого явления до конца не выяснена, хотя исследованию эффекта Ранка посвящается много работ, созываются специальные симпозиумы. Поиск продолжается…
Поскольку эффект Ранка в условиях школьной лаборатории наблюдать нельзя, так как для его осуществления нужна специальная камера, проведем эксперимент, легко воспроизводимый даже в домашних условиях и чем-то напоминающий опыт Ранка. Этот опыт демонстрирует взаимодействие вращательного и поступательного движений жидкости, вытекающей из вращающегося сосуда (рис. 4).
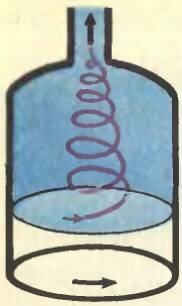
Рис. 4
Предлагаемый эксперимент можно поставить следующим образом. Сосуд с водой укрепите на подшипниках так, чтобы он мог свободно вращаться вокруг своей оси, раскрутите его, а затем снимите крутящие усилия и одновременно откройте сток в дне. После этого скорость вращения сосуда начнет заметно возрастать.
Форма свободной поверхности в этом опыте зависит от скорости вращения и от высоты жидкости Н в сосуде. Если скорость вращения мала или велико значение Н, на свободной поверхности образуется небольшая впадина (рис. 5). С увеличением скорости вращения или с уменьшением H вихрь достигает дна сосуда, а затем проникает в вытекающую из отверстия струю. Подобные воронки можно наблюдать в реках, при спуске воды в ванной.
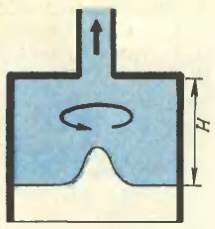
Рис. 5
Взрыв вихря
В 1957 году американские ученые Пекхем и Аткинс обнаружили необычное явление – внезапное разрушение спиральных вихрей (взрыв вихря), сходящих с боковых кромок самолетного крыла. Наблюдать этот необычный эффект можно только в условиях научно-исследовательской лаборатории, поэтому мы лишь расскажем об этом интересном явлении и приведем его фотографии. Модель треугольного крыла самолета устанавливают в потоке жидкости (или воздуха) под некоторым углом к направлению течения. С нижней плоскости крыла частицы жидкости устремляются на верхнюю, где давление меньше, и движутся по потоку вдоль крыла, образуя отходящие от его боковых кромок спиральные вихри. Почти прямые оси вихрей (визуализированные с помощью впрыскиваемой вблизи вершины крыла жидкой краски) искривляются, обретая нерегулярную форму (рис. 6).

Рис. 6
Это во многом загадочное явление изучают в специальных вихревых камерах, где поток воды закручивается искусственным образом, например лопастями вентилятора (в данном случае модель крыла отсутствует), а по оси камеры вводится краска. При малой скорости вращения потока образуется спиральная структура, фотография которой показана на рисунке 7 вверху; при большой скорости осевая линия приобретает «пузыревидную» форму (рис. 7, внизу). Таковы два основных типа взрыва вихря.

Рис. 7
Наблюдение пророчицы Деборы
Не только в опытах с вращающейся жидкостью, но и в любых других ситуациях, где проявляется влияние вязкости, следует различать два типа жидкостей: ньютонову и неньютонову.
Жидкости и газы, состоящие из «легких» молекул с относительными молекулярными массами не более 1000, называют ньютоновыми. К ним относятся воздух и вода при наших земных условиях. Классическая гидродинамика описывает движение ньютоновой жидкости.
«Тяжелые» жидкости – неньютоновы – состоят из огромных молекул, каждая из которых представляет собой цепь из большого числа повторяющихся звеньев. Примером являются полимерные жидкости, молекулярная масса которых 105 – 108: растворы синтетических и биологических полимеров и неразбавленные полимеры, называемые «расплавами». Сюда относятся полиэтилен (-СН2-)n, полистирол (-СН2-СH(С6H5)-)n, натуральный каучук (-СН2-С(СН3)=СН-СН2-)n и т. д. (Здесь n – очень большое число порядка 103 – 106.)
Неньютоновы жидкости обладают рядом особенностей. Например, они имеют память. Дело в том, что время, характерное для процесса перестройки длинных молекул, может превышать время наблюдения за течением жидкости. Течение не успевает перестроиться, имеет место эффект запаздывания, а значит, эффект памяти.
Как утверждает библейская мифология, пророчица Дебора изрекла, что пред Богом текут даже горы. Она первая подметила аналогию между поведением жидких и твердых тел. Но что самое важное – Дебора ясно выразила идею разных временных масштабов. За время своей жизни человек не заметит уменьшения горы – оно незначительно. А по временной шкале Бога горы текут! Ученые часто шутят – юмор помогает им в трудной работе. Числом Деборы они назвали отношение характерного времени «настройки» молекул к времени наблюдения. Когда число Деборы велико, жидкость ведет себя подобно твердому телу. При малых числах Деборы жидкость ведет себя как ньютонова. В промежуточном случае, когда число Деборы порядка 1, жидкость обладает рядом аномальных свойств.
Удивительные свойства неньютоновых жидкостей
Двигаясь в трубе, жидкость испытывает силу трения о ее поверхность, в результате чего кинетическая энергия переходит в тепловую. Поэтому снижение силы трения является важной технической проблемой. Как оказалось, добавление в жидкость малого количества полимера значительно снижает силу трения. Это удивительное и до конца не понятое явление называется эффектом Томса. Всего лишь 20 миллионных долей полиокса (длинноцепочного полимера) могут снизить силу трения турбулентного потока в трубе на 50 %!
В 50-е годы американские пожарные начали добавлять полимерные добавки в жидкость, вытекающую из брандспойта, при этом длина струи увеличивалась в полтора раза. Полимерные добавки в смазывающих, материалах повышают ресурсы станков и приборов. Можно увеличивать скорость судна путем впрыскивания вблизи его носовой части малых количеств полимерного раствора. Имеется гипотеза, что дельфины и другие обитатели морей и океанов тоже «используют» эффект Томса для уменьшения гидродинамического сопротивления.
Теперь, подготовленные к неожиданностям, снова перейдем к теме нашей беседы – опытам с вращающейся жидкостью. Сравним, как поведут себя ньютоновы и неньютоновы жидкости; оказавшись в одинаковых условиях. В наших опытах в качестве ньютоновой жидкости можно использовать воду, а неньютоновой – подсолнечное масло.
Вставьте во вращающийся стакан с водой неподвижный стержень, ось которого совпадает с осью стакана. Свободная поверхность не утратит форму параболоида вращения. Если же вместо воды взять подсолнечное масло, то жидкость поднимется в центре стакана. Свободная поверхность уже не будет параболоидом. Опыт можно изменить: вращать не стакан, а стержень. Эффект будет тот же самый. Подобная картина возникает, если убрать стержень, а на дно стакана поместить вращающийся диск. Свободная поверхность ньютоновой жидкости в центре опускается, неньютоновой – поднимается.
Если вращающийся диск разместить на поверхности жидкости, то наряду с первичным потоком, скорость которого направлена по касательной к диску, возникнет вторичный поток в меридиональном направлении (красные линии на рисунке 8). В ньютоновой (а) и неньютоновой (б) жидкостях направления вторичного течения противоположны.
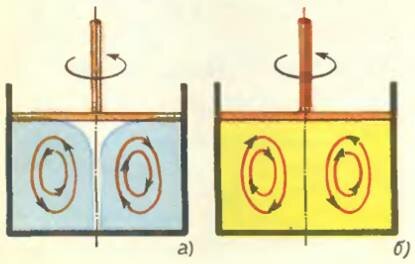
Рис. 8
Источник
