Формула давления на дно цилиндрического сосуда

Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.
Опыт
Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.
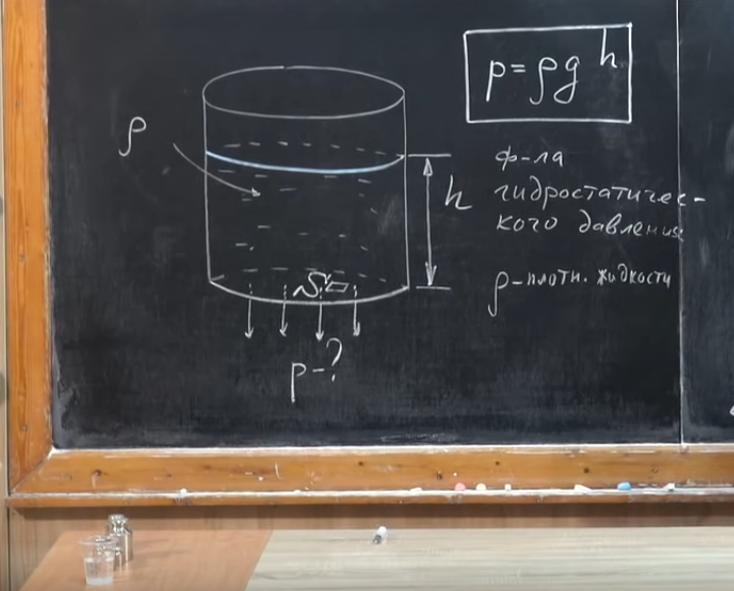
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).
Расчет давления жидкости на дно сосуда
Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.
Давление, которое жидкость создает на дно сосуда, называется гидростатическим. “Гидро” — это “вода”, а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.
Давление в толще жидкости
Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.

Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.
Давление в наклонном сосуде
Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.
Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.
А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1< P2. Как же тогда рассчитать давление жидкости на дно и стенки сосуда в трубке, которая расположена под наклоном?
Высота столба жидкости и давление
Чтобы это выяснить, проведем следующий мысленный эксперимент. Возьмем сосуд, наполненный жидкостью. Поместим в него две трубки из металлической сетки. Одну расположим вертикально, а другую – наклонно, таким образом, что ее нижний конец будет находиться на той же глубине, что и дно первой трубки. Поскольку емкости находятся на одинаковой глубине h, то давление жидкости на дно и стенки сосуда будет тоже одинаковым.

Теперь заделаем все отверстия в трубках. Из-за того, что они стали сплошными, давление в их нижних частях изменится? Нет. Хотя давление и одинаково, а сосуды равны по размеру, масса жидкости в вертикальной трубке меньше. Глубина, на которой находится нижняя часть трубки, называется высотой столба жидкости. Дадим определение данному понятию: это отсчитываемое по вертикали расстояние от свободной поверхности до данной точки жидкости. В нашем примере высота столба жидкости одинакова, поэтому и давление одинаково. В предыдущем опыте высота столба жидкости в правой трубке больше, чем в левой. Поэтому давление P1 меньше, чем P2.
Источник
Возьмем
цилиндрический сосуд с горизонтальным дном и вертикальными стенками,
наполненный жидкостью до высоты (рис. 248).
Рис. 248. В
сосуде с вертикальными стенками сила давления на дно равна весу всей налитой
жидкости
Рис. 249. Во
всех изображенных сосудах сила давления на дно одинакова. В первых двух сосудах
она больше веса налитой жидкости, в двух других — меньше
Гидростатическое
давление в каждой точке дна сосуда будет одно и то же:
.
Если
дно сосуда имеет площадь , то сила давления жидкости на дно
сосуда ,
т. е. равна весу жидкости, налитой в сосуд.
Рассмотрим
теперь сосуды, отличающиеся по форме, но с одинаковой площадью дна (рис. 249).
Если жидкость в каждом из них налита до одной и той же высоты , то давление на
дно . во
всех сосудах одно и то же. Следовательно, сила давления на дно, равная
,
также
одинакова во всех сосудах. Она равна весу столба жидкости с основанием, равным
площади дна сосуда, и высотой, равной высоте налитой жидкости. На рис. 249 этот
столб показан около каждого сосуда штриховыми линиями. Обратите внимание на то,
что сила давления на дно не зависит от формы сосуда и может быть как больше,
так и меньше веса налитой жидкости.
Рис. 250.
Прибор Паскаля с набором сосудов. Сечения одинаковы у всех сосудов
Рис. 251.
Опыт с бочкой Паскаля
Этот
вывод можно проверить на опыте при помощи прибора, предложенного Паскалем (рис.
250). На подставке можно закреплять сосуды различной формы, не имеющие дна.
Вместо дна снизу к сосуду плотно прижимается подвешенная к коромыслу весов
пластинка. При наличии жидкости в сосуде на пластинку действует сила давления,
которая отрывает пластинку, когда сила давления начнет превосходить вес гири,
стоящей на другой чашке весов.
У
сосуда с вертикальными стенками (цилиндрический сосуд) дно открывается, когда
вес налитой жидкости достигает веса гири. У сосудов другой формы дно
открывается при той же самой высоте столба жидкости, хотя вес налитой воды
может быть и больше (расширяющийся кверху сосуд), и меньше (суживающийся сосуд)
веса гири.
Этот
опыт приводит к мысли, что при надлежащей форме сосуда можно с помощью
небольшого количества воды получить огромные силы давления на дно. Паскаль
присоединил к плотно законопаченной бочке, налитой водой, длинную тонкую
вертикальную трубку (рис. 251). Когда трубку заполняют водой, сила
гидростатического давления на дно становится равной весу столба воды, площадь
основания которого равна площади дна бочки, а высота равна высоте трубки.
Соответственно увеличиваются и силы давления на стенки и верхнее днище бочки.
Когда Паскаль заполнил трубку до высоты в несколько метров, для чего потребовалось
лишь несколько кружек воды, возникшие силы давления разорвали бочку.
Как
объяснить, что сила давления на дно сосуда может быть, в зависимости от формы
сосуда, больше или меньше веса жидкости, содержащейся в сосуде? Ведь сила,
действующая со стороны сосуда на жидкость, должна уравновешивать вес жидкости.
Дело в том, что на жидкость в сосуде действует не только дно, но и стенки
сосуда. В расширяющемся кверху сосуде силы, с которыми стенки действуют на
жидкость, имеют составляющие, направленные вверх: таким образом, часть веса
жидкости уравновешивается силами давления стенок и только часть должна быть
уравновешена силами давления со стороны дна. Наоборот, в суживающемся кверху
сосуде дно действует на жидкость вверх, а стенки — вниз; поэтому сила давления
на дно оказывается больше веса жидкости. Сумма же сил, действующих на жидкость
со стороны дна сосуда и его стенок, всегда равна весу жидкости. Рис. 252
наглядно показывает распределение сил, действующих со стороны стенок на
жидкость в сосудах различной формы.
Рис. 252.
Силы, действующие на жидкость со стороны стенок в сосудах различной формы
Рис. 253. При
наливании воды в воронку цилиндр поднимается вверх.
В
суживающемся кверху сосуде со стороны жидкости на стенки действует сила,
направленная вверх. Если стенки такого сосуда сделать подвижными, то жидкость
поднимет их. Такой опыт можно произвести на следующем приборе: поршень
неподвижно закреплен, и на него надет цилиндр, переходящий в вертикальную
трубку (рис. 253). Когда пространство над поршнем заполняется водой, силы
давления на участках и стенок цилиндра поднимают цилиндр
вверх.
Источник
Физика
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление .
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
где ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
F гидр = p гидр S = ρ 0 ghS ,
где p гидр — гидростатическое давление на дно сосуда; ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
где ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
F гидр = p гидр S = ρ 0 g h 2 S ,
где p гидр — гидростатическое давление на дно сосуда; ρ ж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
При расчете давления на дно открытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
где p атм — атмосферное давление; ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Сила давления на дно открытого водоема определяется произведением:
F = pS = ( p атм + ρ 0 gh ) S ,
где S — площадь дна водоема.
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
где ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h 1 — высота столба жидкости при вертикальном положении мензурки; h 2 = h 1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см 3 . Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение . Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
где 〈 p 〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
где ρ 0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
где 2π r — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈 p 〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈 F гидр 〉 = π ρ 0 g R h 2 .
Расчет дает значение:
〈 F гидр 〉 = π ⋅ 2,5 ⋅ 10 3 ⋅ 10 ⋅ 10 ⋅ 10 − 2 ⋅ ( 30 ⋅ 10 − 2 ) 2 ≈ 707 Н ≈ 0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см 3 . Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение . Давление в открытом водоеме определяется формулой
где p атм — атмосферное давление; ρ 0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
Подстановка указанного значения в исходную формулу дает:
4 p атм = p атм + ρ 0 gh ,
Выразим отсюда искомую глубину водоема
и произведем вычисление:
h = 3 ⋅ 100 ⋅ 10 3 1,0 ⋅ 10 3 ⋅ 10 = 30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Формула давления на дно цилиндрического сосуда
Возьмем цилиндрический сосуд с горизонтальным дном и вертикальными стенками, наполненный жидкостью до высоты
(рис. 248).
Рис. 248. В сосуде с вертикальными стенками сила давления на дно равна весу всей налитой жидкости
Рис. 249. Во всех изображенных сосудах сила давления на дно одинакова. В первых двух сосудах она больше веса налитой жидкости, в двух других — меньше
Гидростатическое давление в каждой точке дна сосуда будет одно и то же:
.
Если дно сосуда имеет площадь
, то сила давления жидкости на дно сосуда , т. е. равна весу жидкости, налитой в сосуд.
Рассмотрим теперь сосуды, отличающиеся по форме, но с одинаковой площадью дна (рис. 249). Если жидкость в каждом из них налита до одной и той же высоты
, то давление на дно . во всех сосудах одно и то же. Следовательно, сила давления на дно, равная
,
также одинакова во всех сосудах. Она равна весу столба жидкости с основанием, равным площади дна сосуда, и высотой, равной высоте налитой жидкости. На рис. 249 этот столб показан около каждого сосуда штриховыми линиями. Обратите внимание на то, что сила давления на дно не зависит от формы сосуда и может быть как больше, так и меньше веса налитой жидкости.
Рис. 250. Прибор Паскаля с набором сосудов. Сечения
одинаковы у всех сосудов
Рис. 251. Опыт с бочкой Паскаля
Этот вывод можно проверить на опыте при помощи прибора, предложенного Паскалем (рис. 250). На подставке можно закреплять сосуды различной формы, не имеющие дна. Вместо дна снизу к сосуду плотно прижимается подвешенная к коромыслу весов пластинка. При наличии жидкости в сосуде на пластинку действует сила давления, которая отрывает пластинку, когда сила давления начнет превосходить вес гири, стоящей на другой чашке весов.
У сосуда с вертикальными стенками (цилиндрический сосуд) дно открывается, когда вес налитой жидкости достигает веса гири. У сосудов другой формы дно открывается при той же самой высоте столба жидкости, хотя вес налитой воды может быть и больше (расширяющийся кверху сосуд), и меньше (суживающийся сосуд) веса гири.
Этот опыт приводит к мысли, что при надлежащей форме сосуда можно с помощью небольшого количества воды получить огромные силы давления на дно. Паскаль присоединил к плотно законопаченной бочке, налитой водой, длинную тонкую вертикальную трубку (рис. 251). Когда трубку заполняют водой, сила гидростатического давления на дно становится равной весу столба воды, площадь основания которого равна площади дна бочки, а высота равна высоте трубки. Соответственно увеличиваются и силы давления на стенки и верхнее днище бочки. Когда Паскаль заполнил трубку до высоты в несколько метров, для чего потребовалось лишь несколько кружек воды, возникшие силы давления разорвали бочку.
Как объяснить, что сила давления на дно сосуда может быть, в зависимости от формы сосуда, больше или меньше веса жидкости, содержащейся в сосуде? Ведь сила, действующая со стороны сосуда на жидкость, должна уравновешивать вес жидкости. Дело в том, что на жидкость в сосуде действует не только дно, но и стенки сосуда. В расширяющемся кверху сосуде силы, с которыми стенки действуют на жидкость, имеют составляющие, направленные вверх: таким образом, часть веса жидкости уравновешивается силами давления стенок и только часть должна быть уравновешена силами давления со стороны дна. Наоборот, в суживающемся кверху сосуде дно действует на жидкость вверх, а стенки — вниз; поэтому сила давления на дно оказывается больше веса жидкости. Сумма же сил, действующих на жидкость со стороны дна сосуда и его стенок, всегда равна весу жидкости. Рис. 252 наглядно показывает распределение сил, действующих со стороны стенок на жидкость в сосудах различной формы.
Рис. 252. Силы, действующие на жидкость со стороны стенок в сосудах различной формы
Рис. 253. При наливании воды в воронку цилиндр поднимается вверх.
В суживающемся кверху сосуде со стороны жидкости на стенки действует сила, направленная вверх. Если стенки такого сосуда сделать подвижными, то жидкость поднимет их. Такой опыт можно произвести на следующем приборе: поршень неподвижно закреплен, и на него надет цилиндр, переходящий в вертикальную трубку (рис. 253). Когда пространство над поршнем заполняется водой, силы давления на участках
и стенок цилиндра поднимают цилиндр вверх.
Источник
Давление жидкости на дно и стенки сосуда. Формула гидростатического давления
Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.
Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).
Расчет давления жидкости на дно сосуда
Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.
Давление, которое жидкость создает на дно сосуда, называется гидростатическим. «Гидро» — это «вода», а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.
Давление в толще жидкости
Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.
Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.
Давление в наклонном сосуде
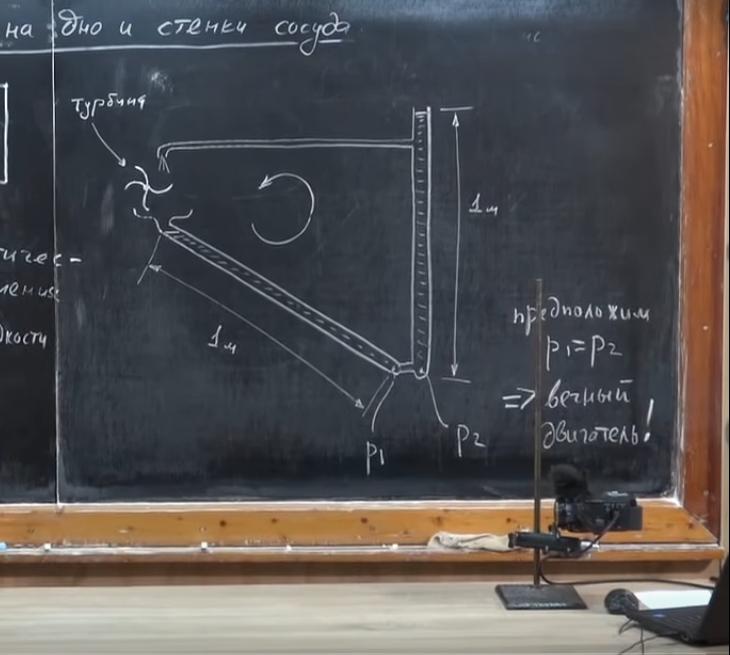
Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.
Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.
А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1 28 марта, 2019
Источник
Источник
