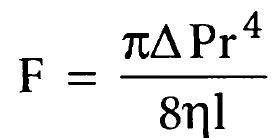Формула гидравлического сопротивления сосудов
Физические основы гемодинамики.
Гемодинамикойназывают область биомеханики, в которой исследуется движение крови по сосудистой системе. Основная задача гемодинамики – установить взаимосвязь между основными гемодинамическими показателями, а также их зависимость от физических параметров крови и кровеносных сосудов. Физической основой гемодинамики является гидродинамика. Течение крови зависит как от свойств крови, так и от свойств кровеносных сосудов. К основным гемодинамическим показателям относятся давление и скорость кровотока. Давление – это сила, действующая со стороны крови на сосуды, приходящаяся на единицу площади: Р = F/S. Различают объемную и линейную скорость кровотока. Объемной скоростью Q называют величину, численно равную объему жидкости, протекающему в единицу времени через данное сечение трубы : Q = V/ t [м3 / с]. Линейная скорость представляет путь, проходимый частицами в единицу времени: V = l / t [м / с]. Линейная скорость и объемная связаны простым соотношением: Q = V·S. Так как жидкость несжимаема, то через любое сечение трубы в единицу времени протекают одинаковые объемы жидкости:
Сердечно-сосудистую систему можно представить в виде замкнутой, многократно разветвленной и заполненной кровью системы трубок с эластичными стенками. Движение крови осуществляется благодаря ритмическим сокращениям сердца.
Количество крови Q, протекающее через поперечное сечение участка сосудистой системы в единицу времени и называемое объемной скоростью кровотока, зависит от разности давлений в начале и конце участка и его сопротивления току крови.
Сопротивление току крови, а следовательно и падение давления на различных участках сосудистой системы весьма различны. Оно зависит от общего просвета и числа сосудов в разветвлении. Наибольшее падение давления крови – не менее 50% от начального давления – происходит в артериолах. Число артериол в сотни раз больше числа крупных артерий при сравнительно небольшом увеличении общего просвета сосудов. Поэтому потери давления от пристеночного трения в них весьма велики. Общее число капилляров еще больше, однако длина их настолько мала, что падение давления крови в них хотя и существенно, но меньше, чем в артериолах.
В сети венозных сосудов, площадь сечения которых в среднем в два раза больше площади сечения соответствующих артерий, скорость течения крови невысока и падения давления незначительны. В крупных венах около сердца давление становится на несколько миллиметров ртутного столба ниже атмосферного. Кровь в этих условиях движется под влиянием присасывающего действия грудной клетки при вдохе.
Течение крови в сосудистой системе в нормальных условиях имеет ламинарный характер. Оно может переходить в турбулентное при нарушении этих условий, например, при резком сужении просвета сосудов. Подобные явления могут иметь место при неполном открытии или, наоборот, при неполном закрытии сердечных или аортальных клапанов.
39. Гидравлическое сопротивление сосудов. Гидравлическое сопротивление разветвлённых участков.
Гидравлическое сопротивление сосудов X = 8 l h /(pR4), где l — длина сосуда, R — его радиус, h — коэффициент вязкости, вводится на основании аналогий законов Ома и Пуазейля (движение электричества и жидкости описываются общими соотношениями).
Аналогия между электрическим и гидравлическим сопротивлениями позволяет использовать правило нахождения электрического сопротивления последовательного и параллельного соединений проводника, для определения гидравлического сопротивления системы последовательно или параллельно соединенных сосудов. Так, например, общее гидравлическое сопротивление последовательно и параллельно соединенных сосудов находится по формулам:
Х = Х1 + Х2 + Х3 + … + ХN
X = (1/X1 + 1/X2 + 1/X3 + …+ 1/XN)-1
Источник
Уравнение
Пуазёйля — закон,
определяющий расход жидкости при
установившемся течении вязкой несжимаемой
жидкости в тонкой цилиндрической трубе
круглого сечения.
Согласно
закону, секундный объёмный расход
жидкости пропорционален перепаду
давления на единицу длины трубки
(градиентудавления
в трубе) и четвёртой степени радиуса
(диаметра) трубы:
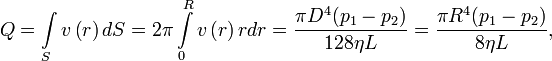
Где
Q — объемный секундный расход жидкости;
R — радиус трубопровода; p1-p2— перепад
давлений на трубке; n—коэффициент
трения; L— длина трубки.
Закон
Пуазёйля работает только при ламинарном
течениии при условии, что длина
трубки превышает так называемую длину
начального участка, необходимую для
развитияламинарного
теченияв трубке.
Гидравлическое
сопротивление прямо
пропорционально длине сосуда и вязкости
крови и обратно пропорционально радиусу
сосуда в 4-й степени, то есть больше всего
зависит от просвета сосуда
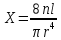
, а также от
состояния стенок сосудов и от их
эластичности.
Так как наибольшим
сопротивлением обладаютартериолы,общее
периферическое сопротивление
сосудов(ОПСС)зависит
главным образом от их тонуса.Различают центральные механизмы
регуляции тонуса артериол (нервные
и гормональные влияния) и местные
(миогенная , метаболическая
и эндотелиальная регуляция).
На артериолы оказывают
постоянный тонический сосудосуживающий
эффектсимпатические
нервы. Основные
гормоны, в норме участвующие в регуляции
тонуса артериол, – этоадреналини
норадреналин.
Миогенная
регуляция сводится к сокращению или
расслаблению гладких мышц сосудов в
ответ на изменения трансмурального
давления; при этом напряжение в их стенке
остается постоянным. Тем самым
обеспечивается ауторегуляция местного
кровотока – постоянство кровотока при
меняющемся перфузионном давлении.
Метаболическая регуляция
обеспечивает расширение сосудов
приповышении
основного обмена(за счет
выбросааденозинаипростагландинов)
игипоксии(также
за счет выделения простагландинов).
7. Законы движения жидкости. Уравнение неразрывности; его связь с особенностями системы капилляров. Уравнение Бернулли; его связь с кровоснабжением мозга и нижних конечностей.
Для движения жидкости по
сосудам необходима энергия, создающая
давление.Жидкость двигается из мест
с большим давлением в места с меньшим
давлением.Скорость течения жидкости
зависит от суммарного поперечного
сечения сосудов.Чем меньше суммарное
поперечное движение сосудов, тем больше
скорость течения жидкости.Один и тот же объем жидкости
проходит с большей скоростью более
узкие участки, чем более широкие.
Следствим
несжимаемости жидкости является ее
свойство: чем уже русло, тем больше
скорсть
течения. Это свойство описывается:
Уравнением
неразрывности: S1V1
= S2V2,
или SV=Const
Здесь S-площадь
поперечного сечения потока,V-средняя
скорость жидкости в этом сечении.
В
спокойном состоянии человека скорость
кровотока в аорте – порядка
V1=0,4м/с.Скорость
в капиллярах- V2=0,5
мм/c.Разница
значений примерно в 800 раз. Следовательно,
если площадь сечения аорты S1=4см2,то
общая площадь поперечных сечений
капилляров большого и малого кругов
кровообращения составляет S2=3200см2.
Оценим
степень ветвления общего потока крови
в системе капилляров.Диаметр капилляра
d=10мкм=10
-3
см. Следовательно,площадь его сечения
S=пd
2/4=0,78*10см
2.
Таким образом,кровь из аорты разветвляется
в системе капилляров на N=S2/s=3,2*103/0,78*10
-6=4,1*10
9
штук.
Уравнение Бернуллисоответствует
закону сохранения механической энергии
при движении жидкости или газа и верно
в той степени, в которой потери на трение
малы. Оно имеет следующий вид: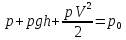
=const
Здесь p0– полное
давление. Величинаp–
это давление, которое поток оказывает
на стенки; его называют статическим
давлением. СлагаемоеpV2/2
называется динамическим давлением.Слагаемоеpghсоответствует
тому вкладу в общее давлениеp0,
которое создается участками потока,
приподнятыми на высотуh,
если таковые имеются.p-
плотность жидкости;V–
ее скорость.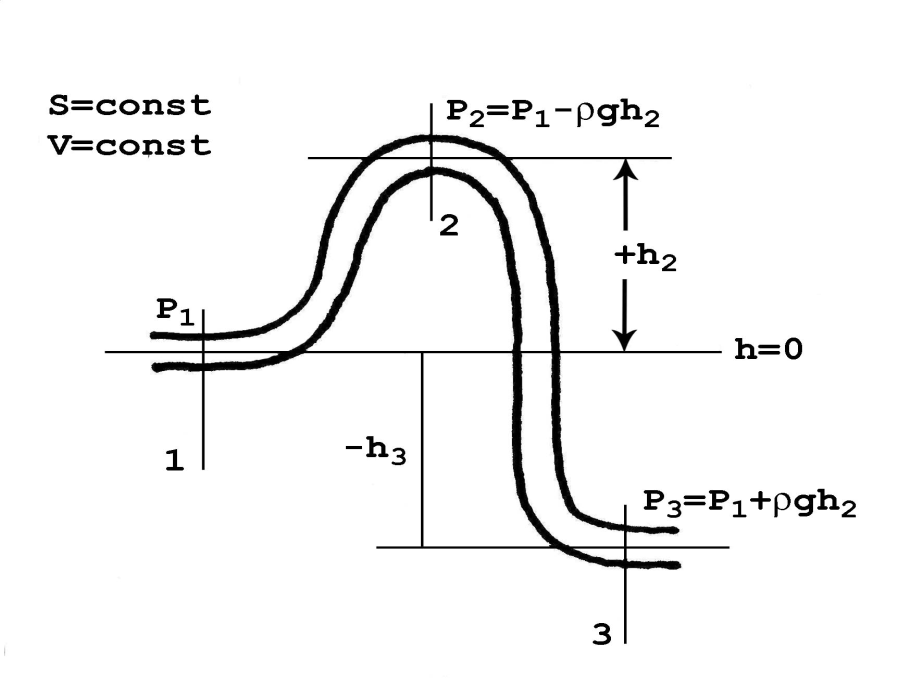
статическое давление в приподнятых
участках: p2 <p1,
а в опущенных – наоборот,p3
>p1.
Применительно
к системе кровообращения, если p1– давление, создаваемое сердцем,
работающим на высотеh=
0, то все, что находится выше этого уровня,
имеет пониженное давление (а это,в
частности, мозг), а все, что ниже (ноги,например) – давление выше, чем то, которое
создает работающее сердце. Для мозга
слагаемоеpghимеет величину
порядка –30 мм рт. столба, а для ног –
порядка +110 мм рт. столба. Система
кровообращения имеет механизмы
регулирования, вносящие поправки на
снабжение кровью органов, находящихся
в неравных условиях.
_______________________________________________________________________________________
Соседние файлы в предмете Медицинская физика
- #
- #
- #
- #
- #
Источник
Закон Пуазейля. Диаметр артериол и их сопротивлениеПричину такого значительного возрастания объемного кровотока при увеличении диаметра сосуда можно объяснить с помощью схемы, представленной на рисунке. На схеме показано поперечное сечение крупного и мелкого кровеносных сосудов. Концентрические слои внутри сосудов указывают на то, что скорость движения каждого слоя отличается от скорости соседних слоев, т.к. происходит ламинарное течение крови (см. ранее в данной главе). Дело в том, что слой крови, прилежащий к стенке сосуда, едва движется благодаря взаимодействию крови и эндотелия сосудистой стенки. Следующий слой крови скользит относительно пристеночного слоя и поэтому движется быстрее. Третий, четвертый, пятый и шестой слои также текут с нарастающей скоростью. Таким образом, пристеночный слой крови движется чрезвычайно медленно, в то время как по продольной оси сосуда кровь движется с наибольшей скоростью. В мелких сосудах практически вся кровь оказывается вблизи сосудистой стенки, поэтому быстротекущего центрального потока крови просто не существует. Сложив скорости всех концентрических слоев текущей крови, умноженные на площади поперечного сечения каждого слоя, можно вывести формулу, известную как закон Пуазейля:
где F — скорость кровотока, АР — разница давления на концах сосуда, r — радиус сосуда, 1 — длина сосуда и n — вязкость крови. Обратите внимание, что в этом уравнении скорость кровотока прямо пропорциональна четвертой степени радиуса сосуда. Это еще раз показывает, что среди всех факторов, определяющих скорость кровотока, диаметр кровеносного сосуда, равный двум радиусам, имеет первостепенное значение. Влияние диаметра артериол на их сопротивление (закон четвертой степени). В большом круге кровообращения почти 2/3 общего периферического сопротивления приходится на мелкие артериолы. Внутренний диаметр артериол имеет величину от 4 до 25 мкм. Однако мощная мышечная стенка артериол позволяет существенно менять внутренний диаметр, часто более чем в 4 раза. Исходя из закона четвертой степени, который определяет зависимость объемного кровотока от диаметра сосудов, четырехкратное увеличение диаметра приводит к возрастанию объемного кровотока, по меньшей мере, в 256 раз. Таким образом, незначительные изменения диаметра артериол в ответ на нервные сигналы или действие местных гуморальных факторов может привести или к почти полному прекращению кровотока в тканях, или — в других экстремальных ситуациях — резко увеличить кровоток. И действительно, в отдельных сосудистых областях регистрируется увеличение местного кровотока в 100 раз при переходе артериол из состояния максимального сужения к состоянию их максимального расширения. Сопротивление сосудов, соединенных между собой последовательно и параллельно. Кровь, которая поступает в большой круг кровообращения из сердца, движется из области с высоким давлением (аорта) в область с низким давлением крови (полые вены). Кровь течет через обширную сосудистую сеть, в которой многочисленные сосуды соединены между собой последовательно и параллельно. Артерии, артериолы, капилляры, венулы и вены в целом являются системой последовательно соединенных сосудов. Общее сопротивление такой системы представляет собой сумму сопротивлений каждого отдельного сосуда:
Следовательно, общее периферическое сопротивление равно сумме сопротивлений артерий, артериол, капилляров, венул и вен. На примере, приведенном на рисунке, общее сосудистое сопротивление равно сумме сопротивлений R1 и R2. Благодаря разветвлению сосудов формируются параллельные сосудистые сети, снабжающие кровью многочисленные органы и ткани организма. Формирование параллельных сосудистых сетей позволяет каждому органу и даже участку органа в большой степени регулировать собственный местный кровоток независимо от других органов и тканей. Очевидно, что при одном и том же градиенте давления гораздо больший объем крови будет протекать через систему параллельных сосудов, чем через любой отдельно взятый сосуд. Таким образом, общее сопротивление системы параллельных сосудов оказывается гораздо меньше, чем сопротивление любого отдельного сосуда. Кровоток через каждый из параллельных сосудов на рисунке зависит от градиента давления и сопротивления данного сосуда, а не сопротивления всей системы. Однако увеличение сопротивления одного из сосудов параллельной системы приведет к увеличению сопротивления всей системы. Кажется парадоксальным, что дополнительное увеличение количества сосудов в параллельной системе приводит к уменьшению общего сосудистого сопротивления. Дело в том, что множество параллельных сосудов облегчает протекание крови через сосудистую сеть, т.к. каждый параллельный сосуд обеспечивает дополнительный путь кровотоку, увеличивая так называемую проводимость системы для крови. Итак, общая проводимость системы параллельных сосудов (Собщая) представляет собой сумму проводимостей каждого отдельного сосуда: Собщее = С1+С2+С3+С4…. Например, сосуды головного мозга, почек, мышц, желудочно-кишечного тракта, кожи, сердца представляют собой отдельные, параллельно соединенные системы, каждая из которых вносит свой вклад в общую проводимость большого круга кровообращения. Объемный кровоток каждого органа является частью общего кровотока (сердечного выброса) и зависит от сопротивления кровотоку (или проводимости) органа так же, как и от градиента давления. Следовательно, ампутация конечности или хирургическое удаление почки приводит к удалению одной из параллельных сосудистых систем большого круга кровообращения и уменьшает общую сосудистую проводимость и объемный кровоток (т.е. сердечный выброс), в то время как общее периферическое сопротивление увеличивается. – Вернуться в оглавление раздела “Физиология человека.” Оглавление темы “Сосудистая система”: |
Источник
Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:
Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.
Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.
Коэффициент гидравлического сопротивления
Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:
Δh= ΔP/(ρg)
где ρ — плотность среды, g — ускорение свободного падения.
В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
Поворотов
Диафрагм
Задвижек
Вентилей
Кранов
Различных ответвлений и тому подобного
На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.
Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.
hr = ξ υ2 / (2g)
где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).
Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.
Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.
В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.
Местные гидравлические сопротивления
Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.
Гидравлические потери на внезапное сужение трубы
Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.
ξвн. суж = 0,5(1- (F2/F1))
Значение коэффициента ξвн. суж от значения отношения (F2/F1)) можно найти в соответствующем справочнике по гидравлике.
Гидравлические потери при изменении направления трубопровода под некоторым углом
В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле
ξ поворот = 0,946sin(α/2) + 2.047sin(α/2)2
где α – угол поворота трубопровода.
Местные гидравлические сопротивления при входе в трубу
В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.
Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:
ξвх = 0,505 + 0,303sin α + 0,223 sin α2
Местные гидравлические сопротивления задвижки
На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.
Гидравлическое сопротивление полностью открытой запорной арматуры равно
ξвентиля = от 2,9 до 4,5
Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.
Гидравлические потери диафрагмы
Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:
режима движения жидкости
отношения диаметров отверстия диафрагмы и трубы
конструктивных особенностей диафрагмы.
Для диафрагмы с острыми краями:
ξдиафр = d02 / D02
Местные гидравлические сопротивления при входе струи под уровень жидкости
Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.
ξвхода = 1
Видео о гидравлическом сопротивлении
На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)
Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.
Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.
Вместе со статьей “Гидравлическое сопротивление” читают:
Источник