Формула объема цилиндрического сосуда
Ââåäèòå ðàäèóñ îñíîâàíèÿ è âûñîòó öèëèíäðà | |
| Ðàäèóñ: | |
| Âûñîòà: | |
Öèëèíäð – ãåîìåòðè÷åñêîå òåëî, êîòîðîå ïîëó÷àåòñÿ ïðè âðàùåíèè ïðÿìîóãîëüíèêà âîêðóã åãî ñòîðîíû. Òàêæå, öèëèíäð ïðåäñòàâëÿåò ñîáîé òåëî, îãðàíè÷åííîå öèëèíäðè÷åñêîé ïîâåðõíîñòüþ è äâóìÿ ïàðàëëåëüíûìè ïëîñêîñòÿìè, ïåðåñåêàþùèìè åå. Ýòà ïîâåðõíîñòü îáðàçóåòñÿ ïðè äâèæåíèè ïðÿìîé ïàðàëëåëüíî ñàìîé ñåáå. Ïðè ýòîì âûäåëåííàÿ òî÷êà ïðÿìîé ïåðåìåùàåòñÿ âäîëü îïðåäåëåííîé ïëîñêîé êðèâîé (íàïðàâëÿþùàÿ). Äàííàÿ ïðÿìàÿ íàçûâàåòñÿ îáðàçóþùåé öèëèíäðè÷åñêîé ïîâåðõíîñòè. Ôîðìóëà îáúåìà öèëèíäðà: , ãäå R – ðàäèóñ îñíîâàíèé, h – âûñîòà öèëèíäðà | |
|
| ||||||||||
|
| ||||||||||
|
| ||||||||||
Ìû â ñîöñåòÿõ Ïðèñîåäèíÿéòåñü! Íàøëè îøèáêó? Åñòü ïðåäëîæåíèÿ? Ñîîáùèòå íàì |
Ýòîò êàëüêóëÿòîð ìîæíî âñòàâèòü íà ñàéò, â áëîã Ñîçäàäèì êàëüêóëÿòîð äëÿ âàñ |
Источник
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Объем правильного цилиндра через радиус и высоту цилиндра
– Вычисления (показано) (скрыто)
– примечания (показано) (скрыто)
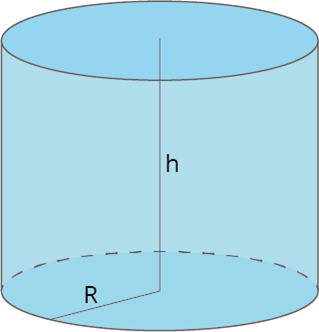
r – радиус основания цилиндра
h – высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

S – площадь основания цилиндра
h – высота цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

d – диаметр основания цилиндра
h – высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Объем цилиндрической полости
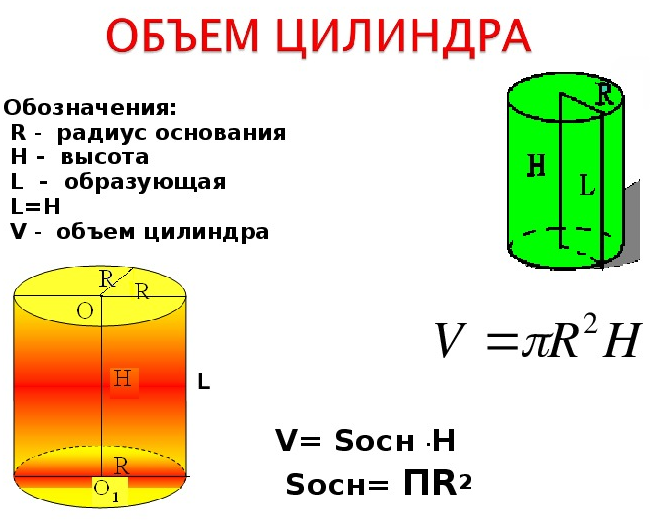
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
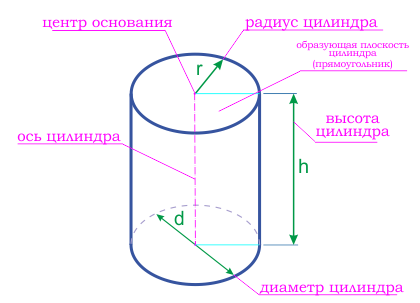
Цилиндр может быть правильным или наклонным .
.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Поверхности цилиндра
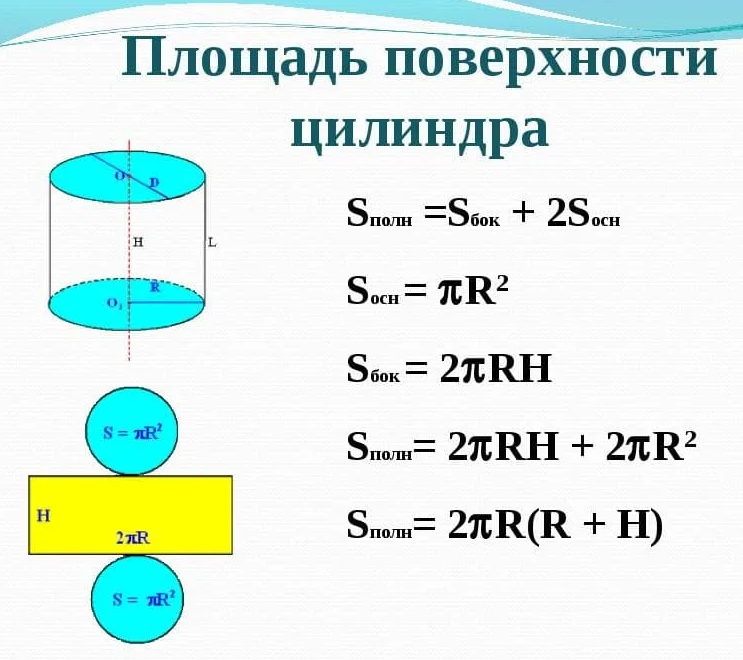
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
.
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса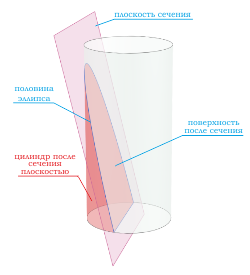 .
.
Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм3, см3, мл3.
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем полого цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки
Источник
Определение цилиндра
Цилиндр – геометрическое тело, получаемое при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор объема цилиндра
Это определение самого простого, так называемого, прямого кругового цилиндра. Более полное и общее определение цилиндра следующее:
Цилиндром называют геометрическое тело, которое получается путем пересечения двух плоскостей, которые параллельны друг другу, с прямыми, которые так же параллельны друг другу.
Эти прямые получили название образующих цилиндра. Плоскости – это основания цилиндра.
Прямая, которая перпендикулярна плоскостям, содержащим основания цилиндра, называется высотой данного цилиндра.
Типы цилиндров
Они зависят от того, под каким углом пересекаются основания и образующие цилиндра. Если угол равен 90 градусам, тогда цилиндр называется прямым. Линия, которая соединяет центр одного основания с другим, называется осью симметрии. Если угол не прямой, то цилиндр называется наклонным (косым).
Если форма основания цилиндра – гипербола, то цилиндр гиперболический, если парабола, круг или эллипс, то, соответственно параболический, круговой и эллиптический.
Формула объема кругового цилиндра
Для того, чтобы вычислить объем прямого кругового цилиндра нужно просто умножить площадь его основания (то есть, площадь круга, лежащего в основании цилиндра) на высоту этого цилиндра.
Формула объема кругового цилиндра
V = S осн ⋅ h V=S_{text{осн}}cdot h V=Sосн⋅h
S осн S_{text{осн}} Sосн – площадь основания цилиндра;
h h h – высота этого цилиндра.
Для кругового цилиндра, площадь основания S осн S_{text{осн}} Sосн это площадь круга:
S осн = π ⋅ R 2 S_{text{осн}}=picdot R^2 Sосн=π⋅R2
R R R – радиус круга.
Рассмотрим несколько примеров.
Задача 1
Найдите объем цилиндра, если площадь его основания равна 196 π см 2 196pitext{ см}^2 196π см2, а его высота h h h в 2 раза больше радиуса основания R R R.
Решение
S осн = 196 π S_{text{осн}}=196pi Sосн=196π
h = 2 ⋅ R h=2cdot R h=2⋅R
Сначала вычисляем радиус основания:
S осн = π ⋅ R 2 S_{text{осн}}=picdot R^2 Sосн=π⋅R2
Выразим отсюда радиус R R R:
R 2 = S осн π R^2=frac{S_{text{осн}}}{pi} R2=πSосн
R = S осн π R=sqrt{frac{S_{text{осн}}}{pi}} R=πSосн
R = 196 π π R=sqrt{frac{196pi}{pi}} R=π196π
R = 196 R=sqrt{196} R=196
R = 14 R=14 R=14
По условию задачи, высота цилиндра в два раза больше R R R:
h = 2 ⋅ R = 2 ⋅ 14 = 28 h=2cdot R=2cdot 14=28 h=2⋅R=2⋅14=28
Тогда объем цилиндра по формуле:
V = S осн ⋅ h = 196 ⋅ π ⋅ 28 ≈ 17232 см 3 V=S_{text{осн}}cdot h=196cdotpicdot28approx17232text{ см}^3 V=Sосн⋅h=196⋅π⋅28≈17232 см3
Ответ
17232 см 3 . 17232text{ см}^3. 17232 см3.
Задача 2
Определить, чему равен объем цилиндра, если радиус его основания R R R равен 7 см 7text{ см} 7 см, а высота – 14 см 14text{ см} 14 см.
Решение
R = 7 R=7 R=7
h = 14 h=14 h=14
По формуле для объема цилиндра получаем:
V = S осн ⋅ h = π ⋅ R 2 ⋅ h = π ⋅ 7 2 ⋅ 14 ≈ 2154 см 3 V=S_{text{осн}}cdot h=picdot R^2cdot h=picdot7^2cdot14approx2154text{ см}^3 V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3
Ответ
2154 см 3 . 2154text{ см}^3. 2154 см3.
Задача 3
В квадрат со стороной a a a равной 4 см 4text{ см} 4 см вписана окружность, являющаяся основанием цилиндра, высота которого равна 20 см 20text{ см} 20 см. Вычислите его объем.
Решение
a = 4 a=4 a=4
h = 20 h=20 h=20
Исходя из того, что сторона квадрата, в который вписана окружность, равна диаметру D D D этой окружности, можно найти площадь основания цилиндра:
S осн = π ⋅ R 2 = π ⋅ D 2 4 = π ⋅ a 2 4 = π ⋅ 4 2 4 ≈ 12.56 S_{text{осн}}=picdot R^2=frac{picdot D^2}{4}=frac{picdot a^2}{4}=frac{picdot 4^2}{4}approx12.56 Sосн=π⋅R2=4π⋅D2=4π⋅a2=4π⋅42≈12.56
Объем цилиндра:
V = S осн ⋅ h ≈ 12.56 ⋅ 20 = 251.2 см 3 V=S_{text{осн}}cdot happrox12.56cdot20=251.2text{ см}^3 V=Sосн⋅h≈12.56⋅20=251.2 см3
Ответ
251.2 см 3 . 251.2text{ см}^3. 251.2 см3.
Тест по теме «Объем цилиндра»
Источник
Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
V = π R2h
V = So h
где V – объем цилиндра,
So – площадь основания цилиндра,
R – радиус цилиндра,
h – высота цилиндра,
π = 3.141592.
Смотрите также онлайн калькулятор для расчета объема цилиндра
Объем цилиндра формула (через радиус основания и высоту)
{V=pi r^2 h}, где
r – радиус основания цилиндра,
h – высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что {pi r^2} – это формула площади круга, а в нашем случае – площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
Зная радиус r и высоту h
Чему равен объем цилиндра если его радиус
r = ,
а высота
h = ?
Ответ: V =
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r2⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра если его диаметр
d = ,
а высота
h = ?
Ответ: V =
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(d/2)2⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H

2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2)2 ⋅ H
Введите радиус основания и высоту цилиндра
Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см2 ⋅ 10 см = 785 см3.
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.
Поэтапный расчет объема картонной коробки
Для расчета нужно:
- Измерить длину а и ширину b, если дно коробки квадратное, то а=b;
- Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5-10 мм меньше, чем внутренние размеры гофроупаковки.
Формула для вычисления объема V в м3 коробки с прямоугольным или квадратным основанием:
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
Если в основании коробки не прямоугольник, а треугольник, пяти- или шестиугольник, то формула вычисления объема будет:
V=S*h
где S – площадь основания коробки, а h – ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки – в этой статье
| Радиус: | ||
| Высота: | ||
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула объема цилиндра: , где R – радиус оснований, h – высота цилиндра | ||
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м3 >;
зная равенство: 1 м3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
Цилиндр может быть правильным или наклонным

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
[ LARGE V = S cdot H ]
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник
 , но две боковые стороны которого будут являться кривыми линиями.
, но две боковые стороны которого будут являться кривыми линиями.Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса

Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Формула расчета объема цилиндра
Объем цилиндра вычисляется как произведение площади основания на высоту цилиндра. Так как основанием цилиндра является круг, площадь основания можно рассчитать через радиус или диаметр.
Найти объем цилиндра
 Выберите известные величины:
Выберите известные величины:Введите данные:
Вводить можно числа или дроби (-2.4, 5/7, …).
Источники
- https://ru.onlinemschool.com/math/formula/volume/
- https://mnogoformul.ru/obem-cilindra
- https://poschitat.online/obem-cilindra
- https://MicroExcel.ru/obyom-tsilindra/
- https://www.calc.ru/obyem-tsilindra.html
- https://gofro-karton.com/blog/rasschitat_obem_korobki/
- https://tara-tovara.ru/docs/poleznaya_rm/kak_rasschitat_obem_korobki_v_m3_i_litrakh/
- https://doza.pro/art/math/geometry/cylinder
- https://calcsbox.com/post/formula-obema-cilindra.html
- https://kalkulyator-nds.com/obem-cilindra-kalkulyator
- https://ru.onlinemschool.com/math/assistance/figures_volume/cylinder/
Источник
