Формула объема сосуда физика
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
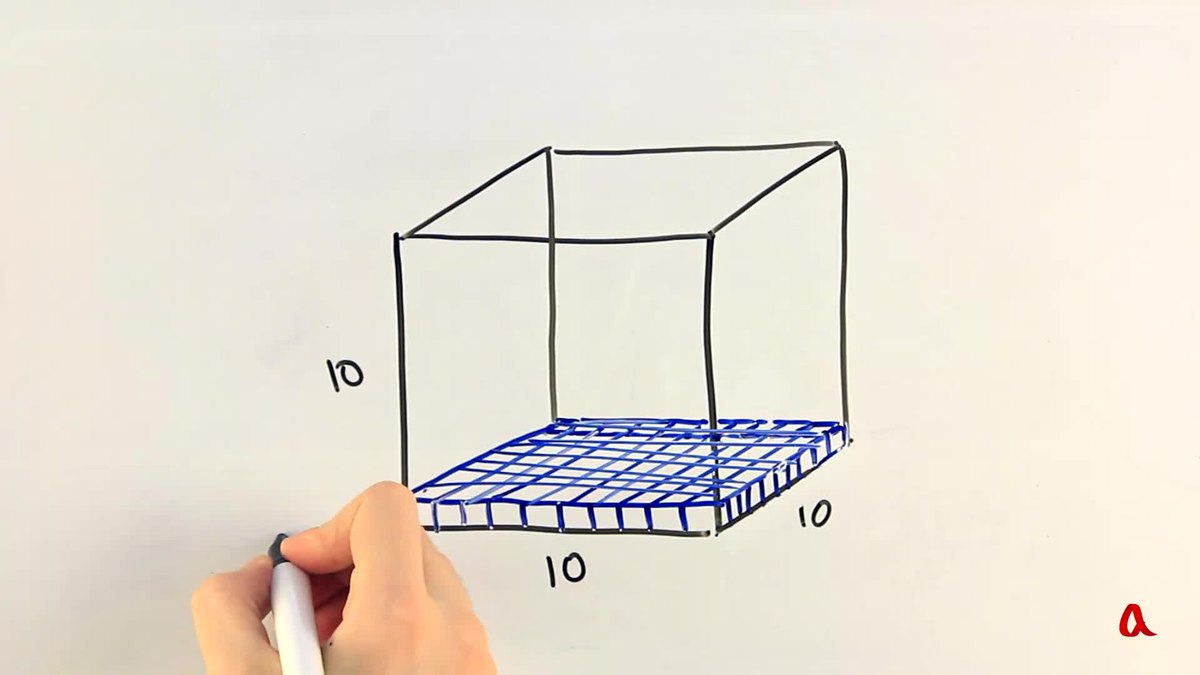
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 – интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 – интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 – интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 – интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 – интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
У этого термина существуют и другие значения, см. Объём (значения).
Объём – количественная характеристика пространства, занимаемого телом или веществом. С понятием объёма тесно связано понятие вместимости – объёма внутреннего пространства сосуда, упаковочного ящика и т. п. Объём тела (как и вместимость сосуда) определяется его формой и линейными размерами. Основное свойство объёма – аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей[1].
Единица объёма в СИ – кубический метр; от неё образуются производные единицы – кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма – галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume – «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма[править | править код]
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.
Математически[править | править код]
Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром вычисляется с помощью выражения , а объём прямоугольного параллелепипеда – умножением его длины на ширину и на высоту.
Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Сводка формул[править | править код]
Через плотность[править | править код]
Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: .
Единицы объёма жидкости[править | править код]
- 1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские[2][править | править код]
- Ведро = 12,3 литра
- Бочка = 40 вёдер = 492 литра
Английские[править | править код]
- 1 пинта = 0,568 литра
- 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
- 1 галлон = 8 пинтам = 4,55 литра
- 1 галлон (амер.) = 3,785 литра
Античные[править | править код]
- Котила = 0,275 литра
Древнееврейские[3][править | править код]
- Эйфа = 24,883 литра
- Гин = 1/6 эйфы = 4,147 литра
- Омер = 1/10 эйфы = 2,4883 литра
- Кав = 1/3 гина = 1,382 литра
Единицы объёма сыпучих веществ[править | править код]
Русские[править | править код]
- Четверик = 26,24 литра (1 пуд зерна)
- Гарнец = 3,28 литра
- Четверть = 1/4 ведра = 3,075 литра
- Штоф = 1/8 ведра = 1,54 литра
- Кружка = 1/10 ведра = 1,23 литра
- Бутылка (винная) = 1/16 ведра = 0,77 литра
- Бутылка (пивная) = 1/20 ведра = 0,61 литра
- Чарка = 1/10 кружки = 0,123 литра
- Шкалик (косушка) = 1/2 чарки = 0,0615 литра
Английские[править | править код]
- 1 бушель = 8 галлонов = 36,36872 литра
- 1 баррель = 163,65 литра
Прочие единицы[править | править код]
- 1 унция (англ.) = 2,841⋅10−5 м³
- 1 унция (амер.) = 2,957⋅10−5 м³
- 1 кубический дюйм = 1,63871⋅10−5 м³
- 1 кубический фут = 2,83168⋅10−2 м³
- 1 кубический ярд = 0,76455 м³
- 1 кубическая астрономическая единица =3,348⋅1024 км³
- 1 кубический световой год = 8,466⋅1038 км³
- 1 кубический парсек = 2,938⋅1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅1049 км³
Примечания[править | править код]
Литература[править | править код]
- Объём // Математическая энциклопедия (в 5 томах). – М.: Советская Энциклопедия, 1982. – Т. 3.
- Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). – СПб., 1890-1907.
Ссылки[править | править код]
- Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020.
Источник
2 октября 2011
Автор КакПросто!
Объем определяет величину пространства, которую занимает какое-либо тело. Эта величина связана постоянными соотношениями с другими характеристиками физических тел – их геометрическими размерами, весом и плотностью. Поэтому измерение этих дополнительных параметров может стать базой для вычисления объема, например, сосуда.
Инструкция
Если есть возможность наполнить сосуд водой, то для определения его объема достаточно иметь какую-либо мерную форму. В зависимости от размеров сосуда мерной посудой может стать шприц, мензурка, стакан, банка, ведро или любая другая посуда, вместимость которой вам известна. Подобрав подходящий измерительный сосуд, заполните водой до краев сосуд исследуемый, а затем переливайте воду в измерительный сосуд, отсчитывая таким образом объем.
Если заполнить исследуемый сосуд жидкостью нет возможности, но можно поместить его в жидкость, то определите объем по количеству вытесненной им воды. Для этого тоже потребуется какая-либо мерная посуда. Заполнив ее частично водой, отметьте уровень, затем поместите в мерную посуду исследуемый сосуд таким образом, чтобы он полностью оказался под водой, и сделайте вторую отметку. Затем определите разницу объемов мерной посуды по разнице двух сделанных отметок.
Если мерной посуды нет, но есть возможность взвешивать сосуд, то определите разницу между сосудом пустым и заполненным водой. Исходя из того, что один кубический метр объема должен вмещать воду, весом в одну тонну, рассчитайте объем сосуда.
Если сосуд имеет геометрически правильную форму, то его объем можно рассчитать, измерив размеры. Для нахождения объема сосуда цилиндрической формы (например, кастрюли) надо измерить диаметр (d) его основания (дна кастрюли) и ее высоту (h). Объем (V) будет равен одной четверти от произведения возведенного в квадрат диаметра на высоту и число Пи: V=d²∗h∗π/4.
Для нахождения объема сосуда, имеющего форму шара, достаточно определить его диаметр (d). Объем (V) будет равен одной шестой части от произведения возведенного в куб диаметра на число Пи: V=d³∗π/6. Если измерить длину окружности (L) шарообразного сосуда в самой широкой его части проще (например, с помощью сантиметра), чем измерить диаметр, то объем можно рассчитать и через эту величину. Возведенную в куб длину окружности надо разделить на увеличенное в шесть раз число Пи, возведенное в квадрат: V=L³/(π²∗6).
Для нахождения объема (V) сосуда прямоугольной формы, надо измерить его длину, ширину и высоту (a, b и h) и перемножить полученные значения: V=a∗b∗h. Если этот сосуд имеет кубическую форму, то достаточно возвести длину одного его ребра в третью степень: V=a³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Источник
Что такое вместимость сосуда
Вместимость сосуда – это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ – кубический метр, но в случае жидкости чаще используют литр.
Особенности расчета объема жидкости в сосуде
Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества – твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.
В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.
За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:
(h = frac{p}{rho s g}.)
(p) здесь – давление в паскалях, (rho) – плотность, (g) – ускорение свободного падения, константа.
Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.
При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов.
Задача
Найти объем керосина, зная массу одного и того же сосуда с ним, и без него. Масса пустого сосуда 440 грамм, полного – 600 грамм.
Решение:
Плотность керосина можно узнать из справочной таблицы – 800 (frac{кг}{м^{3}}.)
Вычислим массу керосина в сосуде: 600 – 440 = 160.
Подставим известные данные в формулу:
(V = frac{m}{rho} = frac{0,16}{800} = 0,0002 м^{3} = 200 см^{3}.)
Ответ: 200 (см^{3}.)
Как определить вместимость сосудов разных форм
Вычисление объема параллелепипеда
Параллелепипед – это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.
(V = S_{осн} s H. )
Прямоугольный параллелепипед – это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, – это куб.
Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
(V = AB s AD s AA_{1} = abc.)
Объем куба равен кубу его стороны:
(V = a^{3}.)
Нахождение объема пирамиды
Пирамида – это многогранник, состоящий из основания – плоского многоугольника, вершины – точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды – это перпендикуляр, опущенный из вершины на плоскость основания.
(V = frac{1}{3} s S_{осн} s h.)
Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований – (S_{1}) и (S_{2}).
(V = frac{1}{3} s h s (S_{1} + S_{2} + sqrt{S_{1} s S_{2}}). )
Как найти объем цилиндра
Цилиндр – это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
(R) – радиус основания цилиндра, (h) – его высота, равная образующей оси.
(V = S_{осн} s h = pi s R^{2} s h.)
Если нужно найти объем усеченного цилиндра, то понадобится не только R – радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l – (l_{1}) и (l_{2}).
(V = pi s R^{2} s frac{l_{1} + l_{2}}{2}.)
Как высчитать объем конуса
Конус – это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.
(V = frac{1}{3} s S_{осн} s h = frac{1}{3} s pi s R^{2} s h.)
Чтобы найти объем усеченного конуса, понадобятся (R_{1}) и (R_{2}) – радиусы оснований, а также высота (h).
(V = frac{pi s h}{3} s (R_1^2 + R_2^2 + R_1 s R_2).)
Нахождение объема шара
Шар – это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.
(R) – радиус полукруга, равный радиусу шара.
(V = frac{4pi s R^{3}}{3}.)
Источник
| Объем | |
|---|---|
Мерный стаканчик можно использовать для измерения объемов жидкостей . Эта чашка измеряет объем в стаканах , жидких унциях и миллилитрах . | |
Общие символы | V |
| Единица СИ | Кубический метр [м 3 ] |
Прочие единицы | Литр , жидкая унция , галлон , кварта , пинты , чайная ложка , драма жидкости , в 3 , ярде 3 , бочка |
| В базовых единицах СИ | 1 м 3 |
| Измерение | L 3 |
Объем представляет собой количество из трехмерного пространства заключенного в замкнутой поверхности , например, пространство , что вещество ( твердая , жидкая , газ , или плазма ) или 3D – форма занимает или содержит. Объем часто определяется численно с использованием производной единицы СИ – кубического метра . Под объемом контейнера обычно понимают вместимость контейнера; т.е. количество жидкости (газа или жидкости), которое может вместить контейнер, а не количество пространства, которое сам контейнер вытесняет. Трехмерным математическим формам также приписываются объемы. Объемы некоторых простых форм, таких как правильные, прямые и круглые, можно легко вычислить с помощью арифметических формул . Объемы сложных форм можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Одномерные фигуры (например, линии ) и двухмерные фигуры (например, квадраты ) получают нулевой объем в трехмерном пространстве.
Объем твердого тела (правильной или неправильной формы) можно определить по вытеснению жидкости . Вытеснение жидкости также можно использовать для определения объема газа. Совокупный объем двух веществ обычно больше, чем объем только одного из веществ. Тем не менее, иногда один растворяет вещество в другой и в таких случаях комбинированного объема не является аддитивным .
В дифференциальной геометрии объем выражается через форму объема и является важным глобальным римановым инвариантом . В термодинамике объем является фундаментальным параметром и является переменной, сопряженной с давлением .
Единицы измерения
Любая единица длины дает соответствующую единицу объема: объем куба , стороны которого имеют заданную длину. Например, кубический сантиметр (см 3 ) – это объем куба, длина сторон которого составляет один сантиметр (1 см).
В Международной системе единиц (СИ) стандартной единицей объема является кубический метр (м 3 ). Метрическая система также включает в себя литр (L) в качестве единицы объема, где один литр объем 10-сантиметрового куб. Таким образом
1 литр = (10 см) 3 = 1000 кубических сантиметров = 0,001 кубических метров,
так
1 кубический метр = 1000 литров.
Небольшие количества жидкости часто измеряются в миллилитрах , где
1 миллилитр = 0,001 литра = 1 кубический сантиметр.
Таким же образом можно измерить большие количества в мегалитрах, где
1 миллион литров = 1000 кубометров = 1 мегалитр.
Также используются различные другие традиционные единицы объема, включая кубический дюйм , кубический фут , кубический ярд , кубическую милю , чайную ложку , столовую ложку , жидкую унцию , жидкий драм , жабры , пинту , кварту. , то галлон , то минит , то ствол , то шнур , то клюнет , то бушель , то хогсхед , то акр-фут и доска для ног .
В Оксфордском словаре английского языка вместимость определяется как «мера, применяемая к содержимому сосуда, а также к жидкостям, зерну и т.п., которые принимают форму того, что их удерживает». (Слово « емкость» имеет другие значения, не связанные, например, с управлением мощностью .) «Емкость» не тождественна по значению объему, хотя и тесно связана; вместимость контейнера всегда равна его внутреннему объему. Единицы измерения емкости – это литр СИ и его производные единицы, а также британские единицы, такие как жабры , пинта , галлон и другие. Единицы объема – это кубы единиц длины . В системе СИ единицы объема и вместимости тесно связаны: один литр равен 1 кубическому дециметру, вместимость куба со стороной 10 см. В других системах преобразование нетривиально; Емкость топливного бака транспортного средства редко указывается в кубических футах, например, в галлонах (британский галлон заполняет объем 0,1605 куб. фута).
Плотность объекта определяется как отношение массы к объему. Плотность, обратная величине, – это удельный объем, который определяется как объем, деленный на массу. Удельный объем – это понятие, важное в термодинамике, где объем рабочего тела часто является важным параметром изучаемой системы.
Объемная скорость потока в динамике жидкости представляет собой объем жидкости , который проходит через заданную поверхность за единицу времени (например , кубических метров в секунду [м 3 с -1 ]).
Объем в исчислении
В исчислении , разделе математики , объем области D в R 3 задается тройным интегралом постоянной функции по области и обычно записывается как:
В цилиндрических координатах объемный интеграл равен
В сферических координатах (используя условные обозначения для углов в качестве азимута и отсчитываемых от полярной оси; см. Дополнительные условные обозначения ), интеграл объема равен
Формулы объема
Соотношение объемов конуса, сферы и цилиндра одинакового радиуса и высоты
Конус, сфера и цилиндр радиуса r и высоты h
Приведенные выше формулы можно использовать, чтобы показать, что объемы конуса , сферы и цилиндра одинакового радиуса и высоты находятся в соотношении 1: 2: 3 , как показано ниже.
Пусть радиус равен r, а высота равна h (что составляет 2 r для сферы), тогда объем конуса равен
объем шара
а объем цилиндра
Архимеду приписывают открытие отношения 2: 3 объемов сферы и цилиндра .
Вывод формулы объема
Сфера
Объем сферы – это интеграл бесконечного числа бесконечно малых круглых дисков толщиной dx . Расчет объема сферы с центром 0 и радиусом r выполняется следующим образом.
Площадь круглого диска составляет .
Радиус круглых дисков, определяемый таким образом, чтобы ось x пересекала их перпендикулярно, составляет
или же
где y или z могут быть взяты для представления радиуса диска при определенном значении x.
Используя y как радиус диска, объем сферы можно рассчитать как
Сейчас
Объединение урожайности
Эту формулу можно получить быстрее, используя формулу для площади поверхности сферы , которая равна . Объем сферы состоит из слоев бесконечно тонких сферических оболочек, а объем сферы равен
Конус
Конус представляет собой разновидность пирамидальной формы. Фундаментальное уравнение для пирамид, в три раза превышающее высоту основания, умноженную на высоту, применимо и к конусам.
Однако, используя математический анализ, объем конуса представляет собой интеграл бесконечного числа бесконечно тонких круглых дисков толщиной dx . Расчет объема конуса высотой h с центром в точке (0, 0, 0) с радиусом r выполняется следующим образом.
Радиус каждого кругового диска равен r, если x = 0, и 0, если x = h , и линейно изменяется между ними, то есть
Тогда площадь поверхности круглого диска равна
Тогда объем конуса можно рассчитать как
и после извлечения констант
Интеграция дает нам
Многогранник
Объем в дифференциальной геометрии
В дифференциальной геометрии , разделе математики , форма объема на дифференцируемом многообразии – это дифференциальная форма высшей степени (т. Е. Степень которой равна размерности многообразия), которая нигде не равна нулю. Многообразие имеет форму объема тогда и только тогда, когда оно ориентируемо. Ориентируемое многообразие имеет бесконечно много форм объема, поскольку умножение формы объема на функцию, отличную от нуля, дает другую форму объема. На неориентируемых многообразиях вместо этого можно определить более слабое понятие плотности . Интегрирование формы объема дает объем коллектора в соответствии с этой формой.
Ориентированное псевдориманово многообразие имеет естественную форму объема. В местных координатах это можно выразить как
где are 1-формы, которые образуют положительно ориентированный базис кокасательного расслоения многообразия, и является определителем матричного представления метрического тензора на многообразии в терминах того же базиса.
Объем в термодинамике
В термодинамике , то объем из системы является важным обширен параметром для описания его термодинамического состояния . Объемное удельное , интенсивное свойство , является громкость системы на единицу массы. Объем является функцией состояния и зависит от других термодинамических свойств, таких как давление и температура . Например, объем связан с давлением и температурой в качестве идеального газа по идеальному газу .
Расчет объема
Задача численного вычисления объема объектов изучается в области вычислительной геометрии в информатике, исследуются эффективные алгоритмы для выполнения этого вычисления, приблизительно или точно , для различных типов объектов. Например, метод аппроксимации выпуклого объема показывает, как аппроксимировать объем любого выпуклого тела с помощью оракула членства .
Смотрите также
Рекомендации
Внешние ссылки
| Викискладе есть медиафайлы по теме томов . |
Источник
