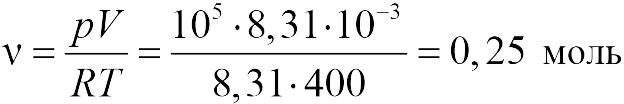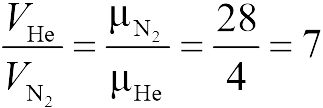Формула объема сосуда газа

19 ноября 2011
Автор
КакПросто!
Газ, как и вещества, находящиеся в других агрегатных состояниях, имеет ряд параметров, в число которых входит и объем. Объем газа находится на основании других его характеристик, которые приведены в условии задачи. Любой газ, независимо от вида и состава, имеет объем, который и требуется найти во многих задачах.
Инструкция
Газ, независимо от его состава, имеет три основных параметра: массу, объем и плотность. В большинстве задач оперируют так называемым идеальным газом, поэтому опираться в них необходимо лишь на приведенные в условии значения массы, давления, температуры. Например, в условии задачи может быть указан газ азот N2 с температурой в 60 градусов, давлением в 30 кПа и массой в 0,05 г. Зная эти три параметра и состав газа, по уравнению Менделеева-Клапейрона можно найти его объем. Для этого необходимо переделать данное уравнение следующим образом:
pV=mRT/M.
Осуществив дальнейшее преобразование формулы, найдите объем азота:
V =mRT/pM.
При этом молярную массу M можно найти по таблице Д.И. Менделеева. У азота она равна 12 г/моль. Тогда:
V=0,05*12*8,31*333/30*12≈4,61.
Если известны объем при нормальных условиях, а объем при других условиях является искомым, примените законы Бойля-Мариотта и Гей-Люссака:
pV/T=pнVн/Tн.
В таком случае преобразуйте формулу следующим образом:
pV*Tн=pнVн*T.
Отсюда объем V равен:
V=pнVн*T/p*Tн.
Индекс н означает величину того или иного параметра при нормальных условиях.
Если рассматривать объем газа с точки зрения термодинамики, можно заметить, что на газы могут действовать силы, за счет которых меняется объем. При этом давление газа постоянно, что характерно для изобарных процессов. В ходе таких процессов объем изменяется с одной величины на другую. Их можно обозначить как V1 и V2. В условиях ряда задач описывается некоторый газ, находящийся под поршнем в сосуде. При расширении этого газа поршень передвигается на некоторое расстояние dl, в результате чего осуществляется работа:
A=pdV=p(V2 -V1).
Эта формула связывает изменение объема газа и работу. Как известно, если дан конечный объем V2, то можно найти начальный объем V1:
V1=pV2-A/p.
Наконец, наиболее просто найти объем газа, исходя из двух других физических параметров – массы и плотности. Если в условиях задан газ с некоторой плотностью и массой, то его объем следует вычислять по формуле:
V=m/ρ.
У каждого газа имеется определенная плотность, как и у любого твердого или жидкого вещества. Поэтому, находя объем газа, в первую очередь необходимо учитывать именно этот параметр.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Источник
2 сентября 2011
Автор
КакПросто!
Объем газа можно найти с помощью нескольких формул. Выбрать подходящую нужно, исходя из данных в условии задачи величин. Большую роль при подборе необходимой формулы играют условия среды, а в частности: давления и температура.
Инструкция
Наиболее часто встречающаяся в задачах формула: V = n*Vm, где V – объем газа (л), n – количество вещества (моль), Vm – молярный объем газа (л/моль), при нормальных условиях(н.у.) является стандартной величиной и равен 22,4 л/моль. Бывает так, что в условии нет количества вещества, но есть масса определенного вещества, тогда поступаем так: n = m/M, где m – масса вещества (г), M – молярная масса вещества (г/моль). Молярную массу находим по таблице Д.И. Менделеева: под каждым элементом написана его атомная масса, складываем все массы и получаем необходимую нам. Но такие задачи встречаются довольно редко, обычно в задачи присутствует уравнение реакции. Решение таких задач по этом немного изменяется. Рассмотрим на примере.
Какой объем водорода выделится при нормальных условиях, если растворить алюминий массой 10,8 г в избытке соляной кислоты.
Записываем уравнение реакции: 2Al + 6HCl(изб.) = 2AlCl3 + 3H2.
Решаем задачу о этому уравнению. Находим количество вещества алюминия, которое вступило в реакцию: n(Al) = m(Al)/M(Al). Чтобы подставить данные в эту формулу, нам необходимо подсчитать молярную массу алюминия: M(Al) = 27 г/моль. Подставляем: n(Al) = 10,8/27 = 0,4 моль.Из уравнения мы видим, что при растворении 2 моль алюминия образуется 3 моль водорода. Рассчитываем какое же количество вещества водорода образуется из 0,4 моль алюминия: n(H2) = 3*0,4/2 = 0,6 моль. Затем подставляем данные в формулу по нахождению объема водорода: V = n*Vm = 0,6*22,4 = 13,44 л. Вот мы и получили ответ.
Если мы имеем дело с газовой системой, то имеет место такая формула: q(x) = V(x)/V, где q(x)(фи) – объемная доля компонента, V(x) – объем компонента (л), V – объем системы (л). Для нахождения объема компонента получаем формулу: V(x) = q(x)*V. А если необходимо найти объем системы, то: V = V(x)/q(x).
Обратите внимание
Существуют и другие формулы для нахождения объема, но если необходимо найти объем газа подойдут только формулы, приведенные в этой статье.
Источники:
- “Пособие по химии”, Г.П. Хомченко, 2005.
- как найти объем работ
- Найти объем водорода при электролизе раствора ZnSO4
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Источник
27 декабря 2018
Автор
КакПросто!
Для расчета объема газа, который находится в некотором сосуде или помещении, найдите их объем геометрическими методами. Это связано с тем, что газ всегда занимает весь предоставленный ему объем. В том случае, если известно количество вещества или масса газа в нормальных условиях, найдите объем газа, умножив количество вещества на 0,0224 м³. Если же газ не находится в идеальных условиях, используйте специальные уравнения.
Вам понадобится
- рулетка или дальномер, термометр, манометр, таблица Менделеева.
Инструкция
Расчет объема газа геометрическими методамиЕсли сосуд заполнен газом, найдите его объем. Например, если комната имеет форму параллелепипеда, с помощью рулетки или дальномера определите ее длину, ширину и высоту в метрах. Полученные результаты перемножьте и получите объем газа в комнате, выраженный в м³. Если сосуд цилиндрический, измерьте его диаметр, возведите его в квадрат, умножьте на 3,14 и высоту цилиндра, которую тоже измерьте, получившееся число поделите на 4.
Расчет объема известной массы определенного газа в нормальных условияхЕсли газ находится в нормальных условиях (0ºС, 760 мм.ст.ст.), известна его масса и химическая формула, с помощью таблицы Менделеева определите его молярную массу, учитывая тот факт, что у большинства простых газов молекулы двухатомные. Затем массу газа поделите на его молярную массу, а полученное число умножьте на 0,0224. Получите объем газа в м³. Есть и другой способ. Если известна масса и вид газа, по специальной таблице найдите его плотность и поделите массу газа на его плотность. Получите объем газа. Если масса газа дана в килограммах, плотность берите в килограммах на метр кубический, если в граммах – в граммах на сантиметр кубический. Соответственно получится объем или в метрах, или в сантиметрах кубических.
Расчет массы газа через уравненияЕсли известная масса газа находится в реальных условиях, найдите количество его вещества, для чего массу поделите на молярную массу. Манометром измерьте давление газа, а термометром его температуру. Давление выразите в Паскалях, а температуру в Кельвинах. Отношение температуры к давлению умножьте на количество вещества газа, и число 8,31 результатом будет объем данного газа в м³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Источник
Воздух (или инертный газ), находящийся в запечатанном пакете с печеньем, расширяется, когда продукт поднят на значительную высоту над уровнем моря (ок. 2000 м)
Зако́н Бо́йля — Марио́тта — один из основных газовых законов, экспериментально установленный в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году[1]. Описывает поведение газа в изотермическом процессе. С точки зрения современной физики закон представляет собой следствие уравнения Клапейрона — Менделеева[2].
Формулировки[править | править код]
Утверждение закона Бойля — Мариотта состоит в следующем[3][4][5]:
При постоянных температуре и массе газа произведение давления газа на его объём постоянно.
В математической форме это утверждение записывается в виде формулы
где — давление газа; — объём газа, а — постоянная в оговоренных условиях величина. В общем случае значение определяется химической природой, массой и температурой газа.
Очевидно, что если индексом 1 обозначить величины, относящиеся к начальному состоянию газа, а индексом 2 — к конечному, то приведённую формулу можно записать в виде
.
Из сказанного и приведённых формул следует вид зависимости давления газа от его объёма в изотермическом процессе:
Эта зависимость представляет собой другое, эквивалентное первому, выражение содержания закона Бойля — Мариотта[4][5]
. Она означает, что
Давление некоторой массы газа, находящегося при постоянной температуре, обратно пропорционально его объёму.
Тогда связь начального и конечного состояний газа, участвовавшего в изотермическом процессе, можно выразить в виде:
Следует отметить, что применимость этой и приведённой выше формулы, связывающей начальные и конечные давления и объёмы газа друг с другом, не ограничивается случаем изотермических процессов. Формулы остаются справедливыми и в тех случаях, когда в ходе процесса температура изменяется, но в результате процесса конечная температура оказывается равной начальной.
Важно уточнить, что данный закон справедлив только в тех случаях, когда рассматриваемый газ можно считать идеальным. В частности, с высокой точностью закон Бойля — Мариотта выполняется применительно к разреженным газам. Если же газ сильно сжат, то наблюдаются существенные отступления от этого закона.
Закон Бойля — Мариотта, закон Шарля и закон Гей-Люссака, дополненные законом Авогадро, являются достаточной основой для получения уравнения состояния идеального газа.
Следствия[править | править код]
Закон Бойля — Мариотта утверждает, что давление газа в изотермическом процессе обратно пропорционально занимаемому газом объёму. Если учесть, что плотность газа[6] также обратно пропорциональна занимаемому им объёму, то мы придём к заключению:
При изотермическом процессе давление газа изменяется прямо пропорционально его плотности.
Известно, что сжимаемость, то есть способность газа изменять свой объём под действием давления, характеризуется коэффициентом сжимаемости[7]. В случае изотермического процесса говорят об изотермическом коэффициенте сжимаемости, который определяется формулой
где индекс T означает, что частная производная берётся при постоянной температуре. Подставляя в эту формулу выражение для связи давления и объёма из закона Бойля — Мариотта, получаем[5]:
Таким образом, приходим к выводу:
Изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления.
См. также[править | править код]
- Закон Гей-Люссака
- Закон Шарля
- Закон Авогадро
- Идеальный газ
- Уравнение состояния идеального газа
Примечания[править | править код]
Литература[править | править код]
- Петрушевский Ф. Ф. Бойля-Мариотта закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Источник
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
(13.1) |
где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
(13.2) |
Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
(13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где — постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где ![]() — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
— число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. 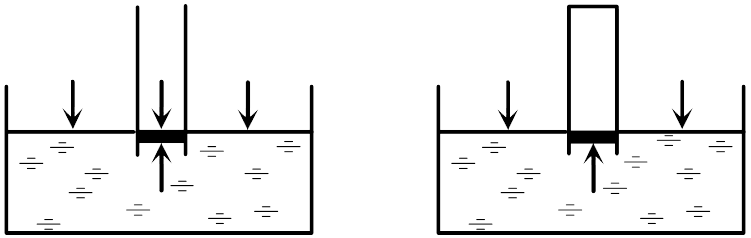 Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
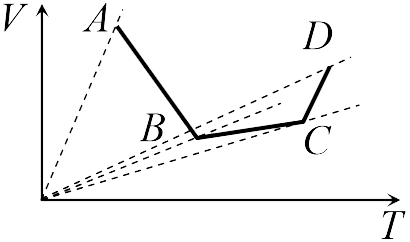
 Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
 Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
Если бы точки, отвечающие состояниям 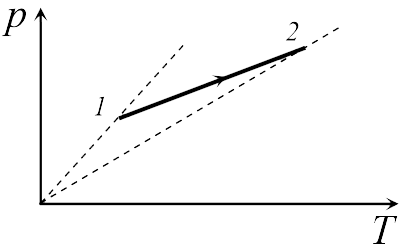 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь — масса газа, — масса одной молекулы газа.
Источник