Формула площади цилиндрическом сосуде
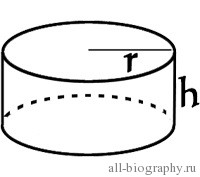
Цилиндр — геометрическое тело, которое можно получить при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор
На самом деле, это определение только самого простого, кругового цилиндра. Более общее определение цилиндрического тела следующее:
Цилиндром называют тело, образованное пересечением параллельных друг другу прямых и двух плоских поверхностей.
Такие прямые называются образующими данного цилиндра.
Прямая, перпендикулярная обоим основаниям, является высотой цилиндра.
Плоские поверхности называют основаниями данного цилиндра. Часто, они параллельны друг другу, но не всегда.
Виды цилиндра
Виды цилиндра зависят от того, под каким углом пересекаются образующие и основания нашего тела.
Если угол равен 90 градусам, то получим, так называемый, прямой цилиндр. У него есть ось симметрии – это перпендикуляр, соединяющий центры его оснований.
Если угол другой, то цилиндр называется наклонным.
Если форма основания – гипербола, то цилиндр гиперболический, если парабола — параболический, если эллипс — эллиптический, если круг — круговой.
Если основания цилиндра не параллельны, то он называется косым.
Формула площади поверхности цилиндра
Полная площадь поверхности цилиндра является суммой его боковой площади поверхности и площади оснований.
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}S=Sосн+Sбок
SоснS_{text{осн}}Sосн — площадь оснований;
SбокS_{text{бок}}Sбок — площадь боковой поверхности.
При вычислении площади поверхности цилиндра важным фактором является вид цилиндра. От него зависит и конкретная формула для площади.
Формула площади поверхности кругового цилиндра
Sосн=2⋅π⋅r2S_{text{осн}}=2cdotpicdot r^2Sосн=2⋅π⋅r2
Sбок=2⋅π⋅r⋅hS_{text{бок}}=2cdotpicdot rcdot hSбок=2⋅π⋅r⋅h
rrr — радиус круга (основания кругового цилиндра);
hhh — высота этого цилиндра.
Сокращенно, это формулу можно записать так:
S=Sосн+Sбок=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+2cdotpicdot rcdot h=2cdotpicdot rcdot(r+h)S=Sосн+Sбок=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)
Пример
Радиус круга, лежащего в основании прямого кругового цилиндра, имеет длину 6 (см.). Высота цилиндра – 20 (см.). Найдите полную площадь его поверхности.
Решение:
r=6r=6r=6
h=20h=20h=20
По формуле:
S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68S=2cdotpicdot rcdot(r+h)=2cdotpicdot 6cdot(6+20)approx979,68S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68 (см. кв.)
Ответ: 979,68 см. кв.
Формула площади поверхности наклонного кругового цилиндра
Sосн=2⋅π⋅r2S_{text{осн}}=2cdotpicdot r^2Sосн=2⋅π⋅r2
Sбок=p⋅lS_{text{бок}}=pcdot lSбок=p⋅l
rrr — радиус круга (основания кругового цилиндра);
ppp — периметр сечения наклонного цилиндра перпендикулярно образующей;
lll — длина образующей этого цилиндра.
Пример
Найти площадь поверхности наклонного цилиндра, если периметр ppp сечения плоскости, составляющей прямой угол с образующей, равен 30 (см.), а сама образующая равна 7 (см.) Радиус окружности, лежащей в основе цилиндра в два раза меньше его образующей.
Решение:
r=l2r=frac{l}{2}r=2l
p=30p=30p=30
l=7l=7l=7
Найдем сначала радиус основания:
r=l2=72=3.5r=frac{l}{2}=frac{7}{2}=3.5r=2l=27=3.5
Тогда полная площадь:
S=Sосн+Sбок=2⋅π⋅r2+p⋅l=2⋅π⋅3.52+30⋅7≈76,93+210=286,93S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+pcdot l=2cdotpicdot 3.5^2+30cdot 7approx76,93+210=286,93S=Sосн+Sбок=2⋅π⋅r2+p⋅l=2⋅π⋅3.52+30⋅7≈76,93+210=286,93 (см. кв.)
Ответ: 286,93 см. кв.
Тест по теме «Площадь поверхности цилиндра»
Источник
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr2 + πr2 = 2πr2.
Боковая поверхность цилиндра
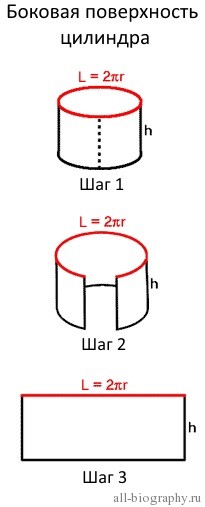Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
Sбок. = 2πrh
r – радиус цилиндра, h – высота цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: Sбок. = 2πrh
Sбок. = 2 * 3,14 * 2 * 3
Sбок. = 6,28 * 6
Sбок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr2 + 2πrh
S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
S = 376,8
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:
h = Sбок./2πr
Значение радиуса получаем из формулы: d = 2r
h = 24π / (2π * 0,5d)
h = 24π / (2π * 0,5 * 3)
h = 12 / 1,5
h = 8
Высота цилиндра равна 8.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Dark Spyro
5/5
Татьяна Матвиенко
5/5
Юрий Евдокимов
5/5
Михаил Чепурной
5/5
Дмитрий Новиков
5/5
Дилноза Саипова
4/5
Darya Simonova
5/5
Тамара Иванова
5/5
Татьяна Немчинова
5/5
Рамиль Сагиров
5/5
Оценка статьи
Средняя оценка: 4.6. Всего получено оценок: 9250.
Источник
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
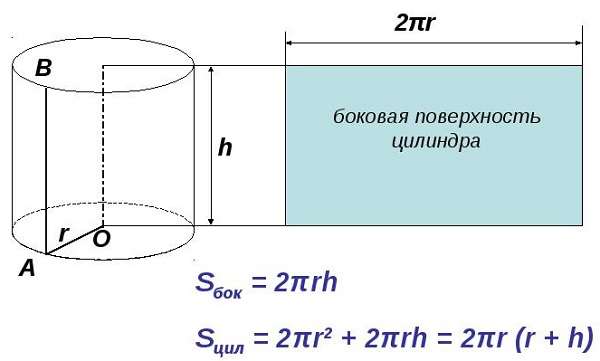
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.
Sбок = 2π * r * h,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.
Конечная формула выглядит следующим образом:
Sпол = 2π * r2 + 2π * r * h.
Площадь цилиндра формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
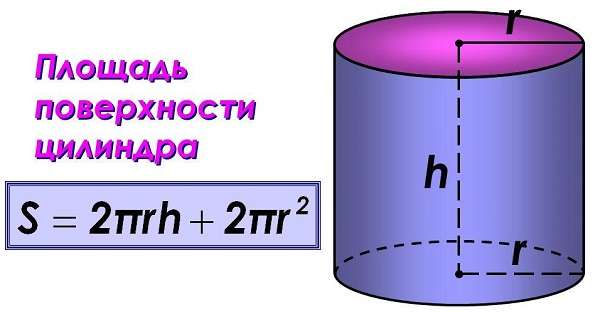
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,
Вместо r в полную формулу нужно вставить значение r = d/2.
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
Sпол = 2 * 3.14 * 242 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм2).
Переводим в привычные м2 и получаем 0,01868928, приблизительно 0.02 м2.
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м, высота 2 м. Используем формулу через диаметр:
Sпол = 3.14 * 0.22/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м2.
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
Sбок = 2 * 3.14 * 1 * 1 = 6.28 м2.
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Источник
Цилиндр — геометрическое тело, получаемое при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор объема цилиндра
Это определение самого простого, так называемого, прямого кругового цилиндра. Более полное и общее определение цилиндра следующее:
Цилиндром называют геометрическое тело, которое получается путем пересечения двух плоскостей, которые параллельны друг другу, с прямыми, которые так же параллельны друг другу.
Эти прямые получили название образующих цилиндра. Плоскости – это основания цилиндра.
Прямая, которая перпендикулярна плоскостям, содержащим основания цилиндра, называется высотой данного цилиндра.
Типы цилиндров
Они зависят от того, под каким углом пересекаются основания и образующие цилиндра. Если угол равен 90 градусам, тогда цилиндр называется прямым. Линия, которая соединяет центр одного основания с другим, называется осью симметрии. Если угол не прямой, то цилиндр называется наклонным (косым).
Если форма основания цилиндра — гипербола, то цилиндр гиперболический, если парабола, круг или эллипс, то, соответственно параболический, круговой и эллиптический.
Формула объема кругового цилиндра
Для того, чтобы вычислить объем прямого кругового цилиндра нужно просто умножить площадь его основания (то есть, площадь круга, лежащего в основании цилиндра) на высоту этого цилиндра.
Формула объема кругового цилиндра
V=Sосн⋅hV=S_{text{осн}}cdot hV=Sосн⋅h
SоснS_{text{осн}}Sосн — площадь основания цилиндра;
hhh — высота этого цилиндра.
Для кругового цилиндра, площадь основания SоснS_{text{осн}}Sосн это площадь круга:
Sосн=π⋅R2S_{text{осн}}=picdot R^2Sосн=π⋅R2
RRR — радиус круга.
Рассмотрим несколько примеров.
Задача 1
Найдите объем цилиндра, если площадь его основания равна 196π см2196pitext{ см}^2196π см2, а его высота hhh в 2 раза больше радиуса основания RRR.
Решение
Sосн=196πS_{text{осн}}=196piSосн=196π
h=2⋅Rh=2cdot Rh=2⋅R
Сначала вычисляем радиус основания:
Sосн=π⋅R2S_{text{осн}}=picdot R^2Sосн=π⋅R2
Выразим отсюда радиус RRR:
R2=SоснπR^2=frac{S_{text{осн}}}{pi}R2=πSосн
R=SоснπR=sqrt{frac{S_{text{осн}}}{pi}}R=πSосн
R=196ππR=sqrt{frac{196pi}{pi}}R=π196π
R=196R=sqrt{196}R=196
R=14R=14R=14
По условию задачи, высота цилиндра в два раза больше RRR:
h=2⋅R=2⋅14=28h=2cdot R=2cdot 14=28h=2⋅R=2⋅14=28
Тогда объем цилиндра по формуле:
V=Sосн⋅h=196⋅π⋅28≈17232 см3V=S_{text{осн}}cdot h=196cdotpicdot28approx17232text{ см}^3V=Sосн⋅h=196⋅π⋅28≈17232 см3
Ответ
17232 см3.17232text{ см}^3.17232 см3.
Задача 2
Определить, чему равен объем цилиндра, если радиус его основания RRR равен 7 см7text{ см}7 см, а высота – 14 см14text{ см}14 см.
Решение
R=7R=7R=7
h=14h=14h=14
По формуле для объема цилиндра получаем:
V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3V=S_{text{осн}}cdot h=picdot R^2cdot h=picdot7^2cdot14approx2154text{ см}^3V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3
Ответ
2154 см3.2154text{ см}^3.2154 см3.
Задача 3
В квадрат со стороной aaa равной 4 см4text{ см}4 см вписана окружность, являющаяся основанием цилиндра, высота которого равна 20 см20text{ см}20 см. Вычислите его объем.
Решение
a=4a=4a=4
h=20h=20h=20
Исходя из того, что сторона квадрата, в который вписана окружность, равна диаметру DDD этой окружности, можно найти площадь основания цилиндра:
Sосн=π⋅R2=π⋅D24=π⋅a24=π⋅424≈12.56S_{text{осн}}=picdot R^2=frac{picdot D^2}{4}=frac{picdot a^2}{4}=frac{picdot 4^2}{4}approx12.56Sосн=π⋅R2=4π⋅D2=4π⋅a2=4π⋅42≈12.56
Объем цилиндра:
V=Sосн⋅h≈12.56⋅20=251.2 см3V=S_{text{осн}}cdot happrox12.56cdot20=251.2text{ см}^3V=Sосн⋅h≈12.56⋅20=251.2 см3
Ответ
251.2 см3.251.2text{ см}^3.251.2 см3.
Тест по теме «Объем цилиндра»
Источник
Ââåäèòå ðàäèóñ îñíîâàíèÿ è âûñîòó öèëèíäðà | |
| Ðàäèóñ: | |
| Âûñîòà: | |
Öèëèíäð – ãåîìåòðè÷åñêîå òåëî, êîòîðîå ïîëó÷àåòñÿ ïðè âðàùåíèè ïðÿìîóãîëüíèêà âîêðóã åãî ñòîðîíû. Ôîðìóëà îáúåìà öèëèíäðà: , ãäå R – ðàäèóñ îñíîâàíèé, h – âûñîòà öèëèíäðà | |
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
Ìû â ñîöñåòÿõ Ïðèñîåäèíÿéòåñü! Íàøëè îøèáêó? Åñòü ïðåäëîæåíèÿ? Ñîîáùèòå íàì |
Ýòîò êàëüêóëÿòîð ìîæíî âñòàâèòü íà ñàéò, â áëîã Ñîçäàäèì êàëüêóëÿòîð äëÿ âàñ |
Источник
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задание
1
#3043
Уровень задания: Равен ЕГЭ
Радиус первого шара в (5) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?
Площадь поверхности шара радиуса (R) ищется по формуле (S=4pi R^2). Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как [dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2}] Так как радиус первого шара больше радиуса второго шара в 5 раз, то (R_1=5R_2). Следовательно, [dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25.] Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.
Ответ: 25
Задание
2
#3046
Уровень задания: Равен ЕГЭ
Даны два конуса. Радиус второго конуса в (3) раза больше радиуса первого конуса, а высота второго конуса в (6) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен (18).
Объем конуса с высотой (h) и радиусом основания (R) вычисляется по формуле (V=frac13pi R^2h). Следовательно, объем первого конуса относится к объему второго конуса как [dfrac{V_1}{18}=dfrac{V_1}{V_2}=
dfrac{frac13pi ,R_1^2,h_1}{frac13 pi
,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot
dfrac{h_1}{h_2}] Так как радиус второго в 3 раза больше радиуса первого, то (R_2=3R_1). Так как высота второго в 6 раз меньше высоты первого, то (h_1=6h_2). Следовательно, [dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}=
dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot
18=12.]
Ответ: 12
Задание
3
#3048
Уровень задания: Равен ЕГЭ
Даны два конуса: (K_1) и (K_2). Площадь полной поверхности (K_1) относится к площади полной поверхности (K_2) как (4:1). Известно, что радиус (K_1) в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2). Найдите отношение образующей (K_2) к образующей (K_1).
Площадь полной поверхности конуса с образующей (l) и радиусом основания (R) ищется по формуле (S=pi R (R+l)). Тогда площадь полной поверхности (K_1) относится к площади полной поверхности (K_2) как [dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)}] Из условия следует, что (R_1=4l_1), (R_2=frac12R_1=2l_1), следовательно, [dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)}
quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5]
Ответ: 0,5
Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в (343) раза больше объема второго шара?
Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}=
left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad
dfrac{R_1}{R_2}=sqrt[3]{343}=7.] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.
Ответ: 7
Задание
5
#3051
Уровень задания: Равен ЕГЭ
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.
Пусть буквы (a), (b) и (c) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле (V=abc). Следовательно, объем первого параллелепипеда относится к объему второго как [dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2}] Из условия следует, что (a_1=7a_2), (b_2=2b_1), (c_1=3c_2). Тогда [dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}=
dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot
2}{21}=10.]
Ответ: 10
Задание
6
#3049
Уровень задания: Равен ЕГЭ
Площадь боковой поверхности первого цилиндра равна (16). Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.
Площадь боковой поверхности цилиндра с высотой (H) и радиусом основания (R) ищется по формуле (S=2pi RH). Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как [dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}=
dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2}] Из условия следует, что (R_2=4R_1), (H_1=5H_2), значит, [dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}=
dfrac14cdot 5=dfrac54] Следовательно, [S_2=dfrac{16cdot 4}5=12,8.]
Ответ: 12,8
Задание
7
#3047
Уровень задания: Равен ЕГЭ
Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как (3:7). Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как (15:7).
Площадь боковой поверхности конуса с образующей (l) и радиусом основания (R) ищется по формуле (S=pi Rl). Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как [dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2}] Так как радиус первого конуса относится к радиусу второго как (15:7), то есть (frac{R_1}{R_2}=frac{15}7), то [dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad
dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2.]
Ответ: 0,2
Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.
Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.
Базовая информация
Объем геометрической фигуры — это количественная характеристика пространства, которое занимает тело. Она определяется его формой и размерами.
Чтобы задачи на вычисление объемов геометрических фигур не вызывали затруднений, рекомендуем освежить в памяти основные формулы.
- Объем куба равняется кубу длины его грани.
- Объем призмы равняется произведению площади основания фигуры на высоту.
Чтобы его рассчитать, воспользуйтесь следующий формулой: V = So h, где V — объем призмы, So — площадь ее основания, h — ее высота. - Объем прямоугольного параллелепипеда равняется произведению его длины, ширины и высоты.
Формула для его расчета: V = a · b · h, где a — длина,
b — ширина, h — высота. - Объем пирамиды равняется трети от произведения площади ее основания на высоту.
- Объем цилиндра равняется произведению площади его основания на высоту.
Формулы для его расчета:
Для его расчета используется формула: V = a3, где V — объем куба,
a — длина его грани.
Рассчитать его можно по формуле:
V =
1/3
So· h ,
где V — объем пирамиды, So — площадь основания пирамиды, h — длина высоты пирамиды.
V =
π R2 h
V =
So h
Где V — объем цилиндра, So — площадь основания цилиндра, R — радиус цилиндра, h — высота цилиндра, π = 3.141592.
Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?
Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.
Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.
Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.
Источник