Формула расчета объема сосуда

Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 — интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 — интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 — интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
Ôîðìóëà îáúåìà êóáà, øàðà, ïèðàìèäû, ïàðàëëåëîãðàììà, öèëèíäðà, òåòðàýäðà, êîíóñà, ïðèçìû è îáúåìû äðóãèõ ãåîìåòðè÷åñêèõ ôèãóð.
Ôîðìóëà îáúåìà íåîáõîäèìà äëÿ âû÷èñëåíèÿ ïàðàìåòðîâ è õàðàêòåðèñòèê ãåîìåòðè÷åñêîé ôèãóðû.
Îáúåì ôèãóðû – ýòî êîëè÷åñòâåííàÿ õàðàêòåðèñòèêà ïðîñòðàíñòâà, çàíèìàåìîãî òåëîì èëè âåùåñòâîì.  ïðîñòåéøèõ ñëó÷àÿõ îáú¸ì èçìåðÿåòñÿ ÷èñëîì óìåùàþùèõñÿ â òåëå åäèíè÷íûõ êóáîâ, ò. å. êóáîâ ñ ðåáðîì, ðàâíûì åäèíèöå äëèíû. Îáú¸ì òåëà èëè âìåñòèìîñòü ñîñóäà îïðåäåëÿåòñÿ åãî ôîðìîé è ëèíåéíûìè ðàçìåðàìè.
| Ôèãóðà | Ôîðìóëà | ×åðòåæ |
|---|---|---|
Ïàðàëëåëåïèïåä. Îáúåì ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà ðàâåí ïðîèçâåäåíèþ ïëîùàäè îñíîâàíèÿ íà âûñîòó. | V= SH= abh |
|
Öèëèíäð. Îáúåì öèëèíäðà ðàâåí ïðîèçâåäåíèþ ïëîùàäè îñíîâàíèÿ íà âûñîòó. Îáúåì öèëèíäðà ðàâåí ïðîèçâåäåíèþ ÷èñëà ïè (3.1415) íà êâàäðàò ðàäèóñà îñíîâàíèÿ íà âûñîòó. | V = Sh, V = πr2h |
|
Ïèðàìèäà. Îáúåì ïèðàìèäû ðàâåí îäíîé òðåòè ïðîèçâåäåíèÿ ïëîùàäè îñíîâàíèÿ S (ABCDE) íà âûñîòó h (OS). | V = 1/3*Sh |
|
Ïðàâèëüíàÿ ïèðàìèäà — ýòî ïèðàìèäà, â îñíîâàíèè, êîòîðîé ëåæèò ïðàâèëüíûé ìíîãîóãîëüíèê, à âûñîòà ïðîõîäèò ÷åðåç öåíòð âïèñàííîé îêðóæíîñòè â îñíîâàíèå. |
|
|
Ïðàâèëüíàÿ òðåóãîëüíàÿ ïèðàìèäà — ýòî ïèðàìèäà, ó êîòîðîé îñíîâàíèåì ÿâëÿåòñÿ ðàâíîñòîðîííèé òðåóãîëüíèê è ãðàíè ðàâíûå ðàâíîáåäðåííûå òðåóãîëüíèêè. | V = ha2/4√3 |
|
Ïðàâèëüíàÿ ÷åòûðåõóãîëüíàÿ ïèðàìèäà — ýòî ïèðàìèäà, ó êîòîðîé îñíîâàíèåì ÿâëÿåòñÿ êâàäðàò è ãðàíè ðàâíûå ðàâíîáåäðåííûå òðåóãîëüíèêè. | V = 1/3*ha2 | |
Òåòðàýäð — ýòî ïèðàìèäà, ó êîòîðîé âñå ãðàíè — ðàâíîñòîðîííèå òðåóãîëüíèêè. | V = (a3√2)/12 |
|
Óñå÷åííàÿ ïèðàìèäà. Îáúåì óñå÷åííîé ïèðàìèäû ðàâåí îäíîé òðåòè ïðîèçâåäåíèÿ âûñîòû h (OS) íà ñóììó ïëîùàäåé âåðõíåãî îñíîâàíèÿ S1(abcde), íèæíåãî îñíîâàíèÿ óñå÷åííîé ïèðàìèäû S2 (ABCDE) è ñðåäíåé ïðîïîðöèîíàëüíîé ìåæäó íèìè. | V= 1/3 h (S1+ √S1S2 + S2) |
|
Êóá. Âû÷èñëèòü îáúåì êóáà ëåãêî – íóæíî ïåðåìíîæèòü äëèíó, øèðèíó è âûñîòó. Òàê êàê ó êóáà äëèíà ðàâíà øèðèíå è ðàâíà âûñîòå, òî îáúåì êóáà ðàâåí s3. | V = s3 |
|
Êîíóñ — ýòî òåëî â åâêëèäîâîì ïðîñòðàíñòâå, ïîëó÷åííîå îáúåäèíåíèåì âñåõ ëó÷åé, èñõîäÿùèõ èç îäíîé òî÷êè (âåðøèíû êîíóñà) è ïðîõîäÿùèõ ÷åðåç ïëîñêóþ ïîâåðõíîñòü. | V = 1/3 πR2H |
|
Óñå÷åííûé êîíóñ ïîëó÷èòñÿ, åñëè â êîíóñå ïðîâåñòè ñå÷åíèå, ïàðàëëåëüíîå îñíîâàíèþ. | V = 1/3 πh (R2 + Rr + r2) |
|
Øàð. Îáúåì øàðà â ïîëòîðà ðàçà ìåíüøå, ÷åì îáúåì îïèñàííîãî âîêðóã íåãî öèëèíäðà. | V = 4/3 πr3 |
|
Ïðèçìà. Îáúåì ïðèçìû ðàâåí ïðîèçâåäåíèþ ïëîùàäè îñíîâàíèÿ ïðèçìû, íà âûñîòó. | V = So h |
|
Ñåêòîð øàðà. Îáúåì øàðîâîãî ñåêòîðà ðàâåí îáúåìó ïèðàìèäû, îñíîâàíèå êîòîðîé èìååò òó æå ïëîùàäü, ÷òî è âûðåçàåìàÿ ñåêòîðîì ÷àñòü øàðîâîé ïîâåðõíîñòè, à âûñîòà ðàâíà ðàäèóñó øàðà. | V = 1/3 R S = 2/3 π R2 h |
|
Øàðîâîé ñëîé — ýòî ÷àñòü øàðà, çàêëþ÷åííàÿ ìåæäó äâóìÿ ñåêóùèìè ïàðàëëåëüíûìè ïëîñêîñòÿìè. | V = 1/6 π h3 + 1/2 π (r12+ r22) h |
|
Ñåãìåíò øàðà – ýòî ÷àñòü øàðà, îñåêàåìàÿ îò íåãî êàêîé-íèáóäü ïëîñêîñòüþ, íàçûâàåòñÿ øàðîâûì èëè ñôåðè÷åñêèì ñåãìåíòîì | V = π h2 ( R – 1/3 h) |  |
Äîïîëíèòåëüíûå ìàòåðèàëû ïî òåìå: Ôîðìóëà îáúåìà.
| |||||||||||||
| |||||||||||||
|
| ||||||||||||
Источник
1. Расчет объема куба

a – сторона куба
Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
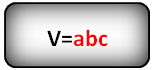
3. Формула для вычисления объема шара, сферы

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

4. Как вычислить объем цилиндра ?
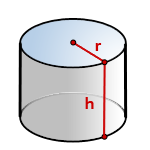
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

5. Как найти объем конуса ?
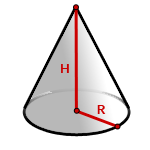
R – радиус основания
H – высота конуса
π ≈ 3.14
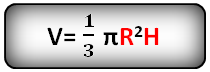
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
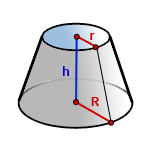
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

8. Объем правильного тетраэдра
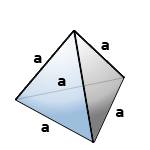
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
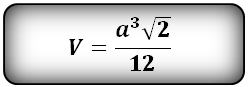
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
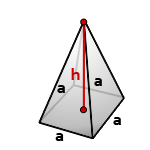
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
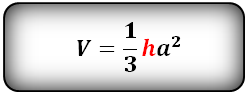
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
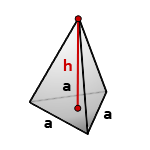
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
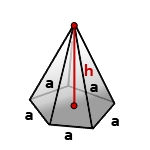
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
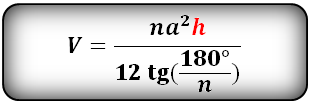
12. Расчет объема пирамиды
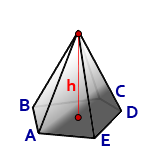
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
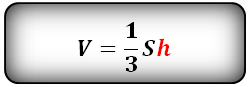
13. Расчёт объёма усечённой пирамиды
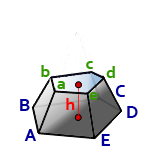
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

14. Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
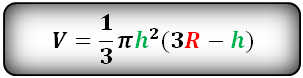
15. Объем шарового сектора
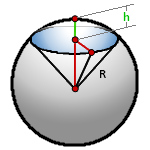
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

16. Объем шарового слоя
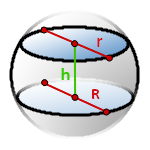
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
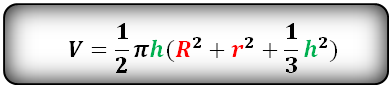
Источник
Инструкция для онлайн калькулятора по расчету объема в прямоугольных емкостях (типа аквариума)

Все величины указываем в мм
H — Уровень жидкости.
Y — Резервуар в высоту.
L — Длина емкости.
X — Резервуар в ширину.
Данная программа выполняет вычисления объема жидкости в различных по размеру емкостях прямоугольной формы, также поможет рассчитать площадь поверхности резервуара, свободный и общий объем.
По итогам вычисления Вы узнаете:
- Полную площадь резервуара;
- Площадь боковой поверхности;
- Площадь дна;
- Свободный объем;
- Количество жидкости;
- Объем емкости.
Технология расчета количества жидкости в резервуарах разной формы
Когда емкость неправильной геометрической формы (к примеру, в виде пирамиды, параллелепипеда, прямоугольника и т.д.) необходимо в первую очередь выполнить измерения внутренних линейных размеров и только после этого произвести вычисления.
Расчет объема жидкости в прямоугольной емкости небольших размеров, вручную можно выполнить следующим образом. Необходимо залить жидкостью весь резервуар до краев. Тогда объем воды в данном случае станет равен объему резервуара. Далее следует слить аккуратно всю воду в отдельные емкости. К примеру, в специальный резервуар правильной геометрической формы или измеряющий цилиндр. По измерительной шкале Вы сможете визуально определить объем Вашего резервуара. Для расчета количества жидкости в прямоугольной емкости Вам лучше всего воспользоваться нашей онлайн программой, которая быстро и точно выполнить все вычисления.
Если резервуар большого размера, и в ручную невозможно измерить количество жидкости, то можно использовать формулу массы газа с молярной известной массой. К примеру, масса азота М=0,028 кг/моль. Данные вычисления возможны, когда резервуар можно плотно закрыть (герметически). Теперь при помощи термометра измеряем температуру внутри резервуара, и манометром внутреннее давление. Температура должна быть выражена в Кельвинах, а давление в Паскалях. Вычислить объем внутреннего газа можно следующей формуле (V=(m∙R∙T)/( M∙P)). То есть массу газа (m) умножаем на температуру его (Т) и газовую константу (R). Далее полученный результат следует разделить на давление газа (Р) и молярную массу (М). Объем будет выражен в м³.
Как вычислить и узнать объем аквариума по размерам самостоятельно
Аквариумы – стеклянные сосуды, которые заполняют чистой водой до определенного уровня. Многие собственники аквариума неоднократно задумывались, какого объема их резервуар, как можно выполнить вычисления. Самый простой и надежный метод, это воспользоваться рулеткой и замерять все необходимые параметры, которые следует вбить в соответствующие ячейки нашего калькулятора, и Вы сразу же получите готовый результат.
Однако существует и другой способ определения объема аквариума, который заключается в более долгом процессе, использования литровой банки, постепенно заполняя всю емкость до соответствующего уровня.
Третий метод вычисления объема аквариума, это специальная формула. Замеряем глубину резервуара, высоту и ширину в сантиметрах. К примеру, у нас получились следующие параметры: глубина – 50 см, высота – 60 см и ширина – 100 см. Согласно этим размерами, объем аквариума рассчитывается по формуле (V=X*Y*H) или 100х50х60=3000000 см³. Далее нам необходимо полученный результат перевести в литры. Для этого готовое значение умножаем на 0,001. Отсюда следует — 0,001х3000000 сантиметров, и получаем, объем нашего резервуара составит 300 литров. Это мы вычислили полную вместительность емкости, далее необходимо вычислить реальный уровень воды.
Каждый аквариум наполняют значительно ниже, чем его реальная высота, дабы избежать перелива воды, чтобы закрыть крышкой с учетом стяжки. К примеру, когда наш аквариум высотой 60 сантиметров, тогда вклеенные стяжки будут располагаться на 3-5 сантиметров ниже. При нашем размере в 60 сантиметров, чуть менее 10% объема емкости припадает на 5-сантиметровые стяжки. Отсюда мы можем вычислить реальный объем 300 л – 10%=270 л.
Важно! Следует отнять несколько процентов учитывая объем стекол, размеры аквариума или любой другой емкости снимаем с наружной стороны (без учета толщины стекол).
Отсюда объем нашего резервуара будет равен 260 литров.
Источник















