Гармонические колебания жидкости в сообщающихся сосудах
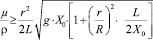
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Байджанов Д.О.
3
Кропачев П.А.
3
Бюнау Е.К.
1
Малышев О.А.
2
Дивак Л.А.
3
1 ОАО «ГАЗПРОМ-ВНИИГАЗ»
2 ЗАО «СТРИМЕР-ЦЕНТР»
3 Карагандинский государственный технический университет – вуз Первого Президента РК
Настоящая статья посвящена вопросу фундаментального развития техники физических измерений, а именно: совершенствованию измерений вязкости жидкостей в сообщающихся сосудах, учитывающих свободное, как апериодическое, так и колебательное движение жидкости при разных температурах. Актуальной задачей измерений вязкости жидкостей при различных температурах является возможность экспериментального подтверждения теоретических расчетов с высокой степенью точности. Известны и широко применяются стеклянные капиллярные вискозиметры, в расчётную схему которых положена формула Пуазейля, связывающая расход и перепад давления жидкости с её вязкостью в условиях ламинарного течения в круглой трубе известной геометрии. В данной работе рассматриваются жидкости, ламинарное течение которых в круглой трубе, так же как в стеклянных вискозиметрах, точно или с некоторым приближением удовлетворяют уравнению Пуазейля. Полученные аналитические зависимости, подтвержденные опытным путем, могут быть использованы при проектировании технологических установок и измерительных приборов, в которых используется принцип сообщающихся сосудов.
жидкость
апериодический процесс
свободные колебания
измерения
вязкость
сила вязкого трения
вискозиметр
1. Барботажный объемометрический метод контроля вязкости жидкостей. Мордасов М.М., Козадаева М.М., Баршутина М.Н. Заводская лаборатория. Диагностика материалов. – 2008. – Т. 74. № 12. – С. 11–12.
2. Бесконтактный неразрушающий аэрогидродинамический контроль вязкости жидкостей. Мордасов М.М., Савенков А.П. Заводская лаборатория. Диагностика материалов. – 2008. – Т. 74. № 2. – С. 22–25.
3. Вискозиметр с двумя восходящими трубками и одним капилляром (варианты) и способ измерения вязкости жидкостей (варианты). Кенсей К., Хогенауер В.Н., Чо Ю., Ким С. Патент на изобретение RUS 2256164 от 12.10.2000.
4. Измерение динамической вязкости жидкостей по затуханию колебаний камертона. Жданов А.Г., Пятаков А.П. Физическое образование в ВУЗах. – 2002. – Т. 8. № 4. – С. 117–126.
5. Контроль вязкости жидкости по времени формирования пузырька газа с постоянной массой. Голосницкая М.М., Мордасов М.М., Савенков А.П. Заводская лаборатория. Диагностика материалов. – 2012. – Т. 78. № 3. – С. 34–38.
6. Простой прибор для измерения поверхностного натяжения и вязкости жидкостей. Singh M. Приборы и техника эксперимента. – 2005. – № 2. – С. 143–145.
7. Способ измерения вязкости жидкостей. Савенков А.П., Мордасов М.М. патент на изобретение RUS 2417363 от 09.03.2010.
8. Способ измерения вязкости Ньютоновских жидкостей. Алашкевич Ю.Д., Ковалев В.И., Ерофеева А.А. Патент на изобретение RUS 2441217 от 28.10.2010.
9. Способ контроля вязкости жидкостей. Баршутина М.Н., Козадаева М.М., Мордасов Д.М., Мордасов М.М. патент на изобретение RUS 2368886 от 29.11.2007.
10. Способ одновременного измерения плотности и вязкости жидкости. Тетерин Е.П., Потехин Д.С., Тарасов И.Е. Патент на изобретение RUS 2247357 от 10.11.2003.
11. Тимошенко С.П. Колебания в инженерном деле. – М.: НАУКА, 1967.
12. Фрайфелдер Д. Физическая химия.- М.: МИР, 1980.
13. Abbas K.A., Abdulkarim S.M., Saleh A.M. and Ebrahimian M. Suitability of viscosity measurement methods for liquid food variety and applicability in food industry – A review. Journal: Food, Agriculture and Environment (JFAE). Received 18 July 2009, accepted 8 October 2009.
14. Behic Mert, Hartono Sumali, Osvaldo Y. Campanella. A new method to determine viscosity of liquids using vibration principles. Rheologica Acta. November 2003, Volume 42, Issue 6, pp 534–543.
15. Ben-Yuan Lin. Measurement of Viscosity in a Vertical Falling Ball Viscometer. American Laboratory. October 27, 2008.
16. Coles, D. (1965), Transition in circular Couette flow, J. of Fluid Mechanics, 21, 91. DOI: 10.1017/S0022112065000241.
17. https://www.highexpert.ru/content/liquids/eg_gl.html.
18. Janet L. Lane and Kenneth O. Henderson. Viscosity Measurement. So Easy, Yet So Difficult. Standardization News. June. 2004.
19. Patent USA 6152888. Viscosity measuring apparatus and method of use. 11.28.2000.
20. Patent USA 6805674. Viscosity measuring apparatus and method of use. 19.10.2004.
21. Patent USA 7578782. Methods and systems for determining a viscosity of a fluid. 08.25.2009.
22. Wu Jian and Luo Rongmo. Standard for High Viscosity and Multiphase Liquid Flow Measurement. 16th International Congress of Metrology, 02009 (2013).
Наука начинается с тех пор, как начинают измерять.
Д.И. Менделеев
Под апериодическим движением рассматривается переходный процесс в динамической системе, при котором выходная величина, характеризующая переход системы от одного состояния к другому, либо монотонно стремится к установившемуся значению, либо имеет один экстремум. Теоретически может длиться бесконечно большое время.
Не только в основе существования и развития самой науки, но и в развитии технологий всех промышленных отраслей лежат измерения, которые в условиях современной конкурентной среды последовательно проходят путь своего развития от исторических технологий до технологий настоящего и будущего, появляющихся в результате современных научных исследований [1–10, 13–16, 18–21].
Актуальной задачей измерений вязкости жидкостей при различных температурах является возможность экспериментального подтверждения теоретических расчетов с высокой степенью точности. Известны [12] и широко применяются стеклянные капиллярные вискозиметры, в расчётную схему которых положена формула Пуазейля, связывающая расход и перепад давления жидкости с её вязкостью в условиях ламинарного течения в круглой трубе известной геометрии.
В подобных приборах о вязкости исследуемой жидкости судят по времени её перетекания из одного сосуда в другой. Внутренний диаметр стеклянного капилляра длиной 100–200 мм такого вискозиметра составляет обычно 0,1 … 0,3 мм, поэтому с его помощью может быть измерена вязкость исключительно чистых и однородных жидкостей, не содержащих включений, соизмеримых с просветом капилляра.
Возможность калибровки по жидкостям с известными значениями плотности и вязкости обеспечила этим конструкциям широкое применение.
Конструкция таких вискозиметров показана на рис. 1.
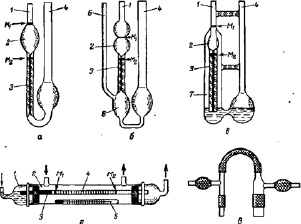
Рис. 1. Вискозиметры Оствальда (а), Уббелоде или ВПЖ-1 (б) Мартина (в). Микровискозиметр (г) и насадка Эппельбея (д)
Основная идея, лежащая в основе таких конструкций – это нестационарное течение (предположительно «ньютоновской») жидкости в сообщающихся сосудах. Она определяет все достоинства и недостатки схемы.
Подкупающая (внешняя) простота и изя щество конструкции таких вискозиметров, в особенности схемы Оствальда, вызывает желание рассмотреть расчётную схему такого прибора без ограничений, связанных с размерами трубки (уже не капиллярной, а произвольного диаметра), вязкостью и плотностью исследуемой жидкости, её количеством и качеством.
Под качеством здесь следует понимать возможность содержания в жидкости включений, способных легко «проскакивать» в просвет трубки.
В данной работе рассматриваются жидкости, ламинарное течение которых в круглой трубе, так же как в стеклянных вискозиметрах, точно или с некоторым приближением удовлетворяют уравнению Пуазейля.
Расчётная схема, в виде одинаковых сосудов 1 и 2 радиусом R, гидравлически соединённых горизонтальной трубкой 3 длиной L и радиусом r, показана на рис. 2.
Рис. 2. Расчетная схема вискозиметра
На рис. 2 показаны: жидкость, выведенная тем или иным способом из равновесия так, что она из сосуда 1 перетекает в сосуд 2 под действием только силы тяжести; X0 – уровень, соответствующий положению равновесия жидкости в сосудах 1 и 2; X(t) – текущее отклонения уровня жидкости от положения равновесия – понижается в сосуде 1 и повышается в сосуде 2.
Масса жидкости, размещённой в сосудах 1 и 2 и трубке 3, равна
, (1)
где ρ, – плотность жидкости; R, м – радиус сосудов 1 и 2; r, L, м – радиус и длина трубки.
За координату, характеризующую изменения сил в системе, примем X(t) – текущее отклонение уровня жидкости в сосудах 1 и 2 от положения равновесия.
В неустановившемся движении перетекания участвует вся жидкость массы m0.
Поэтому силу инерции, препятствующую изменению скорости восстановления равновесия жидкости, представим в виде
Н. (2)
Сила, стремящаяся вернуть систему в состояние равновесия, равна всей неуравновешенной части жидкости в виде
Н, (3)
где g, – ускорение силы тяжести.
Полагаем, что силой, препятствующей перетеканию жидкости их сосуда 1 в сосуд 2, является сила вязкого трения в трубке 3.
Для её аналитического представления рассмотрим уравнение Пуазейля
, (4)
где Q, – объёмный расход жидкости c вязкостью µ, Па•с;
, Па – перепад давлений жидкости в начале и в конце трубки.
Из физических соображений (условие неразрывности) объёмный расход жидкости через трубку 3 равен убыли её объёма во времени в сосуде 1 и соответственно увеличению объёма в сосуде 2, то есть характеризует силу вязкого трения, препятствующей перемещению неуравновешенной массы жидкости со скоростью изменения уровня через трубку 3.
,. (5)
Произведение
, H. (6)
Из уравнения (4) с учётом (5) и (6) следует выражение для силы вязкого трения, препятствующего достижению положения равновесия в виде
, H. (7)
Таким образом, сумма выражений (2), (3) и (7) представляет собой дифференциальное уравнение свободных колебаний уровня жидкости в сообщающихся сосудах в виде
+ ? +. (8)
Разделив слагаемые уравнения (8) на m0, получим дифференциальное уравнение свободных колебаний системы с одной степенью свободы в стандартном виде
= 0. (9)
Коэффициент n, характеризующий диссипативные свойства колебательной системы выражается через вышеуказанные параметры и имеет вид
. (10)
Коэффициент ω характеризует собственную частоту колебаний недемпфированной колебательной системы (µ = 0) в виде
,. (11)
В соответствии с [11], для случая и начальных условий при t = 0, X (0) = h0 и (0) = 0 решение уравнения (9) имеет вид затухающих колебаний
, (12)
где h0 –высота начального подъёма уровня жидкости в сосуде 1;
.
Выражение для скорости изменения уровня жидкости для тех же начальных условий имеет вид
. (13)
Для случая и начальных условий при t = 0, X (0) = h0 и (0) = 0 решение уравнения (9) имеет апериодический характер
(14)
где – действительные отрицательные корни характеристического уравнения, вычисляемые по формуле
. (15)
Выражение для скорости изменения уровня жидкости для тех же начальных условий в этом случае имеет вид
. (16)
Из соотношения величин (10) и (11) может быть составлено условие, например, отсутствия периодических движений жидкости в сообщающихся сосудах в виде неравенства
. (17)
В левой части неравенства (17) отношение динамической вязкости µ к плотности ρ представляет собой кинематическую вязкость жидкости, а правая часть содержит размеры r, L, X0, R, соответствующие рис. 2.
Полученные выше аналитические зависимости могут быть использованы при проектировании технологических установок и измерительных приборов, в которых используется принцип сообщающихся сосудов.
Эффективность применения неочевидного условия (17) можно показать на примере выбора конструктивных размеров устройства по схеме рис. 2, в которой для одной и той же жидкости при разных температурах возможны как апериодическое, так и колебательное движение.
Покажем это на примере этиленгликоля (HO-CH2CH2-OH), широко используемого в качестве антифриза.
На основании табличных данных, приведенных в [17], зависимость кинематической вязкости этиленгликоля от температуры показана на графике рис. 3.
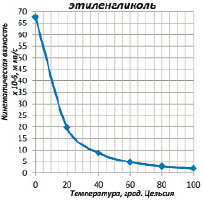
Рис. 3. Зависимость кинематической вязкости этиленгликоля от температуры
Как видно из графика на рис. 3, при увеличении температуры от 0 до + 100 °С кинематическая вязкость этиленгликоля уменьшается в 33 раза.
Выберем значения размеров, показанных на рис. 2, R = 0,02 м, r = 0,02 м, X0 = 0,1 м, h0 = 0,05 м, L = 0,07 м, удовлетворяющие условиям
,
и ,
где крайние значения соответствуют кинематической вязкости этиленгликоля при + 5 °С и + 100 °С соответственно.
Для «холодного» этиленгликоля апериодический закон изменения уровня и скорости его изменения во времени показан на рисунках 4 и 5.
Для «горячего» этиленгликоля колебательный закон изменения уровня и его скорости во времени показан на рис. 6 и 7.
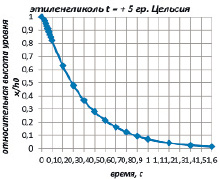
Рис. 4. График изменения уровня жидкости в сосуде во времени
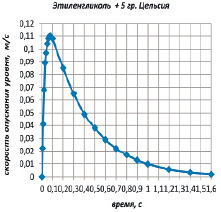
Рис. 5. График скорости изменения уровня жидкости в сосуде во времени
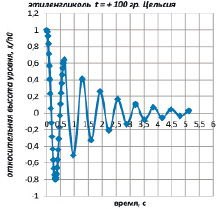
Рис. 6. График изменения уровня жидкости в сосуде во времени
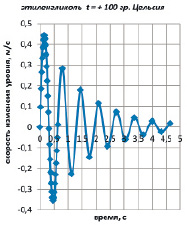
Рис. 7. График скорости изменения уровня жидкости в сосуде во времени
Полученные выше аналитические зависимости, подтвержденные опытным путем, могут быть использованы при проектировании технологических установок и измерительных приборов, в которых используется принцип сообщающихся сосудов, а рассмотренный пример с колебаниями этиленгликоля в сообщающихся сосудах представлен в учебном пособии по изучению основ гидравлики и теории колебаний для студентов, магистрантов, аспирантов и докторантов.
Библиографическая ссылка
Байджанов Д.О., Кропачев П.А., Бюнау Е.К., Малышев О.А., Дивак Л.А. СВОБОДНЫЕ КОЛЕБАНИЯ ВЯЗКОЙ ЖИДКОСТИ В СООБЩАЮЩИХСЯ СОСУДАХ // Фундаментальные исследования. – 2014. – № 9-10. – С. 2157-2163;
URL: https://fundamental-research.ru/ru/article/view?id=35287 (дата обращения: 03.03.2021).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Источник
Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
