Газ адиабатически вытекает из сосуда через трубку
| Другие темы раздела | |
| Термодинамика и МКТ График изотермы в осях U T https://www.cyberforum.ru/ mkt-thermodynamics/ thread2635698.html Доброго времени суток, форумчане! Сломал голову и затер гугл до дыр, а никак не получается найти график изотермического процесса ИГ в плоскости UT, где U – как и полагается, внутренняя энергия газа. … | Термодинамика и МКТ Определите массу газа вытекающего за 1 секунду через капилляр, если наружное давление составляет 760 ммртст 2)Кислород вытекает из сосуда, где он находится под давлением p1= (1000 + 50*N) ммрт. ст. через капилляр радиуса a= 0,01*N(мм). Определите массу газа вытекающего за 1 секунду через капилляр, если… |
| Определите среднюю по сечению трубки скорость течения газа Термодинамика и МКТ Всем привет, огромная просьба помочь с решением двух задач. Их условия: 1)Азот вытекает из сосуда через горизонтальную трубку. Длина трубки l, радиус a= 0,01*N(мм). Определите среднюю по сечению… | Термодинамика и МКТ Работа при адиабатическом расширении Здравствуйте ,поясните ошибку… При обратимом адиабатическом расширении азота (N2) массой m = 0.4 кг, его температура понижается на ΔT = 4 К. Определить работу А, совершаемую газом при расширении…. https://www.cyberforum.ru/ mkt-thermodynamics/ thread2631641.html |
| Термодинамика и МКТ Почему при наличии двух источников тепла единственно возможным обратимым циклом является цикл Карно https://www.cyberforum.ru/ mkt-thermodynamics/ thread2631069.html Почему при наличии двух источников тепла единственно возможным обратимым циклом является цикл Карно? Заранее огромное спасибо! | Термодинамика и МКТ Каково давление на высоте 3 км, если предположить, что атмосфера изотермическая (t = 20°C) На некоторой планете ускорение на поверхности составляет 10 м/с2, давление на поверхности планеты составляет 2 атм, а на высоте 1 км – 1 атм. Каково давление на высоте 3 км, если … |
| При изобарном нагревании идеального газа была получена зависимость V от T Термодинамика и МКТ Помогите пожалуйста решить такое задание: При изобарном нагревании идеального газа была получена зависимость V от T, изображенная на рисунке 2. Что происходило с газом? Представить этот процесс на… | Термодинамика и МКТ Вычислить молярную теплоёмкость идеального газа для политропического процесса Целый День решаю, вроде бы приблизился, но что-то не так. нужна помощь;Вычислить молярную теплоёмкость идеального газа для политропического процесса, в котором давление изменяется пропорционально… https://www.cyberforum.ru/ mkt-thermodynamics/ thread2623026.html |
| Термодинамика и МКТ Найти температуру воздуха после сжатия https://www.cyberforum.ru/ mkt-thermodynamics/ thread2622290.html Объём воздуха в трубке «воздушного огнива» уменьшается в 10 раз адиабатически. Найти температуру воздуха после сжатия, если начальная температура воздуха была 17 градусов Цельсия. | Термодинамика и МКТ Какое давление Р установится в сосуде при изотермическом увеличении его объема в η = 4.1 раз Добрый день. Прошу помощи в решении задачи. В замкнутом сосуде объемом V = 7.6 м3 при t = 20 градусов Цельсия находится v= 1 моль жидкой воды и насыщенный пар. Какое давление Р установится в сосуде… https://www.cyberforum.ru/ mkt-thermodynamics/ thread2621361.html |
1 / 1 / 0 Регистрация: 21.12.2019 Сообщений: 35 | |
09.05.2020, 14:05 [ТС] |
|
09.05.2020, 14:05. Просмотров 1055. Ответов 11 Ответ Сообщение от Hant Надо было написать, что давление равно 1,01*105 Па. Спасибо большое за помощь и версии ! Но все таки необходима тактичность) Вычислил исходит Вернуться к обсуждению: | |
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 | 09.05.2020, 14:05 |
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь. Что я делаю не так? Что я делаю не так? Что я делаю не так Что делаю не так Что я делаю не так? Начав тренировку спортсмен первый день пробежал… Что делаю не так? 0 |
Источник
Задача 227
Воздух в комнате нагрели с температуры до T. При этом давление воздуха осталось постоянным. Изменилась ли внутренняя энергия воздуха в комнате?
Ответ:
Задача 228
В теплоизолированном сосуде при температуре 800 К находится 1 моль углекислого газа и один моль водорода. Происходит химическая реакция
Во сколько раз возрастет давление в сосуде после окончания реакции?
Ответ: в 2 раза;
Задача 229
В длинной теплоизолированной трубе находятся теплоизолированные поршни массы , между которыми в объеме находится при давлении одноатомный газ. Поршни отпускают. Определите их максимальные скорости, если масса газа много меньше массы каждого поршня.
Ответ:
 Задача 230
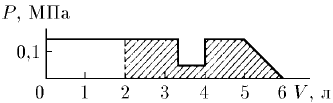
Задача 230
На рисунке дан график зависимости давления от объема. Найдите работу газа при расширении его от 2 до 6 л.
Ответ:
Задача 231
Один моль водорода, имевший температуру 0° С, нагревается при постоянном давлении. Какое количество теплоты необходимо сообщить газу, чтобы его объем удвоился? Какая работа при этом будет совершена газом?
Ответ:
Задача 232
Сжатый воздух поступает в цилиндр пневматического двигателя из магистрали постоянного давления при температуре . Затем доступ в цилиндр воздуха из магистрали перекрывается. Оказавшийся в цилиндре воздух продолжает двигать поршень, расширяясь без теплообмена, пока давление не упадет до атмосферного, а температура до . Затем поршень движется назад и через открывшийся клапан вытесняет весь воздух из цилиндра. После этого цикл повторяется. Найдите работу двигателя при расходе им υ молей сжатого воздуха.
Ответ:
 Задача 233
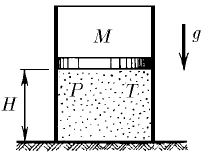
Задача 233
В откачанном пространстве вертикально стоит цилиндрический сосуд. Перекрытый сверху подвижным поршнем массы M. Под поршнем находится одноатомный газ при температуре T и давлении P. Внутреннее сечение цилиндра S, высота части сосуда, внутри которой находится газ, H. Поршень отпустили, и он начал двигаться. Чему равна максимальная скорость, развиваемая поршнем, если газ сжимается изотермически? адиабатически?
Ответ:
Задача 234
Два компрессора адиабатически сжимают двухатомный газ. Сначала работает один компрессор, сжимающий газ от объема до промежуточного объема . Затем сжатый газ охлаждается до первоначальной температуры, после чего начинает работать второй компрессор, сжимающий газ до объема . При каком объеме полная работа обоих компрессоров минимальна и чему она равна? Объемы и считать заданными, начальное давление газа . Работа какого компрессора при оптимальном значении больше?
Ответ:
 Задача 235
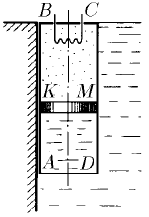
Задача 235
Цилиндр ABCD, закрытый сверху и открытый снизу, прикреплен к стенке бассейна, заполненного водой. В верхней части цилиндра KBCM, находится 1 моль гелия, отделенный от воды поршнем, . Гелий нагревают спиралью. Какое количество теплоты нужно подвести к газу, чтобы поршень опустился на расстояние h? Массой поршня, трением и теплопроводностью пренебречь. Бассейн много больше размеров цилиндра. Плотность воды ρ, сечение цилиндра S. .
Ответ:
Задача 236
Найдите молярную теплоемкость одноатомного газа, расширяющегося по закону . При каких значениях n теплоемкость будет равна нулю, при каких бесконечности?
Ответ:
Истечение газа.
Задача 237
Определите скорость адиабатического истечения смеси двухатомных газов с молярной массой и . Число молекул первого газа в k раз больше числа молекул второго газа. Температура смеси T.
Ответ:
Задача 238
Определите максимальную скорость истечения газа из сопла ракеты, если тяга ракеты создается в результате реакций:
1. ;
2. .
Ответ: и
Задача 239
Газ адиабатически вытекает из сосуда через трубку. Температура газа в сосуде , давление . На выходе из трубки давление газа . Определите скорость газа на выходе из трубки. Молярная масса газа µ, показатель адиабаты γ.
Ответ:
Дата: 2019-04-23, просмотров: 73.
Источник
Для многих технических приложений газодинамики весьма важным случаем является течение газа по трубопроводу переменного сечения без притока или отдачи тепла (т. е. адиаёатно) и без производства работы. В этом случае, когда (для упрощения положим, что и основное уравнение газодинамики преобразуется в уравнение, которое является термодинамическим обобщением уравнения Бернулли:
Здесь в отличие от уравнения Бернулли (§ 49) вместо давления, деленного на плотность, фигурирует теплосодержание; но и очевидно, что для потока несжимаемой жидкости, когда нет необходимости учитывать изменение термодинамического состояния (т. е. когда внутренняя энергия жидкости предполагается постоянной, и когда плотность неизменна), уравнение (4) переходит в уравнение Бернулли.
Из термодинамического обобщения уравнения Бернулли мы видим, что сумма теплосодержания и кинетической энергии газового потока при стационарном адиабатном течении без производства работы одинакова для всех сечений потока.
Течение, при котором скорость газа убывает, а плотность, давление и температура растут, называется течением со сжатием. (Следует подчеркнуть, что здесь слово «сжатие» относится к термодинамическому состоянию потока, к удельному объему газа, а отнюдь не к площади поперечного сечения трубопровода; при не слишком больших начальных скоростях газа в расширяющемся трубопроводе газ затормаживается, кинетическая энергия его уменьшается, а температура и плотность растут, т. е. имеет место течение со сжатием.)
Течение, при котором кинетическая энергия потока растет, а плотность, давление и температура уменьшаются, называется течением с расширением. Рассмотрим оба случая течения в отдельности.
Течение с расширением имеет место, например, при истечении пара из котла или при истечении газа из камеры реактивного двигателя.
При адиабатном течении с расширением прирост кинетической энергии вызывается убылью теплосодержания и падением температуры:
Падение температуры сопровождается уменьшением давления и плотности газа 7; когда расширение газа происходит равновесно, можно воспользоваться уравнением Пуассона
Следовательно,
Здесь согласно уравнению Майера
Представим себе, что из баллона, где давление газа и температура вследствие большого поперечного сечения баллона приближенно можно принять равной нулю), газ адиабатно вытекает через отверстие площадью 5 в резервуар, в котором давление («противодавление») При небольших перепадах давления (когда превышает на несколько процентов или десятков процентов, но не более чем в раза) давление газа в вытекающей струе равно противодавлению В этом случае согласно уравнению (6) скорость истечения определяется формулой
Здесь статическое давление в вытекающей струе.
Весовой расход газа равен произведению площади поперечного сечения отверстия на скорость истечения и на плотность вытекающего газа
По мере уменьшения противодавления давление в вытекающей струе будет уменьшаться, а вместе с ним будет адиабатно уменьшаться по закону Пуассона и плотность вытекающего газа; скорость истечения будет расти.
Весовой расход газа через данное отверстие 5 определяется двумя величинами: плотностью и скоростью истечения газа. Первая из этих величин, с уменьшением противодавления убывает, а вторая, наоборот, растет. Расход газа с уменьшением противодавления первое время увеличивается за счет быстрого увеличения скорости; затем расход замедляется за счет заметного уменьшения плотности и, наконец, становится постоянным: каким бы малым ни было противодавление, расход газа будет иметь одну и ту же величину.
Таким образом, оказывается, что когда противодавление составляет примерно половину давления в баллоне (более точное соотношение указано ниже), то дальнейшее уменьшение противодавления является бесполезным для повышения скорости истечения и расхода газа. В струе устанавливаются некоторые так называемые критические значения скорости истечения, давления, температуры и плотности газа, которые уже более не изменяются, как бы мы дальше ни уменьшали противодавление. Если до этого момента давление на выходе в струе, как было упомянуто выше, оставалось равным противодавлению то с указанного момента при истечении газа с критической скоростью у выходного отверстия устанавливается скачок давления так как уменьшение уже не будет больше вызывать уменьшения
Пусть, например, в баллоне заключен газ под давлением в можно выпускать этот газ в пустоту, в атмосферу или перепускать этот газ в другой баллон, где давление составляет несколько атмосфер; во всех случаях расход газа, скорость его истечения и давление в вытекающей струе будут одинаковы и будут оставаться постоянными до тех пор, пока противодавление не достигнет (при дальнейшем росте противодавления расход и скорость истечения будут уменьшаться).
Можно доказать (см. примечание на стр. 532—533), что отношение давления в баллоне перед истечением к критическому давлению в струе равно:
(для воздуха
Скорость газа, вытекающего из отверстия или из сужающегося насадка, не может быть больше критической скорости:
Понижение температуры в струе при критическом истечении согласно уравнению Пуассона и формуле (8) равно:
Таким образом, стало быть, формулу (9) можно переписать так:
Критическая скорость равна скорости, с которой распространяется звук при имеющейся в струе температуре Тк. Ни при каком сколь угодно большом давлении в баллоне газ не может вытекать из отверстия со скоростью, большей, чем скорость звука.
Когда давление в струе равно критическому давлению, а скорость истечения равна скорости звука, то расход газа С будет иметь наибольшую величину, возможную при начальных термодинамических параметрах газа в баллоне.
Вычисление показывает, что максимальный расход газа при критическом течении определяется формулой
Для воздуха при
Чтобы понять физические причины, обусловливающие существование критических параметров в струе вытекающего газа, представим себе, что противодавление вдруг резко снижено (хотя бы до нуля); если скорость истечения уже достигла перед тем скорости звука, то «весть» об указанном событии никогда не будет передана возникшей звуковой волной разрежения в струю выходящего газа, и, стало быть, это событие не отразится на термодинамическом состоянии газа, вытекающего со скоростью распространения звуковых волн.
Рис. 268.
Регулируя режим течения газа определенным выбором профиля трубопровода, можно использовать избыточное давление, возникающее в струе при критическом истечении, и реализовать скорости течения, превышающие скорость звука Физически эта задача заключается в том, чтобы изыскать условия, при которых неупорядоченное молекулярно-тепловое движение в газе, который уже движется со скоростью звука, частично превратить в упорядоченное движение и, таким образом сообщить массе газа скорость, превышающую критическую скорость истечения. С указанной целью авалем, Стентоном и советским ученым Франклем были разработаны сверхзвуковые сопла (рис» 268).
В сопле Лаваля скорость газа непрерывно растет , в сужающейся части сопла скорость возрастает от нуля до звуковой величины (рис. 269), в расширяющейся части сопла скорость возрастает от звуковой до сверхзвуковой величины.
Весовой расход воздуха через любое сечение выходного сопла имеет одну и ту же величину:
Это — уравнение неразрывности для потока сжимаемою газа. Отсюда может быть найдено соотношение между любыми двумя сечениями сопла.
Давление газа по мере приближения к выходу из сопла падает, как показано на рис. 269; при уменьшении давления (за критическую величину) скорость истечения растет медленнее, чем уменьшается плотность; поэтому увеличение скорости должно обеспечиваться расширением сопла: выходное сечение больше критического, Следует обратить внимание на различие между течением несжимаемой жидкости и течением газа при сверхкритическом перепаде давления: скорость несжимаемой жидкости (как и скорость газа при докритическом давлении) увеличивается в сужающихся трубах; наоборот, скорость при сверхкритических перепадах давления после перехода за звуковую величину увеличивается в расширяющихся соплах
Расширяющиеся сопла применяются в паровых и газовых турбинах, в реактивных двигателях и некоторых других устройствах
Рис. 269. Изменение давления и скорости в расширяющемся сопле для сверхзвуково течения воздуха.
При больших относительных перепадах давления понижение тем пературы газа, текущего по расширяющемуся соплу, бывает очень значительным. Так, например, когда то температура вытекающей струи воздуха понижается почти на 80°.
Течение со сжатием характеризуется уменьшением скорости потока и возрастанием давления, плотности и температуры газа Согласно уравнению (4) убыль кинетическои энергии вызывает прирос: теплосодержания и повышение температуры:
Отсюда относительное повышение теплосодержания при адиабатном течении со сжатием до полного затормаживания потока получается равным
Здесь величина пропорциональна квадрату скорости звука. [Действительно, по формуле (2) (стр 265) с другой стороны, следовательно,
Итак, относительное повышение теплосодержания зависит только от отношения начальной скорости газа к скорости звука в потоке до торможения газа.
Отношение скорости течения к скорости звука (от которого зависит изменение параметров газа при сжатии) называют числом Маха, или числом Берстоу, и обозначают символом М:
Вводя это обозначение в предыдущее уравнение, получаем
Когда изменения теплосодержания не слишком велики, так что теплоемкость можно считать постоянной, то
Все, что было сказано выше для течения с расширением, вследствие обратимости течения можно применить и к течению со сжатием, переменив только знаки скоростей (т. е. считая, например, для рис. 269, что течение происходит справа налево). Когда начальная скорость превосходит скорость звука, в сужающейся части сопла происходит торможение сверхзвукового потока В самом узком — критическом — сечении сопла скорость потока снижается до местной скорости звука, до величины скорости звука при той температуре, которая имеется в данном сечении (а температура в критическом сечении для течения со сжатием, понятно, больше начальной температуры). В расширяющемся участке сопла происходит дальнейшее торможение потока, при котором скорость понижается от звуковой до той или иной величины, иногда близкой к нулю, в зависимости от длины и геометрической формы сопла.
При больших начальных скоростях повышение температуры и увеличение давления при торможении намного превосходит те, которые имеют место при работе компрессоров. Так, для полета в стратосфере при давление при равновесном торможении повышается более чем в 150 раз, т. е. гораздо значительнее, чем в двигателе внутреннего сгорания. При давление при торможении повышается более чем в 5000 раз, а температура становится выше, чем внутри мартеновской печи. Боевые головки баллистических ракет для защиты от чрезмерного нагрева покрывают жаростойкими составами, которые при движении падающей ракеты в нижних слоях атмосферы частично оплавляются.
Когда газ затормаживается до полной остановки то по уравнению (12) при равновесном торможении получаются следующие значения для повышения температуры и давления:
Источник
