Газ наполняющий герметичный сосуд

5.4. Практическое применение уравнения состояния идеального газа

5.4.2. Уравнение состояния для газа в закрытом сосуде

При рассмотрении идеального газа, находящегося в закрытом сосуде (баллоне), необходимо учитывать, что изменение термодинамических параметров происходит при постоянной массе газа.

Для идеального газа, находящегося в закрытом сосуде, необходимо учитывать следующее:

• масса газа, находящегося в закрытом сосуде, вследствие изменения его термодинамических параметров не изменяется:

m = const;

• объем газа, заполняющего сосуд определенного объема, также фиксирован: V = const;
• постоянными также остаются следующие параметры газа:

ρ = const; ν = const; n = const;

где ρ — плотность газа; ν — количество вещества (газа); n — концентрация молекул (атомов) газа.

Для идеального газа, находящегося в закрытом сосуде и изменяющего свое состояние, уравнение Менделеева — Клапейрона записывается в виде системы (рис. 5.8):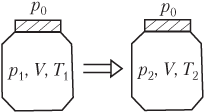Рис. 5.8

p1V=νRT1,p2V=νRT2,}

где p
1, T
1 — давление и температура газа в начальном состоянии; p
2, T
2 — давление и температура газа в конечном состоянии; V — объем баллона; ν — количество газа; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).

Термин избыточное давление, встречающийся в задачах об идеальном газе в закрытом сосуде (баллоне), означает абсолютную разность между давлением газа, находящегося в сосуде, и давлением на стенки сосуда снаружи:

p
изб = |p − p
0|,

где p — давление газа, находящегося внутри сосуда; p
0 — давление (атмосферное либо гидростатическое) на стенки сосуда снаружи.

Пример 13. Баллон рассчитан на максимальное избыточное давление 150 МПа. В него накачали газ при температуре 300 К до давления 120 МПа. Постепенно нагревая газ, баллон погружают в воду плотностью 1000 кг/м3 на глубину 1000 м. До какой максимальной температуры можно нагреть газ в баллоне, чтобы он не взорвался?

Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в баллоне:

• в начале нагревания

p
1V = νRT
1;

• в конце нагревания

p
2V = νRT
2;

где p
1 — первоначальное давление газа в баллоне; p
2 — давление газа в баллоне в конце нагревания; V — объем газа (баллона), V = const; ν — количество вещества (газа) в баллоне; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в начале процесса; T
2 — температура газа в конце процесса.

Отношение уравнений

p1Vp2V=νRT1νRT2

позволяет определить давление газа в конце процесса:

p2=p1T2T1.

В условии задачи задано максимальное избыточное давление, определяемое формулой

pизбmax=|p2−p0|,

где p
0 — давление снаружи баллона; p
2 — давление газа внутри баллона.

При погружении баллона в воду с одновременным нагреванием указанные давления снаружи и внутри баллона определяются следующими формулами:

• снаружи (сумма атмосферного и гидростатического давлений) —

p
0 = p
атм + p
гидр = p
атм + ρ0gh,

где p
атм — атмосферное давление; p
гидр — гидростатическое давление, p
гидр = ρ0gh; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — глубина погружения баллона;

• внутри (давление газа) —

p2=p1T2T1,

где T
2 — максимальная температура газа (искомая величина).

Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает

pизбmax=|p1T2T1−ρ0gh−pатм|≈|p1T2T1−ρ0gh|,

так как p
атм << ρ0gh, p
атм << p
2.

Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:

pизбmax=p1T2T1−ρ0gh, pизбmax=ρ0gh−p1T2T1,

из которых следуют две формулы для расчета искомой величины:

T2=T1⋅ρ0gh+pизбmaxp1, T2=T1⋅ρ0gh−pизбmaxp1.

Максимальному значению искомой температуры соответствует значение, рассчитанное по первой формуле:

T2=300⋅1000⋅10⋅1000+150⋅106120⋅106=400 К.

Чтобы баллон не взорвался, его можно погрузить на заданную глубину, одновременно нагревая до температуры 400 К.

Пример 14. Бутылка емкостью 0,75 л выдерживает максимальное избыточное давление 150 кПа. Из бутылки откачивают воздух и запечатывают некоторое количество твердого углекислого газа с молярной массой 44,0 г/моль. Атмосферное давление равно 100 кПа. Считая, что объем твердого углекислого газа пренебрежимо мал по сравнению с объемом бутылки, найти его максимальную массу, которая не вызовет взрыва бутылки при температуре 300 К?

Решение. Запишем уравнение Менделеева — Клапейрона для углекислого газа, находящегося в бутылке, после его превращения в газообразное состояние:

pV=mMRT,

где p — давление углекислого газа в бутылке; V — объем газа (бутылки); m — масса углекислого газа в бутылке; M — молярная масса углекислого газа; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа.

Записанное уравнение позволяет получить выражение для расчета давления газа внутри бутылки:

p=mRTVM.

В условии задачи задано максимальное избыточное давление, определяемое формулой

pизбmax=|p−p0|,

где p
0 — давление снаружи бутылки.

Указанные давления снаружи и внутри бутылки определяются следующим образом:

• снаружи (атмосферное давление) — p
  0;
• внутри (давление углекислого газа) —

p=mRTVM,

где m соответствует искомой величине — максимальной массе углекислого газа.

Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает

pизбmax=|mRTVM−p0|.

Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:

pизбmax=mRTVM−p0, pизбmax=p0−mRTVM,

из которых следуют две формулы для расчета искомой величины:

m=VM(p0+pизбmax)RT, m=VM(p0−pизбmax)RT.

Максимальному значению искомой массы соответствует значение, рассчитанное по первой формуле:

m=0,75⋅10−3⋅44,0⋅10−3(100+150)⋅1038,31⋅300=3,3⋅10−3 кг=3,3 г.

Чтобы бутылка не взорвалась, в нее можно запечатать не более 3,3 г твердого углекислого газа.

Пример 15. В наличии имеется неограниченное количество баллонов объемом по 4,0 л, заполненных некоторым идеальным газом до давления 500 кПа. Баллоны предназначены для наполнения газом оболочки аэрозонда и их можно соединять между собой. Сколько баллонов с газом необходимо одновременно подсоединить к пустой оболочке аэрозонда объемом 800 дм3, чтобы наполнить ее до давления 100 кПа, равного атмосферному? Температура газа при заполнении оболочки не изменяется.

Решение. Для осуществления процесса, описанного в условии задачи, требуется определенное количество газа ν.

Необходимое количество газа заполняет следующий объем:

• в начале процесса (до заполнения оболочки)

V
1 = NV
бал,

где N — количество баллонов; V
бал — объем одного баллона, V
бал = 4,0 л;

• в конце процесса (после заполнения оболочки)

V
2 = NV
бал + V
обол,

где V
обол — объем оболочки, V
обол = 800 дм3.

Указанное количество газа находится при давлении:

• в начале процесса (до заполнения оболочки) —

p
1 = 500 кПа

и совпадает с давлением газа в каждом из баллонов;

• в конце процесса (после заполнения оболочки) —

p
2 = 100 кПа

и совпадает с давлением в оболочке.

Считая процесс заполнения газом оболочки аэрозонда изотермическим, запишем уравнение Менделеева — Клапейрона следующим образом:

• в начале процесса (до заполнения оболочки) —

p
1V
1 = νRT,

где ν — количество вещества (газа) в оболочке; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);

• в конце процесса (после заполнения оболочки) —

p
2V
2 = νRT.

Равенство

p
1V
1 = p
2V
2,

записанное в явном виде

p
1NV
бал = p
2(NV
бал + V
обол),

позволяет получить формулу для вычисления искомого числа баллонов:

N=VоболVбал⋅p2p1−p2.

Произведем расчет:

N=800⋅10−34,0⋅10−3⋅100⋅103(500−100)⋅103=50.

Следовательно, для заполнения оболочки до указанного давления необходимо 50 баллонов с газом.

Пример 16. Аэростат, оболочка которого заполнена азотом с молярной массой 28 г/моль, находится в воздухе. Молярная масса воздуха равна 29 г/моль. Массы гондолы и оболочки аэростата пренебрежимо малы. Во сколько раз возрастет подъемная сила аэростата, если азот в его оболочке заменить на водород с молярной массой 2,0 г/моль, не изменяя при этом объем аэростата?

Решение. Силы (сила тяжести mg→ и сила Архимеда F→A), действующие на аэростат, показаны на рисунке.

Подъемная сила — это векторная сумма силы тяжести и силы Архимеда:

F→под=F→A+mg→,

где F→A — сила Архимеда, действующая на оболочку со стороны воздуха; mg→ — сила тяжести; m — масса газа, заполняющего оболочку аэростата; g→ — ускорение свободного падения.

В проекциях на вертикальную ось подъемная сила определяется следующими выражениями:

• при заполнении оболочки азотом —

F
под1 = F
A1 − m
1g,

где F
A1 — модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки азотом, F
A1 = ρ0gV
1; ρ0 — плотность воздуха; V
1 — объем оболочки аэростата при заполнении ее азотом (объем воздуха, вытесненного оболочкой); m
1 — масса азота, заполняющего оболочку, m
1 = ρ1V
1; ρ1 — плотность азота;

• при заполнении оболочки водородом —

F
под2 = F
A2 − m
2g,

где F
A2 — модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки водородом, F
A2 = ρ0gV
2; V
2 — объем оболочки аэростата при заполнении ее водородом (объем воздуха, вытесненного оболочкой); m
2 — масса водорода, заполняющего оболочку, m
2 = ρ2V
2; ρ2 — плотность водорода.

Искомой величиной является отношение

Fпод2Fпод1=FA2−m2gFA1−m1g.

С учетом записанных выражений для сил Архимеда, масс азота и водорода, а также равенства объемов оболочки при заполнении ее азотом и водородом (V
1 = V
2), указанное отношение принимает вид

Fпод2Fпод1=ρ0gV2−ρ2V2gρ0gV1−ρ1V1g=(ρ0−ρ2)V2g(ρ0−ρ1)V1g=ρ0−ρ2ρ0−ρ1.

Плотности воздуха, азота и водорода определим как отношения:

• для воздуха

ρ0=M0Vμ0,

где M
0 — молярная масса воздуха; V
µ0 — молярный объем воздуха;

• для азота

ρ1=M1Vμ1,

где M
1 — молярная масса азота; V
µ1 — молярный объем азота;

• для водорода

ρ2=M2Vμ2,

где M
2 — молярная масса водорода; V
µ2 — молярный объем водорода.

Молярные объемы (объемы одного моля) воздуха, азота и водорода равны между собой, так как газы находятся при одних и тех же условиях:

V
µ0 = V
µ1 = V
µ2 = V
µ.

Поэтому формула для расчета искомого отношения приобретает вид

Fпод2Fпод1=ρ0−ρ2ρ0−ρ1=M0−M2M0−M1.

Расчет дает значение:

Fпод2Fпод1=29⋅10−3−2,0⋅10−329⋅10−3−28⋅10−3=27.

При замене азота на водород в оболочке аэростата его подъемная сила возрастет в 27 раз.

Пример 17. Воздушный шар с температурой 300 К находится в воздухе при атмосферном давлении 100 кПа. Молярная масса воздуха составляет 29,0 г/моль. Объем воздушного шара равен 830 дм3, а масса его оболочки равна 333 г. На сколько градусов необходимо нагреть газ в оболочке, чтобы шар взлетел? Воздух в оболочке шара сообщается с атмосферой.

Решение. Силы, действующие на воздушный шар, показаны на рисунке:

• сила Архимеда

F
A = ρ0gV,

где ρ0 — плотность воздуха, окружающего шар; g — модуль ускорения свободного падения; V — объем оболочки шара (объем вытесненного оболочкой воздуха);

• сила тяжести

mg = (m
обол + m
возд)g,

где m
обол — масса оболочки; m
возд — масса воздуха в оболочке, m
возд = ρV; ρ — плотность воздуха внутри оболочки.

Шар взлетает, когда выполняется равенство

F→A+mg→=0,

или, в проекции на вертикальную ось, —

F
A − mg = 0.

Преобразуем равенство (условие равновесия шара в воздухе)

F
A = mg

с учетом записанных выше выражений

ρ0gV = (m
обол + m
возд)g, или (ρ0 − ρ)V = m
обол.

Входящие в равенство плотности воздуха не известны, но фигурируют в качестве параметра в уравнении состояния:

• для воздуха снаружи оболочки воздушного шара

p0=ρ0RT1M,

где p
0 — атмосферное давление; ρ0 — плотность воздуха снаружи оболочки; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура окружающего шар воздуха; M — молярная масса воздуха;

• для воздуха внутри оболочки воздушного шара

p=ρRT2M,

где p — давление воздуха внутри оболочки; ρ — плотность воздуха внутри оболочки; T
2 — температура воздуха внутри оболочки.

Давления воздуха внутри и снаружи оболочки воздушного шара одинаковы, так как воздух, находящийся в оболочке, сообщается с атмосферой; поэтому

p = p
0.

Плотности:

• для воздуха снаружи оболочки воздушного шара

ρ0=p0MRT1;

• для воздуха внутри оболочки воздушного шара

ρ=p0MRT2.

Подставим выражения для плотностей в условие равновесия шара в воздухе:

(1T1−1T2)p0MVR=mобол.

Температура воздуха внутри оболочки, при которой шар начинает взлетать, определяется как

T2=p0MVT1p0MV−RT1mобол,

а искомая разность —

ΔT=T2−T1=p0MVT1p0MV−RT1mобол−T1=T1p0MVRT1mобол−1.

Произведем вычисление:

ΔT=300100⋅103⋅29,0⋅10−3⋅830⋅10−38,31⋅300⋅333⋅10−3−1=158 К.

Следовательно, чтобы воздушный шар начал взлетать, воздух в его оболочке необходимо нагреть на 158 К, или 158 °С.

Пример 18. Камеру футбольного мяча объемом 3,00 л накачивают с помощью насоса, забирающего из атмосферы 0,150 л воздуха при каждом качании. Атмосферное давление составляет 100 кПа. Определить давление в камере после 30 качаний, если первоначально она была пустой. Температура постоянна.

Решение. За N качаний насос забирает из атмосферы определенное количество воздуха ν. Это же количество воздуха попадает в камеру футбольного мяча.

Указанное количество воздуха имеет следующий объем:

• воздух, забранный из атмосферы за N качаний насоса, —

V
1 = NV
нас,

где V
нас — объем насоса, V
нас = 0,150 л; N — количество качаний;

• воздух, накачанный в камеру футбольного мяча, —

V
2 = V
мяч,

где V
мяч — объем камеры мяча, V
мяч = 3,00 л.

Данное количество воздуха находится при следующем давлении:

• воздух, забранный из атмосферы за N качаний насоса, —

p
1 = 100 кПа

совпадает с атмосферным давлением;

• воздух, накачанный в камеру футбольного мяча, — p
  2 (является искомой величиной).

Считая процесс заполнения воздухом камеры мяча изотермическим, запишем уравнение Менделеева — Клапейрона следующим образом:

• для воздуха, забранного из атмосферы за N качаний насоса, —

p
1V
1 = νRT,

где R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);

• для воздуха, накачанного в камеру футбольного мяча, —

p
2V
2 = νRT.

Равенство

p
1V
1 = p
2V
2,

записанное в явном виде

p
1NV
нас = p
2V
мяч,

позволяет получить формулу для вычисления давления в камере футбольного мяча:

p2=p1NVнасVмяч.

Произведем вычисление:

p2=100⋅103⋅30⋅0,15⋅10−33,00⋅10−3=150⋅103 Па=150 кПа.