Газовый термометр состоит из двух одинаковых сосудов

^
Модель идеального газа

Основной особенностью газов является их малая плотность, благодаря чему среднее расстояние между молекулами оказывается во много раз больше размеров молекул. Поскольку радиус межмолекулярного взаимодействия также имеет порядок размера молекул, то, вследствие этого, взаимодействие между молекулами оказывается очень слабым, и при рассмотрении многих свойств газов им можно вообще пренебречь. Модель газа, в которой пренебрегают взаимодействием между молекулами, носит название идеального газа.

Уравнение состояния идеального газа

Идеальный газ подчиняется, как известно, уравнению состояния

PV=NkT (1)

где P, V, T – давление, объем, температура газа, N – число молекул газа в объеме V, k=1,38?10 23 Дж/К – постоянная Больцмана.

Умножив и поделив правую часть этого уравнения на массу молекулы, приведём его к другой форме:

(2)

где

R =k?NA= 8,314 Дж/моль?К – универсальная газовая постоянная,

? – масса моля этого газа, m – масса газа, заключенного в объеме V.

Уравнение (2) носит название уравнения Клапейрона – Менделеева.

Для постоянной массы газа, как видно из (1) или (2), если:

T=const, то PV=const – закон Бойля – Мариотта,
P=const, то V/T=const – закон Гей – Люссака,
V=const,то P/T=const – закон Шарля.

Семейства графиков этих законов изображены на рисунке.

Закон Бойля – Мариотта

Закон Гей – Люссака

Закон Шарля

Рис. 1

Для смеси газов справедлив закон Дальтона, гласящий, что давление смеси газов равно сумме парциальных давлений компонентов смеси. Иными словами, каждая компонента смеси оказывает на стенки сосуда такое давление, как если бы в сосуде находилась одна эта компонента.

Задача 1

Сколько молекул воздуха содержится в 1см3 при нормальных условиях?

Решение

Согласно уравнению состояния идеального газа P=nkT, откуда

Сравним эту величину с аналогичным числом для твёрдых или жидких тел (см. задачу 3 из предыдущего раздела). Как мы видели, в конденсированных телах (т.е. в жидких или твёрдых телах) эта величина имеет порядок 3?1022 см –3, т.е. в 1000 больше, чем в газе. Но это означает, что средние расстояния между молекулами в газах при обычных условиях приблизительно в 10 раз больше чем в конденсированных телах. В предыдущем разделе, обсуждая характер сил, действующих между молекулами, мы видели, что эти силы очень быстро убывают с увеличением расстояний между молекулами – как 1/ r –7. Таким образом, силы межмолекулярного взаимодействия в газах в миллионы раз слабее, нежели в конденсированных телах. Как видим, модель идеального газа при не слишком высоких плотностях газов работает очень хорошо.

Задача 2

Полагая, что воздух состоит на 80% из азота и на 20% из кислорода, найти парциальные давления азота и кислорода.

Решение

Выделим мысленно произвольный объём воздуха ^ . Пусть в этом объёме число молекул воздуха равно N. Обозначим число молекул азота и кислорода в этом объёме через N1 и N2. Тогда N= N1+ N2. Кроме того, для давления воздуха:

Как видим, парциальные давления азота и кислорода пропорциональны концентрации этих газов:

Отметим, что полученный ответ не зависит от температуры. Парциальные давления компонент смеси определяются только лишь концентрацией соответствующей компоненты.

Задача 3

В двух частях сосуда, объёмы которых V1 и ^ 2, находятся различные идеальные газы при одинаковой температуре Т. Число молекул в первой части сосуда – N1, во второй – N2. Каким будет давление в сосуде, если убрать перегородку, разделяющую сосуд?

Решение

Поскольку температура обоих газов одинакова, то никакого обмена энергией между молекулами этих газов происходить не будет. Следовательно, температура останется неизменной. Давление, согласно закону Дальтона найдём как сумму парциальных давлений газов, имея в виду, что каждый из газов заполняет теперь весь объём сосуда:

Задача 4

Давление воздуха внутри бутылки 105 Па при температуре +7оС. На сколько нужно нагреть бутылку, чтобы пробка вылетела? Без нагревания пробку можно вынуть, прикладывая к ней силу 10 Н. Площадь S поперечного сечения пробки 2 см2.

Решение

Очевидно, давление внутри бутылки нужно увеличить на столько, чтобы сила избыточного давления ^ на пробку стала равной 10 Н:

F=?P?S.

Давление воздуха при постоянном объёме растёт пропорционально температуре:

Откуда найдём ?Т:

При записи ответа мы использовали тот факт, что изменение температуры по абсолютной шкале температур и шкале Цельсия одинаково.

Задача 5

За сколько ходов поршня насоса с рабочим объёмом ^ можно повысить давление с Р0 до Р1 в сосуде с объёмомV0? Нагревом газа пренебречь.

Решение

Процесс накачки изотермический. Этот процесс можно представить как изотермическое сжатие газа от объёма V0 + nV и давления Р0 до объёма V0 давления Р1:

P0(V0 + nV) = P1V0.

Откуда найдём n:

Задача 6

За сколько ходов поршня N насоса с рабочим объёмом ^ можно откачать сосуд объёмом V0 снизив в нём давление с Р0 до Р1? Процесс откачки происходит при постоянной температуре.

Решение

Пусть на п-м ходе поршня давление снизилось с Рп до Рп +1. Процесс откачки изотермический, поэтому:

РпV = Рп +1(V0 + V).

Записав эти уравнения для всех ходов поршня с первого по N-й, и перемножив их, получим:

РVN = Р1(V0 + V)N.

Откуда найдём:

Задача 7

На два длинных цилиндрических мешка радиусом r и длины ^ , сделанных из нерастяжимого материала и заполненных газом положили тяжёлую плиту массы М, в результате чего они расплющились до толщины h. Внешнее давление Р0. Каким было начальное давление в мешках, если температура в них не изменялась?

Решение

Поскольку мешки нерастяжимы, то периметр мешков не изменился (см. Рис. 1):

2?r=2(h+l),

здесь l – ширина мешка.

Рис. 1
Поскольку h, то l=?r. Тем самым, первоначальный объём мешка V1 = ?r2L, а объём сплющенного мешка V2= l? h? L = ?r?h?L.

На каждый из мешков приходится половина веса плиты, который уравновешивается силой избыточного давления газа в мешке:

Отсюда найдём ^ :

Поскольку процесс сжатия газа был изотермическим, то:

P1V1 = P2V2,

или

P1?r2L = PlhL.

Здесь Р1 – начальное давление в мешке.

Отсюда найдём начальное давление:

Задача 8

Газовый термометр состоит из двух одинаковых сосудов с газом объема ^ 0каждый, соединенных трубкой длины L и сечения S. Трубку перекрывает капля ртути. Если температуры газов в объемах одинаковы, ртуть находится посередине трубки. Правый объем помещают в термостат с температурой Т, Проградуируйте термометр, найдя зависимость температуры газа в левом объеме от смещения х ртути из положения равновесия.

Рис. 1

Решение

Поскольку трубка горизонтальна, то давления по обе стороны от капли ртути будут одинаковы. Кроме того, массы газов по обе стороны от капли остаются неизменными.

Запишем уравнение состояния газа в каждой из частей сосуда:

P (V0 + Sl/2+Sx) =NkT, P (V0 + Sl/2–Sx) =NkT0.

Поделив первое уравнение на второе, найдём:

Если V0>>Sl, то полученная формула упрощается:

И для относительного изменения температуры ?Т = Т – Т0:

Задача 9

Каким станет давление в закрытом сосуде с водой, если силы взаимодействия между молекулами внезапно исчезнут?

Решение

Отсутствие взаимодействия между молекулами вещества означает, что это вещество является идеальным газом. Поэтому:

Здесь ? = 103 кг/м – плотность воды, температуру приняли равной 300 К (27оС).

Если Вам понравился наш сайт, Вы можеть разместить кнопку на своём сайте или блоге:

Источник

Задача 1

Для изменения собственного объема сыпучего материала его помещают в цилиндр, который герметически закрывают поршнем. Затем измеряют давление воздуха при одной и той же температуре и двух положениях поршня, когда суммарный объем воздуха и материала равен . Каков объем материала по этим данным?

Ответ:

Задача 2

На два длинных цилиндрических мешка радиуса r и длины , сделанных из нерастяжимого материала и заполненных газом, положили плиту массы m, в результате чего они сплющились до толщины . Внешнее давление . Определите начальное давление в мешках, если температура газа в них не изменялась.

Газовый термометр состоит из двух одинаковых сосудов Ответ:

Задача 3

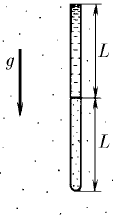
Нижний конец вертикальной узкой трубки 2 L запаян, а верхний открыт в атмосферу. В нижней половине трубки находится газ при температуре , а верхняя ее половина заполнена ртутью. До какой минимальной температуры надо нагреть газ в трубке, чтобы он вытеснил всю ртуть? Внешнее давление в миллиметрах ртутного столба равно L.

Ответ:

Задача 4

За сколько ходов поршневого насоса с рабочим объемом V можно понизить давление в сосуде вместимости с атмосферного до P?

Ответ:

Задача 5

Газовый термометр состоит из двух одинаковых сосудов вместимости каждый, соединенных трубкой длины l и сечения S. Трубку перекрывает капля ртути. Сосуды наполнены газом. Если температура газа в обоих сосудах одинакова, ртуть находится посередине трубки. Один сосуд помещен в термостат с температурой . Проградируйте термометр, найдя зависимость температуры газа во втором сосуде от смещения ртути из положения равновесия.

Ответ:

Газовый термометр состоит из двух одинаковых сосудов Задача 6

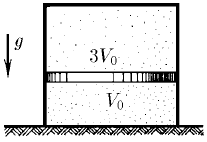
В цилиндрическом сосуде с газом находится в равновесии тяжелый поршень. Масса газа и его температура над поршнем и под ним одинакова. Отношение внутреннего объема верхней части сосуда к внутреннему объему нижней части равно 3. Каким будет это соотношение, если температуру газа увеличить в два раза?

Ответ:

Задача 7

На поверхности жидкости плотности ρ плавает цилиндрический тонкостенный стакан, наполовину погруженный в жидкость. На сколько погрузится стакан в жидкость, если его поставить на поверхность жидкости вверх дном? Высота стакана h, давление воздуха .

Ответ:

Задача 8

В прямоугольном сосуде с непроницаемыми стенками находится слева тяжелая жидкость, отделенная подвижным тонким поршнем от воздуха в правой части сосуда. В начальный момент поршень находится в равновесии и делит объем сосуда пополам. На сколько смещается поршень вправо, если температура системы уменьшится в три раза? Тепловым расширением жидкости и стенок сосуда пренебречь. Трения нет. Длина сосуда 2 a.

Ответ:

Задача 9

Воздух внутри оболочки воздушного шара вместимости V нагревается газовой горелкой до температуры T, превышающей температуру окружающего воздуха. Какова при атмосферном давлении грузоподъемность этого воздушного шара? Молярная масса воздуха µ.

Ответ:

Задача 10

Два мыльных пузыря радиуса сливаются в один. Найдите поверхностное натяжение мыльной воды, если радиус образовавшегося пузыря равен r, а атмосферное давление равно .

Ответ:

Дата: 2018-12-28, просмотров: 254.

Источник

Похожие работы

Основы молекулярно-кинетической теории – страница №2/24

Свойства идеальных газов

Модель идеального газа

Уравнение состояния идеального газа

Идеальный газ подчиняется, как известно, уравнению состояния

PV=NkT (1)

где P, V, T – давление, объем, температура газа, N – число молекул газа в объеме V, k=1,3810 23 Дж/К – постоянная Больцмана.

Умножив и поделив правую часть этого уравнения на массу молекулы, приведём его к другой форме:

(2)

где

R =kNA= 8,314 Дж/мольК – универсальная газовая постоянная,

 – масса моля этого газа,m – масса газа, заключенного в объеме V.

Уравнение (2) носит название уравнения Клапейрона – Менделеева.

Для постоянной массы газа, как видно из (1) или (2), если:

T=const, то PV=const – закон Бойля – Мариотта,
P=const, то V/T=const – закон Гей – Люссака,
V=const,то P/T=const – закон Шарля.

Семейства графиков этих законов изображены на рисунке.

Закон Бойля – МариоттаЗакон Гей – ЛюссакаЗакон ШарляРис. 1

Для смеси газов справедлив законДальтона, гласящий, что давление смеси газов равно сумме парциальных давлений компонентов смеси. Иными словами, каждая компонента смеси оказывает на стенки сосуда такое давление, как если бы в сосуде находилась одна эта компонента.

Задача 1

Сколько молекул воздуха содержится в 1см3 при нормальных условиях?

Решение

Согласно уравнению состояния идеального газа P=nkT, откуда

Сравним эту величину с аналогичным числом для твёрдых или жидких тел (см. задачу 3 из предыдущего раздела). Как мы видели, в конденсированных телах (т.е. в жидких или твёрдых телах) эта величина имеет порядок 31022 см –3, т.е. в 1000 больше, чем в газе. Но это означает, что средние расстояния между молекулами в газах при обычных условиях приблизительно в 10 раз больше чем в конденсированных телах. В предыдущем разделе, обсуждая характер сил, действующих между молекулами, мы видели, что эти силы очень быстро убывают с увеличением расстояний между молекулами – как 1/ r –7. Таким образом, силы межмолекулярного взаимодействия в газах в миллионы раз слабее, нежели в конденсированных телах. Как видим, модель идеального газа при не слишком высоких плотностях газов работает очень хорошо.

Задача 2

Полагая, что воздух состоит на 80% из азота и на 20% из кислорода, найти парциальные давления азота и кислорода.

Решение

Выделим мысленно произвольный объём воздуха V. Пусть в этом объёме число молекул воздуха равно N.Обозначим число молекул азота и кислорода в этом объёме через N1и N2. Тогда N= N1+N2. Кроме того, для давления воздуха:

Как видим, парциальные давления азота и кислорода пропорциональны концентрации этих газов:

Задача 3

В двух частях сосуда, объёмы которых V1 и V2, находятся различные идеальные газы при одинаковой температуре Т. Число молекул в первой части сосуда – N1, во второй – N2. Каким будет давление в сосуде, если убрать перегородку, разделяющую сосуд?

Решение

Задача 4

Давление воздуха внутри бутылки 105 Па при температуре +7оС. На сколько нужно нагреть бутылку, чтобы пробка вылетела? Без нагревания пробку можно вынуть, прикладывая к ней силу 10 Н. Площадь Sпоперечного сечения пробки 2 см2.

Решение

Очевидно, давление внутри бутылки нужно увеличить на столько, чтобы сила избыточного давления Fна пробку стала равной 10 Н:

F=PS.

Давление воздуха при постоянном объёме растёт пропорционально температуре:

Откуда найдём Т:

Задача 5

За сколько ходов поршня насоса с рабочим объёмом V можно повысить давление с Р0 доР1 в сосуде с объёмомV0? Нагревом газа пренебречь.

Решение

P0(V0 + nV) = P1V0.

Откуда найдём n:

Задача 6

За сколько ходов поршня N насоса с рабочим объёмом V можно откачать сосуд объёмом V0 снизив в нём давление с Р0 доР1? Процесс откачки происходит при постоянной температуре.

Решение

Пусть на п–м ходе поршня давление снизилось с Рпдо Рп +1. Процесс откачки изотермический, поэтому:

РпV = Рп +1(V0 + V).

Записав эти уравнения для всех ходов поршня с первого по N–й, и перемножив их, получим:

РVN = Р1(V0 + V)N.

Откуда найдём:

Задача 7

На два длинных цилиндрических мешка радиусом rи длины L>>r, сделанных из нерастяжимого материала и заполненных газом положили тяжёлую плиту массы М, в результате чего они расплющились до толщины hr. Внешнее давление Р0. Каким было начальное давление в мешках, если температура в них не изменялась?

Решение

Поскольку мешки нерастяжимы, то периметр мешков не изменился (см. Рис. 1):

2r=2(h+l),

здесь l – ширина мешка.

Рис. 1

Поскольку hr, то l=r. Тем самым, первоначальный объём мешка V1 = r2L, а объём сплющенного мешка V2= l h L = rhL.

Отсюда найдём Р:

Поскольку процесс сжатия газа был изотермическим, то:

P1V1 = P2V2,

или

P1r2L = PlhL.

Здесь Р1 – начальное давление в мешке.

Отсюда найдём начальное давление:

Задача 8

Газовый термометр состоит из двуходинаковых сосудов с газом объема V0каждый, соединенных трубкой длины L и сечения S. Трубку перекрывает капля ртути. Если температуры газов в объемах одинаковы, ртуть находится посередине трубки. Правый объем помещают в термостат с температурой Т, Проградуируйте термометр, найдя зависимость температуры газа в левом объеме от смещения хртути из положения равновесия.

Рис. 1

Решение

Запишем уравнение состояния газа в каждой из частей сосуда:

P (V0 + Sl/2+Sx) =NkT, P (V0 + Sl/2–Sx) =NkT0.

Поделив первое уравнение на второе, найдём:

Если V0>>Sl, то полученная формула упрощается:

И для относительного изменения температуры Т = Т–Т0:

Задача 9

Решение

Здесь  = 103 кг/м – плотность воды, температуру приняли равной 300 К (27оС).

следующая страница >>

Источник

Тема. Решение задач по теме«Основное уравнение молекулярно-кинетической теории газов. Газовые законы».

Цели:

– углубить знание основ молекулярно-кинетической теории вещества на примере наиболее простого состояния – газообразного;

– убедиться в правильности основных положений молекулярно-кинетической теории газов.

Ход занятия

В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности.

Прежде чем приступить к выполнению задания, рекомендуется изучить теорию по теме занятия, используя предоставленные учащимся материалы, а также рекомендованные учебники и учебные пособия.

Качественные вопросы

1. Какие величины характеризуют состояние макроскопических тел в тепловом равновесии?

2. Каковы отличительные признаки состояния теплового равновесия?

3. Чем отличается газ от жидкостей и твердых тел с точки зрения молекулярно-кинетической теории строения вещества?

4. Чем отличается реальный газ от идеального?

5. Какова связь между средней кинетической энергией поступательного движения молекул газа и его равновесной температурой ?

6. Стенки сосуда, в котором находится газ с температурой Т, имеют температуру . В каком случае давление газа на стенки сосуда больше:

а) когда стенки сосуда холоднее газа

или б) когда теплее ?

Имейте в виду, что если температуры Тст и Т совпадают, молекула, ударяясь о стенку, меняет нормальную компоненту импульса на (рис. 1).

7. На рис. 2 изображены изотермы для одной и той же массы идеального газа, соответствующие трем температурам: . Как соотносятся между собой эти температуры?

8. На рис. 3 изображены три изохоры для одной и той же массы идеального газа, соответствующие трем значениям объема . Как соотносятся между собой эти объемы?

9. Сжимается или разрежается газ в процессе, изображенном на рис. 4?

10. Изобразите в координатах Р, Т замкнутый цикл, представленный на рис. 5.

11. Нагревается или охлаждается идеальный газ, если он расширяется по закону , где a и n – постоянные, причем ?

12. Зависит ли подъемная сила аэростата от температуры окружающего воздуха?

13. Почему электрические лампочки накаливания заполняются инертным газом при давлении, существенно меньшем атмосферного?

14. Произведение давления газа на его объем (PV) не меняется с изменением объема при постоянной температуре, только если предположить, что газы, с которыми мы имеем дело, являются идеальными.

Определите, будет ли уменьшаться или увеличиваться произведение РV при очень сильном сжатии газа, если не делать предположения об идеальности последнего.

Примеры решения расчетных задач

Задача 1. Пробирка массой М содержит моль идеального газа массой m при температуре Т. Пробирку открывают, вынимая из нее пробку пренебрежимо малой массы. Оцените скорость пробирки после того, как весь газ выйдет из нее наружу. Считать, что дело происходит в вакууме.

Решение:

Направим ось х вдоль оси пробирки. Половина общего числа молекул газа имеют проекцию скорости . Эти молекулы уйдут из пробирки, не передав ей никакого импульса. Другая половина молекул передаст задней стенке пробирки свой двойной импульс, а затем также покинет пробирку. Следовательно, пробирка получит импульс (в проекции на ось х):

где – проекция скорости пробирки, – масса молекулы газа, – среднее значение модуля проекции ее скорости и – число Авогадро.

Учитывая, что для равновесного состояния , то есть средний квадрат проекции скорости на любую ось равен среднего квадрата самой скорости, и что (k – постоянная Больцмана), получим, считая

отсюда

где R – универсальная газовая постоянная.

Ответ: .

Задача 2. Дан воздушный шар с постоянным объемом V = 1,10 м3. Масса оболочки (объемом оболочки пренебречь) составляет кг. Шар должен стартовать при окружающей температуре воздуха °С и нормальном атмосферном давлении Па. Плотность воздуха при этих условиях имеет значение кг/м3. Вычислите температуру , которую должен иметь нагретый воздух внутри шара, чтобы он мог свободно парить в воздухе.

Решение:

Условие равновесия шара в воздухе запишем в виде

где – архимедова сила, равная ,

а – сила тяжести шара с воздухом:

откуда

. (1)

Из уравнения газового состояния

следует, что

, .

Отсюда

. (2)

Из выражений (1) и (2) получаем:

. (3)

Подстановка числовых данных приводит к результату: К, или С.

Ответ: С.

Задача 3. В сосуде находится углекислый газ. При некоторой температуре 25 % молекул углекислого газа диссоциировали на атомарный кислород и окись углерода. Во сколько раз давление в сосуде при этих условиях будет больше того давления, которое было бы при отсутствии диссоциации?

Решение:

Используем закон Дальтона для смеси нескольких газов, химически не реагирующих между собой и находящихся в состоянии теплового равновесия при температуре Т. Давление смеси газов равно сумме парциальных давлений компонентов смеси:

Воспользуемся основным уравнением молекулярно-кинетической теории:

Смесь газов занимает объем V. Тогда

Пусть в сосуде объемом V было N молекул СО2. Диссоциировало молекул СО2 и образовалось N/4 молекул О и N/4 молекул СО. При этом осталось молекул СО2. Общее число молекул в сосуде после диссоциации

До диссоциации было давление

После диссоциации давление в смеси газов стало

Таким образом, давление после диссоциации больше в

(раз).

Ответ: в 1,25 раз.

Задача 4. Два одинаковых баллона соединены трубкой с клапаном, пропускающим газ из одного баллона в другой при разности давлений ΔР ≥ 1,10 атм. Сначала в одном баллоне был вакуум, а в другом – идеальный газ при температуре 27 °С и давлении Р1 = 1,00 атм. Затем оба баллона нагрели до температуры t2 = 107 °C. Найдите давление газа в баллоне, где был вакуум.

Решение:

Введем следующие обозначения: Р1 – первоначальное давление газа в первом баллоне; Р2 – давление в первом баллоне после открытия клапана и перетекания части газа во второй баллон; Р3 – давление во втором баллоне, где раньше был вакуум.

Запишем уравнение состояния для газа в первом и втором баллонах.

– (4)

начальное состояние газа в первом баллоне.

– (5)

конечное состояние газа в первом баллоне.

– (6)

состояние газа во втором баллоне, где был вакуум.

Поступление газа из первого баллона во второй будет иметь место до тех пор, пока давление Р2 на ΔР превышает давление Р3. Это означает, что

. (7)

Воспользовавшись (4) и сложив равенства (2) и (3), получаем:

. (8)

Очевидно, что

(9)

находим из (1).

. (10)

Подставляя в (8) выражение (9) и принимая во внимание (10), получаем:

. (11)

Решая (11) относительно Р3, находим:

Подстановка численных значений приводит к результату:

Р3 = 10 кПа = 0,1 атм.

Ответ: 0,1 атм.

Задача 5. Из баллона со сжатым кислородом объемом 100 л из-за неисправности крана вытекает газ. При температуре 273 К манометр на баллоне показывал давление 2·106 Па. Через некоторое время при температуре 300 К манометр показал то же давление. Сколько газа вытекло из баллона?

Решение:

В системе СИ (системе интернациональной)

л = 0,1 м–3,

Па,

Т1 = 273 К,

Т2 = 300 К.

= ?

Запишем уравнение Менделеева–Клапейрона для двух состояний газа:

Из (12) и (13) ,

или

Из (12)

Тогда

кг.

Ответ: Δm = 0,254 кг.

Задача 6. Плотность газа ρ, состоящего из смеси гелия и аргона, при давлении 152 кН/м2 и температуре 300 К равна 2 кг/м3. Сколько атомов гелия содержится в 1 см3 газовой смеси? Молярные массы гелия и аргона равны соответственно 4·10–3 и
4·10–2 кг/моль.

Решение:

Для смеси газов:

. (14)

По определению ρ имеем:

. (15)

Равенства (14) и (15) – два уравнения с двумя неизвестными – и . Решим эти уравнения совместно.

м3.

Итак,

Решаем эту систему уравнений и находим . Из первого уравнения выражаем через :

Это выражение подставляем во второе уравнение:

;

Ответ: .

Задача 7. В вертикальном закрытом с обоих концов цилиндре находится легкоподвижный поршень, по обе стороны которого по одному молю воздуха. В равновесном состоянии при температуре 300 К объем верхней части цилиндра в h = 4 раза больше объема нижней части. При какой температуре отношение этих объемов станет (рис. 6)?

Решение:

Обозначим параметры состояния моля идеального газа при двух равновесных положениях поршня соответственно

I – T1, P1, V1; ;

II – T1, P2, V2; .

На основании уравнения состояния моля идеального газа в принятых обозначениях имеем:

, (16)

, (17)

, (18)

. (19)

Учтем, что при любом положении поршня суммарный объем, занимаемый газом, остается постоянным, поэтому можно записать:

. (20)

Выразив V1, V2, V ‘1 и V ‘2 из уравнений (16)–(19) и подставив полученные значения в (20), находим:

. (21)

Решив (21) относительно Т ‘, получаем:

. (22)

Установим далее связь между Р1 и Р2 и и . В равновесном положении поршня давление газа в части II цилиндра равно сумме давлений в части I и давления, обусловленного весом поршня, поэтому можно записать:

, (23)

где Q – вес поршня, S – площадь его поперечного сечения.

Из уравнений (16) и (17) с учетом данных условия находим:

. (24)

Подставляя (24) в (23), получаем:

. (25)

С учетом (24) для Р2 находим:

. (26)

Выполнив полностью аналогичное рассмотрение для второго равновесного положения поршня (при соотношении объемов ), получим равенства:

, (27)

. (28)

Подставляя (25)–(28) в (22), получаем:

. (29)

Подставляя в (29) численные значения, находим:

= 420 К.

Ответ: 420 К.

Задача 8. С какой максимальной силой прижимается к телу человека медицинская банка, если диаметр ее отверстия d = 4 см? В момент прикладывания к телу воздух в ней имеет температуру t1 = 80 °C, температура окружающего воздуха t0 = 20 °C, атмосферное давление = 105 Па. Изменением объема воздуха в банке при ее присасывании к телу пренебречь.

Решение:

При остывании воздуха в банке давление в ней становится меньше атмосферного, и сила, с которой она прижимается к телу, равна

где , – давление в банке после остывания воздуха.

Изменением объема в банке пренебрегаем, тогда по закону Шарля

при .

Тогда .

Решаем, применяя систему единиц СИ:

Ответ: .

Задача 9. Некоторая масса азота совершает замкнутый процесс, изображенный на рис. 7 в координатах V, T. Минимальное давление азота в этом процессе Па. Определите массу газа и его давление в точке 1 (рис. 7).

Решение:

По закону Клапейрона для данной массы газа. Тогда Р минимально, если максимально. Обратим внимание, что прямые, проходящие через данную точку и начало координат – изобары, а .

tg α

;

Па (в СИ).

Из уравнения Менделеева–Клапейрона:

; кг (в CИ).

1 л = 10–3 м–3.

Ответ: m = 55 г; Р1 = 4?105 Па.

Задачи для самостоятельной работы

1. Современные вакуумные насосы позволяют понижать давление до 1,3·10–10 Па (10–12 мм рт. ст.). Сколько молекул газа содержится в 1 см3 при указанном давлении и температуре 27 °С?

Ответ: 3,14·104 см–3.

2. Где больше молекул: в комнате объемом 50 м3 при нормальном атмосферном давлении и температуре 20 °С или в стакане воды объемом 200 см3?

Ответ: в комнате.

3. Определите плотность азота при давлении 106 Па, если среднеквадратичная скорость молекул равна 5·103 м/с.

Ответ: 0,12 кг/м3.

4. Чему равна средняя кинетическая энергия поступательного движения молекулы азота, если давление газа 5·105 Па, а его плотность 4 кг/м3?

Ответ: 8,72·10–21 Дж.

5. Средняя кинетическая энергия молекул одноатомного газа равна 3,2·10–19 Дж. Давление газа равно атмосферному. Найдите число молекул газа в 1 л.

Ответ: 4,68·1020.

6. Чему равна средняя энергия поступательного движения молекул кислорода, если его масса равна 1 кг, объем 1 м3, а давление 2·105 Па?

Ответ: 1,59·10–20 Дж.

7. Молекулярный пучок азота ударяется о неподвижную стенку. После соударения молекулы абсолютно упруго отражаются от стенки. Определите давление пучка на стенку, если скорост?