Где больше давление в сосуде
Все, что необходимо знать о силе давления воды
Пловец, нырнувший глубоко, ощущает боль в ушах. На барабанные перепонки воздействует сила давления воды.
Корабль в воде не тонет благодаря выталкивающей силе. Вода способна легко изменять свою форму, она воздействует на поверхности тел при соприкосновении с ними.
Чему равна сила давления воды и что это такое, расскажем в статье.
Что это такое?
В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.
Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.
Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.
Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.
Факторы, влияющие на показатель
При отсутствии внешнего воздействия, играют роль два фактора:
Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.
Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:
При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.
На дно и стенку сосуда – в чем разница?
Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.
Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.
Единицы измерения
Давление воды измеряют в:
- паскалях – Па;
- метрах водяного столба – м. в. ст.
- атмосферах – атм.
Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).
Формулы расчета
Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).
Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.
Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.
Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.
Расчет давления воды на дно и стенки сосуда в видео:
Применение на практике
Примеры использования знаний свойств воды:
- Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
- Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
- Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
- Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.
Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:
- выжимка масла из семян растений;
- спуск на воду со стапелей построенного судна;
- ковка и штамповка деталей;
- домкраты для подъема грузов.
Заключение
Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.
Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.
Источник
Давление жидкости на дно и стенки сосуда. Формула гидростатического давления
Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.
Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).
Расчет давления жидкости на дно сосуда
Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.
Давление, которое жидкость создает на дно сосуда, называется гидростатическим. «Гидро» — это «вода», а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.
Давление в толще жидкости
Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.
Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.
Давление в наклонном сосуде
Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.
Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.
А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1 28 марта, 2019
Источник
Давление в жидкости и газе. Расчет давления жидкости на дно и стенки сосуда
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
405. Поднимающиеся со дна водоема пузырьки воздуха увеличиваются в объеме по мере приближения к поверхности. Почему?
С приближением к поверхности, давление воды на пузырек падает.
406. Воду из узкого высокого стакана перелили в широкую кастрюлю. Как изменилось давление воды на дно?
Давление уменьшилось, поскольку уменьшилась высота водяного столба.
407. На рисунке 44 изображен старинный опыт: в крышку бочки, наполненную доверху водой, была вставлена высокая узкая трубка. Когда в трубку налили воды, бочка разорвалась. Объясните, почему небольшое количество воды, которую пришлось налить в трубку, могло разорвать бочку?
Давление на стенки бочки будет зависеть от плотности жидкости и высоты водяного столба и не зависит от площади поперечного сечения сосуда.
408. В сосуд налили слой воды высотой 15 см. каково давление этого слоя на дно сосуда?
409. Чему равно давление воды на глубине 50 см?
410. Банка высотой 50 см наполнена водою. Определите давление на 1 см2 дна банки.
411. В мензурку, площадь дна которой 20 см2 , налита вода до высоты 10 см. сколько граммов воды налито? Чему равно давление воды на дно мензурки?
412. Высота уровня воды в водопроводе 10 м (рис.45). Одинаковы ли давления на стенки трубы на различных высотах? Каково давление воды у нижнего конца трубы?
413. Каково давление на дверцу в шлюзовых воротах на глубине 12 м (рис. 46)?
414. В стакан высотой 10 см налита доверху ртуть. Вычислить давление на дно стакана.
415. Вычислите давление столбика ртути высотой 76 см.
416. Поршневой насос может произвести давление 5·105 Па. На какую высоту можно поднять воду этим насосом?
417. В трех сосудах налита вода до одной и той же высоты (рис. 47). В каком сосуде налито больше воды? В каком сосуде больше давление на дно?
Давление во всех сосудах на дно одинаково.
418. Внутрь жидкости погружен брусок (рис 48). Одинаковые ли давления испытывают боковые стенки бруска (левая и правая, передняя и задняя)? Одинаковые ли давления испытывают верхняя и нижняя грани бруска?
Боковые стенки испытывают одинаковое давление; верхняя и нижняя – разное.
419. Рассмотрите рисунок 48. Высота погруженного бруска АК=5 см. На сколько больше давление на грани MNKL, чем на ABCD, если брусок помещен в воду на глубину 12 см (до нижней грани)?
420. Если в подводной части судна появилась пробоина, то на эту пробоину накладывают «пластырь» — кусок паруса, который давлением воды прижимается к корпусу судна и не пропускает в пробоину воду. Определите силу, с которой прижимается пластырь, если площадь пробоины 0,5 м2 , а глубина, на которой сделана пробоина , 2 м.
421. В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают Расплавленный металл (рис. 49). Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке 49 слева изображена изложница, справа — подъем изложницы с отлитого слитка.
Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7,2 г/см3.
422. Для спуска водолаза на очень большую глубину применяется специальный металлический скафандр (рис . 50). Какую силу давления должен выдержать этот скафандр на глубине 300 м, если общая поверхность скафандра составляет 2,5 м2 ?
423. Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое специальной пробкой из огнеупорного металла. Определите давление расплавленной стали на пробку, если высота налитого металла 2 м, а плотность расплавленной стали 7,3 г/см³.
424. Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?
425. Определите давление воды на стенки котла водяного отопления, если высота труб 20 м?
426.Вычислите разность давлений в трубах водопровода на нижнем этаже здания и на этаже, расположенном выше на 15 м?
427. Батискаф спустился в море на глубину в 50 м. Каково давление на поверхность батискафа на данной глубине?
428. Давление в водопроводе 4·105 Па. С какой силой давит вода на пробку, закрывающую отверстие трубы, если площадь отверстия 4 см2 ?
429. Давление в трубах водопровода 4·105 Па. На какую высоту будет бить вода из пожарной трубы, присоединенной к этому водопроводу, если не принимать во внимание сопротивление воздуха и трение воды в трубах?
430. Человек стоит на кожаном мешке с водой (рис. 51). Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающаяся с мешком поверхности платформы 1000 см2.
Источник
Источник
Давление крови в различных участках сосудистой системы. Теоретические основы кровообращения
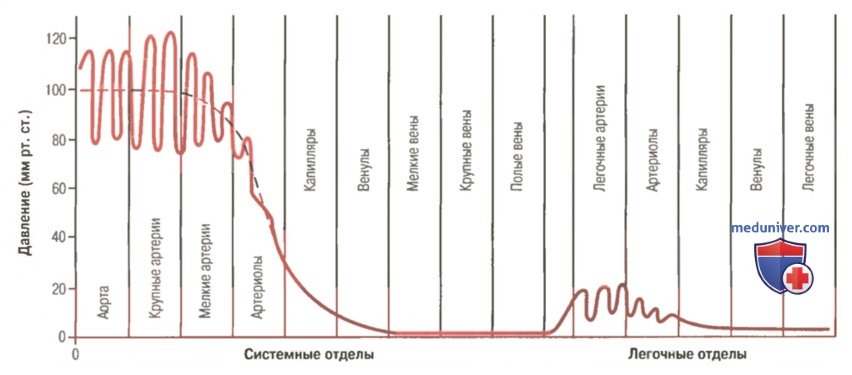
Среднее давление в аорте поддерживается на высоком уровне (примерно 100 мм рт. ст.), поскольку сердце непрестанно перекачивает кровь в аорту. С другой стороны, артериальное давление меняется от систолического уровня 120 мм рт. ст. до диастолического уровня 80 мм рт. ст., поскольку сердце перекачивает кровь в аорту периодически, только во время систолы.
По мере продвижения крови в большом круге кровообращения среднее давление неуклонно снижается, и в месте впадения полых вен в правое предсердие оно составляет 0 мм рт. ст.
Давление в капиллярах большого круга кровообращения снижается от 35 мм рт. ст. в артериальном конце капилляра до 10 мм рт. ст. в венозном конце капилляра. В среднем «функциональное» давление в большинстве капиллярных сетей составляет 17 мм рт. ст. Этого давления достаточно для перехода небольшого количества плазмы через мелкие поры в капиллярной стенке, в то время как питательные вещества легко диффундируют через эти поры к клеткам близлежащих тканей.
В правой части рисунке показано изменение давления в различных участках малого (легочного) круга кровообращения. В легочных артериях видны пульсовые изменения давления, как и в аорте, однако уровень давления значительно ниже: систолическое давление в легочной артерии — в среднем 25 мм рт. ст., а диастоли-ческое — 8 мм рт. ст. Таким образом, среднее давление в легочной артерии составляет всего 16 мм рт. ст., а среднее давление в легочных капиллярах равно примерно 7 мм рт. ст. В то же время общий объем крови, проходящий через легкие за минуту, — такой же, как и в большом круге кровообращения. Низкое давление в системе легочных капилляров необходимо для выполнения газообменной функции легких.

Давление крови в различных отделах сосудистой системы у человека, находящегося в горизонтальном положении
Теоретические основы кровообращения
Несмотря на то, что объяснение многих механизмов кровообращения довольно сложное и неоднозначное, можно выделить три основных принципа, которые определяют все функции системы кровообращения.
1. Объемный кровоток в органах и тканях почти всегда регулируется в зависимости от метаболических потребностей тканей. Когда клетки активно функционируют, они нуждаются в усиленном снабжении питательными веществами и, следовательно, в усиленном кровоснабжении — иногда в 20-30 раз большем, чем в состоянии покоя. Однако сердечный выброс не может увеличиться более чем в 4-7 раз. Значит, невозможно просто увеличить кровоток в организме, чтобы удовлетворить потребность какой-либо ткани в усиленном кровоснабжении. Вместо этого сосуды микроциркуляторного русла в каждом органе и ткани немедленно реагируют на любое изменение уровня метаболизма, а именно: на потребление тканями кислорода и питательных веществ, накопление углекислого газа и других метаболитов.
Все эти сдвиги непосредственно влияют на мелкие сосуды, вызывая их расширение или сужение, и таким образом контролируют местный кровоток в зависимости от уровня метаболизма.
2. Сердечный выброс контролируется главным образом суммой всех местных тканевых кровотоков. Из капиллярных сетей периферических органов и тканей кровь по венам сразу возвращается к сердцу. Сердце автоматически реагирует на возросший приток крови, начиная немедленно перекачивать больше крови в артерии. Таким образом, работа сердца зависит от потребностей тканей в кровоснабжении. Этому способствуют и специфические нервные сигналы, поступающие к сердцу и регулирующие его насосную функцию рефлекторно. 3. В целом системное артериальное давление контролируется независимо от регуляции местного тканевого кровотока и сердечного выброса.
В сердечно-сосудистой системе существуют эффективные механизмы регуляции артериального давления. Например, каждый раз, когда давление оказывается ниже нормального уровня (100 мм рт. ст.), в течение секунд рефлекторные механизмы вызывают изменения деятельности сердца и состояния сосудов, направленные на возвращение артериального давления к нормальному уровню. Нервные сигналы способствуют: (а) увеличению силы сердечных сокращений; (б) сужению венозных сосудов и перемещению крови из емкого венозного русла к сердцу; (в) сужению артериол в большинстве периферических органов и тканей, что затрудняет отток крови из крупных артерий и поддерживает в них высокий уровень давления.
Кроме того, в течение более длительного периода времени (от нескольких часов до нескольких дней) окажет влияние важная функция почек, связанная с секрецией гормонов, контролирующих артериальное давление, и с регуляцией объема циркулирующей крови. Итак, потребности отдельных органов и тканей в кровоснабжении обеспечиваются разными механизмами, регулирующими деятельность сердца и состояние сосудов. Далее в статьях на сайте мы подробно проанализируем основные механизмы регуляции местного кровотока, сердечного выброса и артериального давления.
– Также рекомендуем “Регуляция объема кровотока и периферического сопротивления. Объемный кровоток”
Оглавление темы “Сосудистая система”:
1. Электрокардиограмма при фибрилляции желудочков. Электрошоковая дефибрилляция желудочков
2. Ручной массаж сердца в помощь дефибрилляции. Фибрилляция предсердий
3. Трепетание предсердий. Остановка сердца
4. Функциональные участки системы кровообращения. Объемы крови в различных отделах сосудистой системы
5. Давление крови в различных участках сосудистой системы. Теоретические основы кровообращения
6. Регуляция объема кровотока и периферического сопротивления. Объемный кровоток
7. Ультразвуковой флоуметр. Ламинарное течение крови в сосудах
8. Турбулентное течение крови. Давление крови
9. Сопротивляемость сосудов. Проводимость сосудов
10. Закон Пуазейля. Диаметр артериол и их сопротивление
Источник
