Гидравлический поршень сообщающиеся сосуды
Определение
Соединенные между собой сосуды называют сообщающимися.
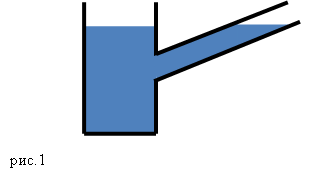
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.

Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
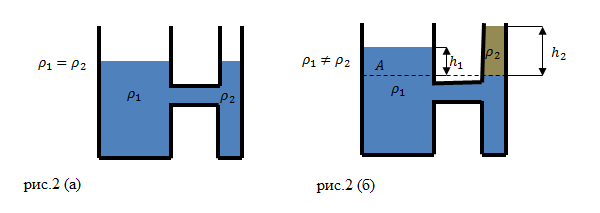
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
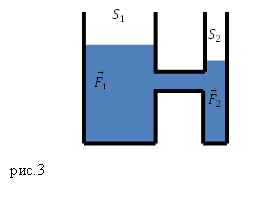
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
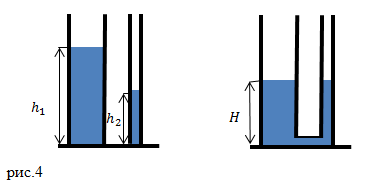
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
Формула давления жидкости отличается от формулы, с помощью которой можно рассчитать давление твердого тела. Потому, что давление жидкости не зависит от площади поверхности, на которую жидкость давит.
Закон Паскаля
Французский физик, Блез Паскаль, в 1653 году сформулировал закон: «Давление, которое мы оказываем на жидкость (или газ), она без изменения передаст в любую точку и во всех направлениях».
Мы немного упростим формулировку:
Жидкость (или газ) передает давление, оказанное на нее, одинаково и без изменений во все стороны.
Это значит, что на одной и той же глубине жидкость будет одинаково давить и на дно, и на стенки сосуда.
Рис. 1. Чем глубже, тем больше давление жидкости, но в любой точке жидкость передает это давление одинаково во все стороны
На рисунке 1 изображен сосуд, наполненный жидкостью. Высоту столбика жидкости – то есть, глубину, отсчитываем от поверхности жидкости.
Видно, что на разных глубинах давление отличается.
[ large begin{cases} h_{1} < h_{2} < h_{3} \ P_{1} < P_{2} < P_{3} end{cases} ]
Чем глубже, тем больше давление жидкости. Но в любой точке оно одинаково передается во все стороны.
Формула давления жидкости
Формула, по которой можно посчитать давление жидкости:
[ large boxed{ P = rho_{text{ж}} cdot g cdot h }]
( P left(text{Па}right) ) – давление жидкости;
( displaystyle rho_{text{ж}} left(frac{text{кг}}{text{м}^3} right) ) – плотность жидкости;
( displaystyle g left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения;
Для большинства школьных задач можно принимать ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) );
( h left(text{м}right) ) – высота столбика жидкости.
В формулу для давления жидкости не входит площадь S поверхности, на которую эта жидкость давит.
Поэтому, давление жидкости не зависит от площади. А давление твердого тела рассчитывают по другой формуле.
В некоторых задачах указывают объем используемой жидкости. И иногда просят рассчитать силу давления. Чтобы получить правильный ответ для таких задач, нужно уметь переводить площади и объемы в единицы системы СИ.
Сообщающиеся сосуды
Сообщающиеся сосуды – это емкости, расположенные на плоской горизонтальной поверхности, у дна они соединяются трубками.
Если в один из сосудов начать наливать жидкость, то она будет распределяться по всем сосудам, так, что ее уровень будет одинаковым во всех сосудах (рис. 2).
Рис. 2. В сообщающихся сосудах уровень жидкости будет одинаковым
Неважно, какую форму имеет сосуд. Давление жидкости во всех сосудах будет одинаковым. Поэтому одинаковой будет высота h столбика жидкости во всех сосудах.
U-образное колено
U-образное колено – это два сообщающихся сосуда, диаметры сосудов одинаковые.
Жидкости, которые заливают в колено, не должны смешиваться (рис. 3). Например, можно залить в оду трубку воду, а в другую — масло.
Рис. 3. Два сообщающихся сосуда одинакового диаметра образуют U-образное колено
Запишем формулы для расчета давления в левом (P_{1}) и правом (P_{2}) частях колена.
[ large boxed{begin{cases} P_{1} = rho_{1} cdot g cdot h_{1} \ P_{2} = rho_{2} cdot g cdot h_{2} end{cases}} ]
Чем больше разница плотностей двух жидкостей, тем больше отличаются высоты их столбиков.
При решении задач общую нижнюю часть колена не учитываем. На рисунке 3 она отделена от верхней части горизонтальной линией.
Давление столбиков, оставшихся в верхней части, будет одинаковым.
( P_{1} ) – давление жидкости в левой части колена;
( P_{2} ) – давление жидкости в правой части колена.
[ large begin{cases} P_{1} = P_{2} \ rho_{1} cdot g cdot h_{1} = rho_{2} cdot g cdot h_{2} end{cases} ]
Обе части последнего уравнения разделим на ускорение свободно падения. Тогда получим соотношение для высот столбиков жидкости и их плотностей:
[ large boxed{ rho_{1} cdot h_{1} = rho_{2} cdot h_{2} }]
Высоты столбиков можно измерить линейкой. Зная плотность одной из жидкостей, можно найти плотность второй жидкости.
Примечание: Давление жидкостей часто измеряют в миллиметрах ртутного столба или метрах водяного столба. Переходите по ссылке, чтобы узнать, как связаны эти единицы измерения и как давление переводить в систему СИ.
Гидравлический пресс
Молекулы жидкости плотно упакованы, они прилегают друг к другу. Поэтому жидкости не сжимаемы! Это свойство жидкостей используют в гидравлическом прессе.
Гидравлический пресс – это два сообщающихся сосуда. Их называют цилиндрами. Диаметры цилиндров отличаются. Внутри каждого цилиндра вверх и вниз может свободно перемещаться поршень (рис. 4). Поршень плотно прилегает к стенкам цилиндра, чтобы жидкость из цилиндра не просачивалась наружу.
Рис. 4. Гидравлический пресс – это два сообщающихся сосуда различных диаметров, по сосудам могут без трения перемещаться поршни
Перемещаясь, поршень из цилиндра вытесняет жидкость в соседний цилиндр. Объем жидкости, вытесненной из одного цилиндра, совпадает с объемом, перешедшим в другой цилиндр, так как жидкость не проливается наружу.
[ large Delta V_{1} = Delta V_{2} ]
( Delta V_{1} left(text{м}^{3}right) ) – объем жидкости, вытесненной из первого цилиндра;
( Delta V_{2} left(text{м}^{3}right) ) – объем жидкости, перешедшей во второй цилиндр.
Из геометрии известно, объем цилиндрической фигуры можно найти по формуле:
[ large boxed{ Delta V = Delta h cdot S }]
( Delta h left(text{м}right) ) – высота столбика вытесненной жидкости;
( S left(text{м}^{2}right) ) – площадь поршня (или основания цилиндра);
Так как объемы вытесненной и перешедшей в другой цилиндр жидкостей равны, можем записать
[ large Delta h_{1} cdot S_{1} = Delta h_{2} cdot S_{2} ]
То есть, высоты столбиков отличаются во столько же раз, во сколько отличаются площади поршней.
Площадь поверхности поршня и его диаметр связаны соотношением:
[ large boxed{ S_{text{круга}} = pi cdot frac{d^{2}}{4} }]
( S left(text{м}^{2}right) ) – площадь поршня;
( d left(text{м}right) ) – диаметр поршня;
Давления в цилиндрах будут равны.
[ large P_{text{общ.лев}} = P_{text{общ.прав}} ]
Поршни в цилиндрах не двигаются – т. е. находятся в равновесии. Запишем условия равновесия для поршней:
[ large boxed{ frac{F_{1}}{S_{1}} + rho_{1} cdot g cdot h_{1} = frac{F_{2}}{S_{2}} + rho_{2} cdot g cdot h_{2} } ]
Здесь дробью вида (displaystylelarge frac{F}{S}) обозначено давление твердого тела (ссылка) — поршня.
Назовем цилиндр большого диаметра большим цилиндром, а цилиндр малого диаметра – малым. Сформулируем принцип действия гидравлического пресса:
С помощью малой силы в малом цилиндре мы можем создавать большую силу в большом цилиндре.
Источник
Давление
Действие силы на твердое тело зависит не только от модуля этой силы, но и от площади поверхности тела, на которую она действует. Взаимодействие жидкостей и газов с твердыми телами, а также взаимодействие между соседними слоями жидкости или газа тоже происходит не в отдельных точках, а на определенной поверхности их соприкосновения. Поэтому для характеристики подобных взаимодействий введено понятие давления.
Давлением р называют величину, равную отношению модуля силы давления F, действующей перпендикулярно поверхности, к площади 5 этой поверхности:
p=F/S. (5.1)
При равномерном распределении сил давления давление на всех участках поверхности одинаково и численно равно силе давления, действующей на поверхность единичной площади.
Единицу давления устанавливают из формулы (5.1). В СИ за единицу давления принято давление, вызываемое силой 1 Н, равномерно распределенной по перпендикулярной к ней поверхности площадью 1 м2. Эту единицу давления называют паскаль (Па): 1 Па=1 Н/м2.
Часто используют и следующие внесистемные единицы давления:
- техническая атмосфера (ат): 1 ат=9,8·104 Па;
- физическая атмосфера (атм), равная давлению, производимому столбом ртути высотой 760 мм. Как показано в § 24, 1 атм = 1,033 ат = 1,013·105 Па;
- миллиметр ртутного столба (мм рт. ст.): 1 мм рт. ст. » 133,3 Па;
- бар (в метеорологии используют миллибар); 1 бар=105 Па, 1 мбар=102 Па.
Закон Паскаля для жидкостей и газов
Твердые тела передают производимое на них извне давление по направлению действия силы, вызывающей это давление. Совсем иначе передают внешнее давление жидкости и газы.
Рассмотрим следующий эксперимент (рис. 48). В сосуде, закрытом пробкой, находится вода. В пробку вставлены три одинаковые по диаметру трубки, нижние отверстия которых находятся в воде на одинаковой глубине, но направлены в разные стороны (вниз, вбок и вверх), а также не достающая до воды трубка, к которой подсоединен резиновый баллон от пульверизатора. Закачивая с его помощью воздух в сосуд, мы увеличиваем давление, оказываемое воздухом на поверхность воды в сосуде. Замечаем, что при этом во всех трех трубках вода поднимается до одной и той же высоты. Следовательно, неподвижная жидкость, находящаяся в замкнутом сосуде, передает производимое на нее внешнее давление по всем направлениям одинаково (т.е. без изменения).
Наблюдения показывают, что так же передают внешнее давление и газы, находящиеся в закрытом сосуде. Описанная закономерность была впервые обнаружена французским ученым Паскалем и получила название закона Паскаля.
Гидростатическое давление
На каждую молекулу жидкости, находящейся в поле тяготения Земли, действует сила тяжести. Под действием этих сил каждый слой жидкости давит на расположенные под ним слои. По закону Паскаля это давление передается жидкостью по всем направлениям одинаково. Следовательно, в жидкостях существует давление, обусловленное силой тяжести.
Наблюдения показывают, что жидкость, находящаяся в сосуде в состоянии покоя, давит на дно и стенки сосуда и на любое тело, погруженное в эту жидкость. Давление, оказываемое покоящейся жидкостью на любую соприкасающуюся с ней поверхность, называют гидростатическим.
Формула гидростатического давления
Гидростатическое давление можно определить с помощью прибора, называемого гидростатическими весами Паскаля (рис. 49). В подставке П, сквозь которую проходит кольцевой патрубок К, можно поочередно герметично закреплять сосуды С любой формы, не имеющие дна. Подвижным дном этих сосудов служит подвешенная на коромысле равноплечих весов плоская круглая площадка Д, расположенная вблизи нижнего отверстия патрубка К. Эта площадка прижимается к торцу патрубка силой, вызываемой тем, что на чашку весов, подвешенную на другом их коромысле, ставится гиря Г. К подставке П прикреплена линейка Л, по которой определяют высоту h жидкости в сосуде, закрепленном на подставке.
Опыт производят так. На под-ставке укрепляют сосуд, имеющий форму прямого кругового цилиндра. В него наливают воду до тех пор, пока вес этой воды не станет равным весу гири, поставленной на правую чашку весов, т.е. Рж=Рг. (Поддержание этого количества воды автоматически обеспечивается самим прибором, так как если вес воды в сосуде превысит вес гири, дно приоткроется и излишек воды вытечет.)
В цилиндрическом сосуде вес жидкости Pж=rжghS, где ж=rж – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости, S – площадь основания цилиндра, поэтому на дно сосуда жидкость оказывает давление
р=Pж/S=rжgh. (5.2)
Формула (5.2) определяет значение гидростатического давления.
Теоретический вывод формулы гидростатического давления
Выделим внутри покоящейся жидкости неподвижный элемент ее объема DV в виде прямого кругового цилиндра высотой h с основаниями, имеющими малую площадь DS, параллельными свободной поверхности жидкости (рис. 50). Верхнее основание цилиндра находится от поверхности жидкости на глубине h1, а нижнее – на глубине h2>h1.
На выделенный элемент объема жидкости действуют по вертикали три силы: силы давления F1=p1DS и F2=p2DS (где p1 и p2 – значения гидростатического давления на глубинах h1 и h2) и сила тяжести Fт=rgDV =rghDS.
Выделенный нами элемент объема жидкости покоится, значит, F1+F2+Fт=0, а следовательно, равна нулю и алгебраическая сумма проекций этих сил на вертикальную ось, т. е. p2DS-p1DS-rghDS=0, откуда получаем
p2-p1=rgh. (5.3)
Пусть теперь верхняя грань выделенного цилиндрического объема жидкости совпадает с поверхностью жидкости, т.е. h1=0. Тогда h2=h и p2=p, где h – глубина погружения, а р – гидростатическое давление на данной глубине. Считая, что на поверхности жидкости давление р1=0 (т.е. без учета внешнего давления на поверхность жидкости), из (5.3) получаем формулу для гидростатического давления р=rgh, которая совпадает с формулой (5.2).
Сообщающиеся сосуды
Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне.
Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Возьмем два цилиндрических сообщающихся сосуда одинакового диаметра (рис. 51), на их дно нальем слой ртути (заштрихован), а поверх него в цилиндры нальем жидкости с разными плотностями, например r2<r1 (слой ртути нужен для того, чтобы жидкости не смешивались). Мы увидим, что если эти жидкости находятся в состоянии покоя, их уровни h1 и h2 различны (h2>h1).
Мысленно выделим внутри трубки, соединяющей сообщающиеся сосуды и заполненнной ртутью, площадку площади S, перпендикулярную горизонтальной поверхности. Так как жидкости покоятся, давление на эту площадку слева и справа одинаково, т.e. p1=p2. Согласно формуле (5.2), гидростатическое давление p1=r1gh1 и p2=r2gh2. Приравняв эти выражения, получаем r1h12h2, откуда = r
h1/h2=r2/r1. (5.4)
Следовательно, разнородные жидкости в состоянии покоя устанавливаются в сообщающихся сосудах таким образом, что высоты их столбов оказываются обратно пропорциональными плотностям этих жидкостей.
Если r1=r2, то из формулы (5.4) следует, что h1=h2, т.е. однородные жидкости устанавливаются в сообщающихся сосудах на одинаковом уровне.
Принцип действия гидравлического пресса
Гидравлический пресс представляет собой два сообщающихся сосуда цилиндрической формы и разного диаметра, в которых имеются поршни, площади которых S1 и S2 различны (S2 >> S1). Цилиндры заполнены жидким маслом (обычно трансформаторным) . Схематически устройство гидравлического пресса изображено на рис. 52 (на этом рисунке не показаны резервуар с запасом масла и система клапанов).
Без нагрузки поршни находятся на одном уровне. На поршень S1 действуют силой F1, а между поршнем S2 и верхней опорой закладывают тело, которое нужно прессовать.
Сила F1, действуя на поршень S1, создает в жидкости дополнительное давление р=F1/S1. По закону Паскаля это давление передается жидкостью по всем направлениям без изменения. Следовательно, на поршень S2 действует сила давления
F2=pS2=F1S2/S1.
Из этого равенства следует, что
F2/F1=S2/S1. (5.5)
Следовательно, силы, действующие на поршни гидравлического пресса, пропорциональны площадям этих поршней. Поэтому с помощью гидравлического пресса можно получить выигрыш в силе тем больший, чем S2 больше S1.
Гидравлический пресс широко используется в технике.
Источник
Источник
