Глаз наблюдателя не видит дна сосуда
Условие задачи:
Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит заднюю вертикальную стенку. Сколько воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет, находящийся на расстоянии 10 см от задней стенки сосуда на его дне? Ребро сосуда 40 см.
Задача №10.3.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(l=10) см, (a=40) см, (V-?)
Решение задачи:
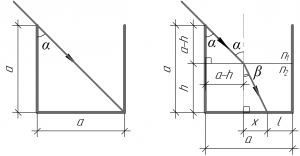Разумеется, сначала нужно сделать рисунки к задаче. Рассмотрим рисунок слева, он поможет нам найти угол падения луча (alpha). Так как сосуд имеет форму куба, то синус угла (alpha) можно найти следующим образом:
[sin alpha = frac{a}{{sqrt {{a^2} + {a^2}} }}]
[sin alpha = frac{{sqrt 2 }}{2};;;;(1)]
Теперь займемся правым рисунком. Из равенства (1) следует, что угол (alpha) равен 45°, и это очень важный вывод. Значит в прямоугольном треугольнике, образованном лучом, стенкой сосуда и поверхностью воды, оба катета равны (left( {a – h} right)) (смотрите рисунок справа).
Для ситуации на рисунке справа запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin alpha = {n_2}sin beta;;;;(2)]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления воды (n_2) равен 1,33.
Попытаемся найти синус угла (beta), для чего найдем противолежащий катет (x) в соответствующем прямоугольном треугольнике.
[x = a – l – left( {a – h} right)]
[x = h – l]
Сделаем важную оговорку: так как (x) не может быть меньше нуля, то ({h} > {l}), это пригодится нам в дальнейшем решении.
Тогда синус угла (beta) найдем по формуле (гипотенузу в том же прямоугольном треугольнике найдем по теореме Пифагора):
[sin beta = frac{{h – l}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }};;;;(3)]
Подставим в уравнение (2) выражения (1) и (3):
[frac{{sqrt 2 {n_1}}}{2} = frac{{{n_2}left( {h – l} right)}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }}]
Как Вы должны понимать, физика в этой задаче закончилась, осталась только математика – нужно решить данное уравнение. Перепишем его в следующем виде:
[frac{{sqrt 2 {n_1}}}{{2{n_2}}} = frac{{h – l}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }}]
Возведем в квадрат обе части этого уравнения:
[frac{{n_1^2}}{{2n_2^2}} = frac{{{{left( {h – l} right)}^2}}}{{{{left( {h – l} right)}^2} + {h^2}}}]
Перемножим “крест-накрест”:
[n_1^2{left( {h – l} right)^2} + n_1^2{h^2} = 2n_2^2{left( {h – l} right)^2}]
Раскроем скобки в обеих частях уравнения:
[n_1^2{h^2} – 2n_1^2hl + n_1^2{l^2} + n_1^2{h^2} = 2n_2^2{h^2} – 4n_2^2hl + 2n_2^2{l^2}]
Перенесем все в правую часть и сгруппируем:
[left( {2n_2^2 – 2n_1^2} right){h^2} – left( {4n_2^2 – 2n_1^2} right)hl + left( {2n_2^2 – n_1^2} right){l^2} = 0]
Поделим все на (l^2):
[left( {2n_2^2 – 2n_1^2} right){left( {frac{h}{l}} right)^2} – left( {4n_2^2 – 2n_1^2} right)left( {frac{h}{l}} right) + left( {2n_2^2 – n_1^2} right) = 0]
Решим данное квадратное уравнение относительно (frac{h}{l}), для чего перейдем к нахождению дискриминанта:
[D = {left( {4n_2^2 – 2n_1^2} right)^2} – 4left( {2n_2^2 – 2n_1^2} right)left( {2n_2^2 – n_1^2} right)]
Раскрываем скобки:
[D = 16n_2^4 – 16n_1^2n_2^2 + 4n_1^4 – 16n_2^4 + 8n_1^2n_2^2 + 16n_1^2n_2^2 – 8n_1^4]
[D = 8n_1^2n_2^2 – 4n_1^4]
[D = 4n_1^2left( {2n_2^2 – n_1^2} right)]
Учитывая численные значения показателей преломления, нетрудно сделать вывод, что дискриминант – положительный. Тогда корни уравнения следующие:
[frac{h}{l} = frac{{4n_2^2 – 2n_1^2 pm sqrt {4n_1^2left( {2n_2^2 – n_1^2} right)} }}{{2left( {2n_2^2 – 2n_1^2} right)}}]
[frac{h}{l} = frac{{4n_2^2 – 2n_1^2 pm 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}]
Посчитаем численное значение корней:
[left[ begin{gathered}
frac{h}{l} = frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} + 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}} = 2,686 hfill \
frac{h}{l} = frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} – 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}} = 0,614 hfill \
end{gathered} right.]
Как Вы видите, второй корень не удовлетворяют условию ({h} > {l}). Значит уровень воды (h) равен:
[h = left( {frac{{4n_2^2 – 2n_1^2 + 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}} right)l]
Искомый объем воды легко найти по формуле:
[V = {a^2}h]
Окончательно получим:
[V = left( {frac{{4n_2^2 – 2n_1^2 + 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}} right){a^2}l]
[V = left( {frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} + 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}}} right) cdot {0,4^2} cdot 0,1 = 0,043;м^3 = 43;л]
Ответ: 43 л.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Голландский механик, физик и математик, создатель волновой теории света. Первый иностранный член Лондонского королевского общества (с 1663). Учился в университетах Лейдена и
Бреды, где изучал юридические науки и математику. В 22 года он опубликовал работу об определении длины дуг окружности, эллипса и гиперболы. В 1654 г. появилась его работа «Об определении величины окружности», явившаяся важнейшим вкладом в теорию определе-
ния отношения окружности к диаметру. Затем последовали другие значительные математические трактаты по исследова- нию циклоиды, логарифмической и цеп- ной линии и др.
Его трактат «О расчетах при игре в кости» (1657) – одно из первых исследований в области теории вероят- ностей. Совместно с Р. Туком установил постоянные точки термометра – точку таяния льда и точку кипения воды. В эти же годы он работает над усовершенство- ванием объективов астрономических труб, стремясь увеличить их светосилу и устранить хроматическую аберрацию. С их помощью открыл в 1655 г. спутник планеты Сатурн (Титан), определил период его обращения и установил, что Сатурн окружен тонким кольцом, нигде к нему не прилегающим и наклонным к эклиптике. Все наблюдения приведены им в классической работе «Система Сатурна» (1659). В этой же работе он дал первое описание туманности в созвездии Ориона и сообщил о полосах на поверх- ностях Юпитера и Марса.
Астрономические наблюдения тре- бовали точного и удобного измерения времени. В 1657 г. он изобрел первые маятниковые часы, снабженные спуско- вым механизмом; свое изобретение опи- сал в работе «Маятниковые часы» (1658). Второе, расширенное издание этой рабо- ты вышло в 1673 г. в Париже. В ее первых 4 частях он исследовал ряд проблем, связанных с движением маятника. Он дал решение задачи о нахождении цен- тра качания физического маятника – пер- вой в истории механики задачи о движении системы связанных материаль- ных точек в заданном силовом поле. В этой же работе установил таутохронность движения по циклоиде и, разработав теорию эволют плоских кривых, доказал, что эволюта циклоиды есть также цик- лоида, но по-другому расположенная относительно осей. В 1665 г., при основании Французской АН, был пригла- шен в Париж в качестве ее председателя, где и прожил почти безвыездно 16 лет (1665-1681). В 1680 г. работал над созда- нием «планетной машины» – прообраза современного планетария – для конст- рукции которой разработал достаточно полную теорию цепных, или непрерыв- ных, дробей. Это – последняя работа, выполненная им в Париже.
В 1681 г., вернувшись на родину, он снова занялся оптическими работами. В 1681-1687 гг. он производил шлифовку объективов с огромными фокусными расстояниями в 37, 54 и 63 м. Тогда же сконструировал окуляр, носящий его имя, который применяется до сих пор. Весь цикл его оптических работ завершается знаменитым «Трактатом о свете» (1690). В нем впервые в совершенно отчетливой форме излагается и применяется к объяснению оптических явлений волно- вая теория света. В главе 5-й «Трактата о свете» дал объяснение явления двойного лучепреломления, открытого в кристал- лах исландского шпата; классическая теория преломления в оптически одно- осных кристаллах до сих пор излагается на основе этой главы. К «Трактату о свете» он добавил в виде приложения рассуждение «О причинах тяжести», в котором он близко подошел к открытию закона всемирного тяготения. В своем последнем трактате «Космотеорос» (1698), опубликованном посмертно, основывается на теории о множествен- ности миров и их обитаемости. В 1717 г. трактат был переведен на русский язык по приказанию Петра I. [1]
Механика
1657 Изобретение маятниковых часов. Совершенствованием часов, Гюйгенс занимался почти сорок лет.
1668 Х. Гюйгенс работает над теорией соударения тел
Астрономия
1655 Гюйгенс открывает Титан – самый большой спутник Сатурна, при помощи собственноручно построенного телескопа.
1672. Обнаружил ледяную маску на южном полюсе Марса.
Математика
1651 Христиан Гюйгенс опубликовал “Рассуждения о квадратуре гиперболы, эллипса и круга”.
1654. Открыл теорию эволют и эвольвент.
1657. Выходит трактат «О расчетах при игре в кости» — одна из первых работ по теории вероятностей.
Оптика
1678. Выходит «Трактат о свете» вошедший в историю, как первое научное сочинение по волновой оптике.[2]
Основные открытия
Христиан Гюйгенс опубликовал “Рассуждения о квадратуре гиперболы, эллипса и круга”.
1654
Открыл теорию эволют и эвольвент.
1655
Гюйгенс открывает Титан – самый большой спутник Сатурна, при помощи собственноручно построенного телескопа.
1657
Изобретение маятниковых часов. Совершенствованием часов, Гюйгенс занимался почти сорок лет.
1657
Выходит трактат «О расчетах при игре в кости» — одна из первых работ по теории вероятностей.
1668
Х. Гюйгенс работает над теорией соударения тел.
1672
Выходит трактат «О расчетах при игре в кости» — одна из первых работ по теории вероятностей.
1678
Выходит «Трактат о свете» вошедший в историю, как первое научное сочинение по волновой оптике.
Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис.1). Этот принцип в равной мере пригоден для описания распространения волн любой природы: механических, световых и т. д. Гюйгенс сформулировал его первоначально именно для световых волн.
Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.
Закон отражения
С помощью принципа Гюйгенса можно вывести закон, которому подчиняются волны при отражении от границы раздела сред.
Рассмотрим отражение плоской волны. Волна называется плоской, если поверхн- ости равной фазы (волновые поверхности) представляют собой плоскости. На (рис.2) MN – отражающая поверхность, прямые и — два луча падающей плоской волны (они параллельны друг другу). Плоскость AC – волновая поверхность этой волны.
Угол a между падающим лучом и перпендикуляром к отражающей поверхности и точке падения называют углом падения.
Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности AC достигают отражающей границы не одновременно. Возбуждение колебаний в точке Aначнется раньше, чем в точке B, на время
где — скорость волны.
В момент, когда волна достигнет точки B и в этой точке начнется возбуждение колебаний, вторичная волна с центром в точке A уже будет представлять собой полусферу радиусом . Радиусы вторичных волн от источников, расположенных между точками A и B, меняются так, как показано на (рис.2). Огибающей вторичных волн является плоскость DH, касательная к сферическим поверхностям. Она представляет собой волновую поверхность отраженной волны. Отраженные лучи и перпендикулярны волновой поверхности DB. Угол между перпендикуляром к отражающей поверхности и отраженным лучом называют углом отражения.
Так как AD=CB и треугольники ADB и ACB прямоугольные, то . Но и как углы с перпендикулярными сторонами. Следовательно, угол отражения равен углу падения:
(1)
Кроме того, как вытекает из построения Гюйгенса, падающий луч, луч отраженный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости. Эти два утверждения представляют собой закон отражения света.
Если обратить направление распространения световых лучей, то отраженный луч станет падающим, а падающий — отраженным. Обратимость хода световых лучей — их важное свойство.
Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент. Из принципа Гюйгенса выведен закон отражения волн.[3]
Условие задачи.
Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит стенку CD. До какой высоты h надо заполнить сосуд водой (), чтобы наблюдатель смог увидеть предмет F, находящийся на расстоя- нии b=10см от точки D?
Решение: Так как, согласно условию задачи, глаз не видит дна сосуда, а сосуд имеет форму куба, угол падения луча зрения на поверхность жидкости равен (рис. 3).
Из прямоугольного треугольника NKF видно, что
.
Отсюда
(2)
Согласно закону преломления
Тогда
; (3)
После подстановки (3) в (2) получим:
Ответ:
В каком году появилась работа Гюйгенса «Об определении величины окружности»?
ВЫБЕРИТЕ ЭЛЕМЕНТ
Кто изобрел маятниковые часы?
Где Гюйгенс обнаружил ледяную маску?
Кудрявцев П. С. Курс истории физики \ М.:Просвещение,1982.-448с.
Биография Христиана Гюйгенса mailto:\ https://persons-info.com/index.php?ptranslit=GIUIGENS_KHristian&p_tab=250&pid=7454&p_tab=246
Самин Д. К. Сто великих ученых \ М: «Вече», 2000
Биография Христиана Гюйгенса. (б.д.). Получено 13 сентябрь 2012 г., из https://persons-info.com/index.php?ptranslit=GIUIGENS_KHristian&p_tab=250&pid=7454&p_tab=246
Кудрявцев, П. (1982). Курс истории физики. Москва: Просвещение.
Самин, К. Д. (200). Сто великих ученых. Москва: Вече.
Источник
ГЕОМЕТРИЧЕСКАЯ
ОПТИКА
С о д е р ж а н и е к н и г и
1. в В
Е Д Е Н И Е.
2. Т Е О Р Е Т И Ч Е С К И Й О Б З О Р.
3. Р Е Ш Е Н И Е З А Д А Ч Ч А С Т
и
1
ЕГЭ
–
108 З А Д А Ч.
3-1. ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ
ОПТИКИ.
3-2. ПЛОСКИЕ ЗЕРКАЛА.
3-3. ЛИНЗЫ. ХОД ЛУЧЕЙ В ЛИНЗАХ.
3-4. ОПТИЧЕСКИЕ ПРИБОРЫ.
3-5. ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ В ЛИНЗАХ.
4. Р Е Ш Е Н И Е З А Д А Ч Ч
А С Т И 2
ЕГЭ – 63 З А Д А Ч
и.
4-1. ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ.
4-2. ПЛОСКИЕ ЗЕРКАЛА.
4-3. ЛИНЗЫ. ХОД ЛУЧЕЙ В ЛИНЗАХ.
4-4. ОПТИЧЕСКИЕ ПРИБОРЫ.
4-5. ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ В ЛИНЗАХ.
5. зАДАЧИ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ –
27 з а
д а
ч.
6. т А Б Л И Ц Ы С Ф О Р М У Л А М И.
| 44 урока по физике для абитуриентов Вы найдете в серии книжек с общим названием “САМ СЕБЕ РЕПЕТИТОР”. |
В КАЧЕСТВЕ |
Р Е Ш Е Н И Е З А
Д А Ч Ч А С Т и
1 ЕГЭ
Задача № 1-4
Световой луч 1 падает под углом α на
переднюю поверхность плоскопараллельной
стеклянной пластинки. На какой угол β от
направления падающего луча отклоняется луч 2,
отражённый от задней поверхности
пластинки и вышедший из неё обратно через
переднюю поверхность?
Рис. 3.
Изобразим на
рисунке ход луча. Проведем вспомогательный луч
3, параллельный падающему лучу и проходящий
через точку выхода луча из стекла. Будем искать
угол β между лучами 2 и 3.
Падающий луч при
входе в стекло преломится под некоторым углом,
после чего под тем же углом отразится от нижней
грани пластинки. Из пластинки луч выйдет под
углом α
(в соответствии с законом
преломления). Угол отклонения направления
вышедшего луча от направления падающего
луча равен углу между двумя лучами 2 и
3.
На рисунке видно,
что этот угол равен β = π − 2α.
Задача № 1-17
Точечный источник S (рис.
16) расположен вблизи системы, состоящей
из двух плоских зеркал З1 и
З2, так, как показано на рисунке.
Сколько изображений даст эта система зеркал?
Рис. 16.
Изображение в
плоском зеркале формирует расходящийся пучок
света, отразившийся от зеркала. Глаз, продолжая
лучи “за зеркало”, видит там мнимое изображение.
При этом для того, чтобы изображение в плоском
зеркале существовало, вовсе не обязательно,
чтобы предмет располагался непосредственно
напротив зеркала. Для того достаточно, чтобы
источник располагался в полупространстве, к
которому обращена отражающая поверхность зеркала.
Из рисунка 17
видно, что источник S
располагается перед зеркалом З1,
но позади зеркала З2, а это
значит, что источник будет давать изображение
только в первом зеркале, а во втором не будет.
Таким образом, данная система зеркал дает
одно изображение
S1.
Рис. 17.
Задача № 1-22
Два плоских зеркала расположили
под прямым углом друг к другу. Докaзaть, что луч,
отразившийся от обоих зеркал, будет параллелен
падающему.
Рис. 20.
Рассмотрим
отражение луча АО1 от двух зеркал
KL и LM, расположенных под прямым углом друг
к другу (рис. 20). Пусть
α
– угол
падения луча АО1 на зеркало KL,
тогда угол отражения луча О1О2от зеркала KL также будет
α.
Далее луч О1О2
падает на зеркало LM. Так как треугольник ΔСО1О2
прямоугольный, то угол падения луча О1О2
равен <СО2О1 = δ = π/2 –
α.
По закону
отражения угол отражения луча О2В также
равен <ВО2С = δ = π/2 – α. Из
рисунка видно, что углы <ВО2С, <СО2О1
и угол φ смежные, откуда получаем
φ
= π – <ВО2С –
<СО2О1
или φ = π – 2δ = π – π/2 + α – π/2 +
α = 2α.
Так как угол
<АО1О2 = φ = 2α, а эти
углы являются внутренними накрест лежащими углами,
следовательно, лучи АО1 и О2В
являются параллельными лучами.
Р Е Ш Е Н И Е З А Д А Ч Ч А С Т И
2
ЕГЭ
Задача № 2-10
Hа дне сосуда,
заполненного водой, лежит плоское зеркало. Человек,
наклонившийся над сосудом, видит изображение своего
глаза в зеркале на расстоянии наилучшего зрения d
= 25 см, когда расстояние от глаза до поверхности воды
h = 5 см. Определить глубину сосуда. Показатель
преломления
воды n = 4/3.
Дано: d = 0,25 м, h = 0,05 м, n =
4/3. Определить b
– ?
Рис. 33.
Для
решения задачи нарисуем рисунок (рис. 33). Мнимое
изображение своего глаза (точки О) наблюдатель
увидит в точке О1 – точке пересечения
двух лучей: О1О и О1СD.
Рассмотрим произвольный луч ОАВСD, выходящий из
глаза и после отражения от зеркала снова попадающий в
глаз. Обычно, при рассмотрении предметов глазом углы
падения и преломления лучей бывают малы, следовательно,
можно пользоваться равенствами: для угла падения
sinα ≈ tgα ≈ α и для угла преломления sinβ
≈ tgβ ≈ β.
Глаз видит изображение точки О в
точке О’ лежащей на продолжении луча CD.
Из треугольника ΔОО1D
выразим катет ОD как
ОD = ОО1·tgα
= d·α
(1).
С другой стороны катет ОD
можно выразить через расстояние h,
глубину сосуда b, угол падения луча
ОА – α и угол преломления луча
АВ –
β.
Предварительно запишем закон преломления луча при переходе
его из воздуха в воду: sinα/sinβ = n или α/β
= n, откуда угол преломления равен β =
α/n. Тогда катет ОD
равен
ОD = 2htgα + 2btgβ
= 2hα + 2bβ, откуда получаем
ОD = 2α(h +
b/n) (2).
Приравниваем правые части выражений
(1) и (2)
Задача № 2-26
Расстояние между точечным источником света и экраном
L. Между ними помещают собирающую линзу, которая
дает на экране резкое изображение точечного источника
при двух положениях линзы. Определите фокусное
расстояние F линзы, если расстояние между
указанными положениями линзы b.
Дано: L, b. Определить
F – ?
Рис. 48.
При решении данной задачи нам приходится иметь дело с
пятью неизвестными: d1, d2, f1,
f2 и F.
Следовательно, для
успешного решения задачи, нам необходимо построить пять
независимых уравнений.
Воспользуемся рис. 48.
На рисунке представлены два положения линзы I
и II, при которых получаются резкие
изображения. Строим
уравнения:
Исключаем неизвестные: подставляем уравнения (1), (2) и
(3) в уравнения (4) и (5).
телефон:
+79175649529, почта:
gaegoralev@mail.ru
Источник