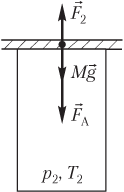Идеальный газ в сосуде с поршнем

5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
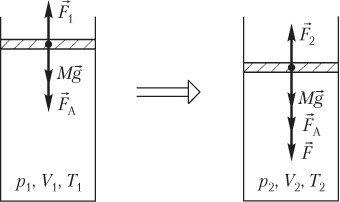
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
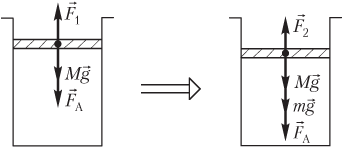
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
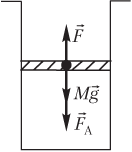
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник
8748. Объем сосуда с идеальным газом уменьшили вдвое, выпустив половину газа и поддерживая температуру газа в сосуде постоянной. Как изменятся в результате этого давление газа в сосуде и его внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8748.
8780. В цилиндрическом сосуде под поршнем находится газ. Поршень не закреплен и может перемещаться в сосуде без трения (см. рисунок). В сосуд закачивается еще такое же количество газа при неизменной температуре. Как изменится в результате этого давление газа и концентрация его молекул?

Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8780.
8812. Аргон помещают в открытый сверху сосуд под легкий подвижный поршень и начинают охлаждать, Давление воздуха, окружающего сосуд, равно 105 Па. Начальный объем газа 9 л, начальная температура 450 К. Масса газа в сосуде остается неизменной. Трением между поршнем и стенками сосуда пренебречь.
Установите соответствие между физическими величинами, характеризующими аргон, и формулами, выражающими их зависимость от абсолютной температуры Т газа в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) внутренняя энергия газа ( U(T) )
Б) объем газа ( V(T) )
ФОРМУЛЫ
1) ( dT, d = ) 3 Дж/К
2) ( frac{b}{T}, b = ) 4050 м3 ⋅ K
3) ( at, a = ) 2 ⋅ 10-5 м3/K
4) ( cT, c = ) 20 Дж/К

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8812.
8844. На рисунке показан процесс изменения состояния одного моля одноатомного идеального газа (U – внутренняя энергия газа; p – его давление). Как изменятся в ходе этого процесса объем и теплоемкость газа? Для каждой величины определите соответствующий характер изменения:

1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8844.
8876. В цилиндре под поршнем находится твердое вещество. Цилиндр поместили в раскаленную печь. На рисунке показан график изменения температуры T вещества по мере поглощения им количества теплоты Q. Какие участки графика соответствуют нагреванию вещества в газообразном состоянии и кипению жидкости?

ТЕПЛОВЫЕ ПРОЦЕССЫ
А) кипение жидкости
Б) нагревание вещества в газообразном состоянии
УЧАСТКИ ГРАФИКА
1) 1
2) 2
3) 3
4) 4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8876.
8908. При исследовании изопроцессов использовался закрытый сосуд переменного объема, заполненный аргоном и соединенный с манометром. Объем сосуда медленно уменьшают, сохраняя температуру аргона в нем неизменной. Как изменятся при этом внутренняя энергия аргона в сосуде и концентрация его молекул?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8908.
8940. В ходе адиабатного процесса внутренняя энергия 1 моль разреженного гелия увеличивается. Как изменяются при этом температура гелия и его давление?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8940.
8972. Установите соответствие между процессами в идеальном газе и значениями физических величин, характеризующих эти процессы (( Delta U ) – изменение внутренней энергии; ( A ) работа газа, ( nu ) – количество газа).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) изотермическое сжатие при ( nu = const )
Б) изобарное расширение при ( nu = const )
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
1) ( Delta U > 0,~A = 0 )
2) ( Delta U > 0,~A > 0 )
3) ( Delta U = 0,~A > 0 )
4) ( Delta U = 0,~A

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8972.
9004. Установите соответствие между процессами в идеальном газе и значениями физических величин, характеризующих эти процессы (( Delta U ) – изменение внутренней энергии; ( A ) – работа газа, ( upsilon ) – количество газа).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) адиабатическое сжатие при ( nu = const )
Б) изохорное нагревание при ( nu = const )
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
1) ( Delta U > 0,~A = 0 )
2) ( Delta U > 0,~A > 0 )
3) ( Delta U = 0,~A > 0 )
4) ( Delta U > 0,~A

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9004.
9036. Температуру холодильника теплового двигателя, работающего по циклу Карно, увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД теплового двигателя и количество теплоты, отданное газом за цикл холодильнику?
Для каждой величины определите соответствующий характер изменения:
1) не изменилась
2) уменьшилась
3) увеличилась


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9036.
Для вас приятно генерировать тесты, создавайте их почаще
Источник
Изобарный процесс
Заполните пропуск в тексте.
Повторите определение изобарного процесса.
Процесс изменения состояния термодинамической системы данной массы при называют изобарным.
постоянном давлении
постоянной температуре
постоянном объёме
Газовые законы
Заполните таблицу.
Повторите газовые законы.
| Закон | Изопроцесс | Формула |
|---|---|---|
$frac{V}{T}=const$ | ||
Изотермический | ||
Шарля |
Бойля–Мариотта
$frac{p}{T}=const$
Изохорный
Изобарный
Гей-Люссака
$pV=const$
Физические величины
Установите соответствие между физическими величинами и их единицами измерения.
Вспомните основные величины и единицы их измерения.
Уравнение состояния идеального газа
Соедините попарно физическую величину с её значением так, чтобы получились верные ответы.
1. В баллоне объёмом 2 $м^3$ находится 2 кг молекулярного кислорода при давлении $10^5$ Па. Какова температура кислорода (ответ в К)?
2. В баллоне ёмкостью 10 л находится углекислый газ при температуре 17 $^circ$ С под давлением 107 Па. Какой объём займёт этот газ при нормальных условиях (ответ в $м^3$)?
3. В закрытом сосуде объёмом 10 литров находится 2 моль азота. Температура газа равна 27 $^circ$ С. Чему равно давление газа (ответ в кПа)?
Повторите уравнение состояния идеального газа.
Изопроцессы
Соедините попарно фигуры так, чтобы каждому изопроцессу соответствовала формула.
Вспомните определения изопроцессов.
Основные величины МКТ
Решите кроссворд.
Вспомните основные величины МКТ и единицы их измерения.
Физические термины
Выделите мышкой 5 слов, которые относятся к теме урока.
1. Состояние вещества, в котором расстояние между атомами и молекулами в среднем во много раз больше размеров самих молекул.
2. Мельчайшая частица вещества.
3. Итальянский учёный XIX века, в честь которого названа постоянная, показывающая, какое количество атомов или молекул содержится в 1 моле вещества.
4. Синоним слова «корпускула».
5. Единица измерения количества вещества в СИ.
Повторите авторов законов и определения.
Газовые законы
Заполните пропуски в тексте, выбрав правильные варианты ответа из выпадающего меню.
Повторите газовые законы.
В сосуде под поршнем находится газ. При его изотермическом расширении давление газа на стенки сосуда
, температура
, объём газа
.
Измерительные приборы
Установите соответствие между физическими величинами и приборами для их измерения.
Повторите определения давления, температуры.
Экспериментальные исследования
Выберите верные утверждения, которые соответствуют результатам проведённых экспериментальных исследований.
В сосуде неизменного объема при комнатной температуре находилась смесь водорода и гелия, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль водорода. Газы считаются идеальными, а их температура постоянной.
Вспомните закон Гей-Люссака, закон Дальтона, определение парциального давления.
Давление смеси газов в сосуде не изменилось
В начале опыта концентрации газов были одинаковые
Парциальное давление водорода уменьшилось
Концентрация гелия увеличилась
В начале опыта массы газов были одинаковые
Изотермический процесс
На рисунке приведены графики двух изотермических процессов, проводимых с одной и той же массой газа. На основании графиков выберите верные утверждения о процессах, происходящих с газом.

Вспомните график изотермического процесса, на графике посмотрите направление стрелки.
Никаких выводов по графику сделать нельзя
Процесс 2 идёт при более высокой температуре
Процесс 1 идёт при более высокой температуре
Оба процесса идут при одной и той же температуре
В процессе 1 объём увеличивается
Газовые законы
Выделите мышкой 5 слов, которые относятся к теме урока.
1. Один из учёных, открывших изотермический процесс.
2. Единица измерения абсолютной температуры.
3. Параметр состояния газа постоянный в изохорном процессе.
4. Процессы, происходящие при постоянном значении одного из макропараметров состояния
5. Параметр состояния газа постоянный в изотермическом процессе.
Вспомните газовые законы.
Изопроцессы
Выделите мышкой 4 слова, которые относятся к теме урока.
1. Макроскопический параметр постоянный во всех изопроцессах.
2. Величины, характеризующие состояние газа.
3. График изопроцесса с постоянным объёмом.
4. График изопроцесса с постоянным давлением.
Вспомните изопроцессы.
Газовые законы
Выделите мышкой 4 слова, которые относятся к теме урока.
1. То, из чего состоит молекула.
2. Масса моля вещества.
3. Упрощённая модель реального газа.
4. Учёный, открывший взаимосвязь между давлением и температурой при постоянном объёме.
Повторите конспекты.
Источник