Имеются 2 сосуда содержащие 42 и 6 раствора кислоты

ÐадаÑа â807 из 1084 |
ÐмеÑÑÑÑ Ð´Ð²Ð° ÑоÑÑда, ÑодеÑжаÑие 10 кг и 16 кг ÑаÑÑвоÑа киÑлоÑÑ ÑазлиÑной конÑенÑÑаÑии. ÐÑли Ð¸Ñ ÑлиÑÑ Ð²Ð¼ÐµÑÑе, Ñо полÑÑиÑÑÑ ÑаÑÑвоÑ, ÑодеÑжаÑий 55% киÑлоÑÑ. ÐÑли же ÑлиÑÑ ÑавнÑе маÑÑÑ ÑÑÐ¸Ñ ÑаÑÑвоÑов, Ñо полÑÑеннÑй ÑаÑÑÐ²Ð¾Ñ Ð±ÑÐ´ÐµÑ ÑодеÑжаÑÑ 61% киÑлоÑÑ. СколÑко килогÑаммов киÑлоÑÑ ÑодеÑжиÑÑÑ Ð² пеÑвом ÑаÑÑвоÑе?
РеÑение задаÑи:
Ðведем обознаÑениÑ:
x – конÑенÑÑаÑÐ¸Ñ ÐºÐ¸ÑлоÑÑ Ð² пеÑвом ÑоÑÑде.
10x – маÑÑа киÑлоÑÑ Ð² 10 кг ÑаÑÑвоÑа в пеÑвом ÑоÑÑде, Ñ.е. Ñо ÑÑо надо найÑи в задаÑе.
y – конÑенÑÑаÑÐ¸Ñ ÐºÐ¸ÑлоÑÑ Ð²Ð¾ вÑоÑом ÑоÑÑде.
16y – маÑÑа киÑлоÑÑ Ð² 16 кг ÑаÑÑвоÑа во вÑоÑом ÑоÑÑде.
СоÑÑавим ÑÑавнение Ð´Ð»Ñ Ð¿ÐµÑвого ÑÑловиÑ:
10x+16y=26*0,55 (26 – ÑÑо маÑÑа нового ÑаÑÑвоÑа 10+16, 0,55 – конÑенÑÑаÑÐ¸Ñ Ð½Ð¾Ð²Ð¾Ð³Ð¾ ÑаÑÑвоÑа).
10x+16y=14,3
10x=14,3-16y
СоÑÑавим ÑÑавнение Ð´Ð»Ñ Ð²ÑоÑого ÑÑловиÑ:
10x+10y=20*0,61
10x+10y=12,2
ÐодÑÑавлÑем во вÑоÑое ÑÑавнение знаÑение 10Ñ
:
14,3-16y+10y=12,2
14,3-6y=12,2
6y=14,3-12,2
6y=2,1
y=0,35
ÐодÑÑавлÑем знаÑение y в пеÑвое ÑÑавнение:
10x=14,3-16y
10x=14,3-16*0,35
10x=8,7
ÐÑвеÑ: 8,7
ÐоделиÑеÑÑ ÑеÑением
ÐÑиÑоединÑйÑеÑÑ Ðº нам…
ÐÑ Ð¼Ð¾Ð¶ÐµÑе поблагодаÑиÑÑ Ð°Ð²ÑоÑа, напиÑаÑÑ Ñвои пÑеÑензии или пÑÐµÐ´Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°
ÑÑÑаниÑе ‘ÐÑо нађ
ÐÑÑгие задаÑи из ÑÑого Ñаздела

ÐадаÑа â272C8D

Ðа ÑиÑÑнке изобÑажÑн ÐºÐ¾Ð»Ð¾Ð´ÐµÑ Ñ Â«Ð¶ÑÑавлÑм». ÐоÑоÑкое плеÑо Ð¸Ð¼ÐµÐµÑ Ð´Ð»Ð¸Ð½Ñ 1 м, а длинное плеÑо â 3 м. Ðа ÑколÑко меÑÑов опÑÑÑиÑÑÑ ÐºÐ¾Ð½ÐµÑ Ð´Ð»Ð¸Ð½Ð½Ð¾Ð³Ð¾ плеÑа, когда ÐºÐ¾Ð½ÐµÑ ÐºÐ¾ÑоÑкого поднимеÑÑÑ Ð½Ð° 0,5 м?

ÐадаÑа â1B4DE1
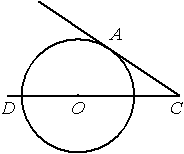 ÐайдиÑе Ñгол ÐСÐ, еÑли его ÑÑоÑона СРкаÑаеÑÑÑ Ð¾ÐºÑÑжноÑÑи, Ð â ÑенÑÑ Ð¾ÐºÑÑжноÑÑи, а дÑга AD окÑÑжноÑÑи, заклÑÑÑÐ½Ð½Ð°Ñ Ð²Ð½ÑÑÑи ÑÑого Ñгла, Ñавна
ÐайдиÑе Ñгол ÐСÐ, еÑли его ÑÑоÑона СРкаÑаеÑÑÑ Ð¾ÐºÑÑжноÑÑи, Ð â ÑенÑÑ Ð¾ÐºÑÑжноÑÑи, а дÑга AD окÑÑжноÑÑи, заклÑÑÑÐ½Ð½Ð°Ñ Ð²Ð½ÑÑÑи ÑÑого Ñгла, Ñавна
110°.

ÐадаÑа â1A8C8D
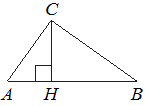 Ðа гипоÑенÑÐ·Ñ AB пÑÑмоÑголÑного ÑÑеÑголÑника ABC опÑÑена вÑÑоÑа CH, AH=4, BH=64. ÐайдиÑе CH.
Ðа гипоÑенÑÐ·Ñ AB пÑÑмоÑголÑного ÑÑеÑголÑника ABC опÑÑена вÑÑоÑа CH, AH=4, BH=64. ÐайдиÑе CH.

ÐадаÑа â2DC92C
 ÐлоÑÐ°Ð´Ñ Ð¿ÑÑмоÑголÑного ÑÑеÑголÑника Ñавна 800√3. Ðдин из оÑÑÑÑÑ
Ñглов Ñавен 30°. ÐайдиÑе Ð´Ð»Ð¸Ð½Ñ ÐºÐ°ÑеÑа, лежаÑего напÑоÑив ÑÑого Ñгла.
ÐлоÑÐ°Ð´Ñ Ð¿ÑÑмоÑголÑного ÑÑеÑголÑника Ñавна 800√3. Ðдин из оÑÑÑÑÑ
Ñглов Ñавен 30°. ÐайдиÑе Ð´Ð»Ð¸Ð½Ñ ÐºÐ°ÑеÑа, лежаÑего напÑоÑив ÑÑого Ñгла.

ÐадаÑа â03F9DB
Ð ÑавнобедÑенной ÑÑапеÑии оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ ÑÐ°Ð²Ð½Ñ 4 и 8, а один из Ñглов Ð¼ÐµÐ¶Ð´Ñ Ð±Ð¾ÐºÐ¾Ð²Ð¾Ð¹ ÑÑоÑоной и оÑнованием Ñавен 45°. ÐайдиÑе плоÑÐ°Ð´Ñ ÑÑапеÑии.
Источник
Задачи на проценты, сплавы и смеси
1
Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
2
Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
3
При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
4
На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
5
Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
6
Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
7
Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
8
Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
9
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
10
Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?
11
Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
12
Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
13
Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
14
Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
15
Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
16
Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
17
Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
18
Свежие фрукты содержат 88 % воды, а высушенные — 30 %. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
19
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
20
Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?
Задачи на проценты, сплавы и смеси
1. Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Решение.
Пусть ![]() кг и
кг и ![]() кг — массы первого и второго растворов, взятые при смешивании. Тогда
кг — массы первого и второго растворов, взятые при смешивании. Тогда ![]() кг — масса полученного раствора, содержащего
кг — масса полученного раствора, содержащего ![]() кг кислоты. Концентрация кислоты в полученном растворе 20 %, откуда
кг кислоты. Концентрация кислоты в полученном растворе 20 %, откуда
![]()
Решим систему двух полученных уравнений:


Замечание. Решение можно сделать несколько проще, если заметить, что из полученных уравнений следует: ![]() , откуда
, откуда ![]() . Первое уравнение принимает вид
. Первое уравнение принимает вид ![]() , откуда
, откуда ![]() .
.
Ответ: 2 кг.
2. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Решение.
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение:
![]()
Выразим x через y:
![]()
Следовательно, отношение, в котором нужно взять сплавы:
![]()
Ответ: ![]()
3. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
Решение.
Пусть первый раствор взят в количестве ![]() грамм, тогда он содержит 0,2
грамм, тогда он содержит 0,2![]() грамм чистой кислоты, а второй раствор взят в количестве
грамм чистой кислоты, а второй раствор взят в количестве ![]() грамм, тогда он содержит 0,5
грамм, тогда он содержит 0,5![]() грамм чистой кислоты. При смешивании двух этих растворов получится раствор массой
грамм чистой кислоты. При смешивании двух этих растворов получится раствор массой ![]() +
+ ![]() грамм, по условию задачи, он содержит 0,3(
грамм, по условию задачи, он содержит 0,3(![]() +
+ ![]() ) чистой кислоты. Следовательно, можно составить уравнение:
) чистой кислоты. Следовательно, можно составить уравнение:
![]()
Выразим ![]() через
через ![]() :
: ![]() Следовательно, отношение, в котором были взяты растворы:
Следовательно, отношение, в котором были взяты растворы: ![]()
Ответ: ![]()
4. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
Решение.
Заметим, что победителем на выборах окажется Зайцев. Пусть количество голосов, отданных за Зайцева равно ![]() . Тогда за Журавлёва и Иванова вместе отдали
. Тогда за Журавлёва и Иванова вместе отдали ![]() . Процент голосов, отданных за Зайцева
. Процент голосов, отданных за Зайцева ![]()
Ответ: 75%.
5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Решение.
Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего — (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором — 0,13(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение:
![]()
Откуда ![]()
Масса третьего сплава равна 16 кг.
Ответ:16 кг.
6. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
Решение.
Свежие фрукты содержат 20% питательного вещества, а высушенные — 72%. В 288 кг свежих фруктов содержится 0,2 · 288 = 57,6 кг питательного вещества. Такое количество питательного вещества будет содержаться в ![]() кг высушенных фруктов.
кг высушенных фруктов.
Ответ: 80.
Ответ: 80
7. Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли ![]() г 10-процентного раствора, тогда взяли и
г 10-процентного раствора, тогда взяли и ![]() г 12-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 12-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится ![]() г, а во втором —
г, а во втором — ![]() г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна ![]() или 11%.
или 11%.
Ответ: 11%.
8. Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
Решение.
Заметим, что сухая часть свежих фруктов составляет 14%, а высушенных — 77%. Значит, для приготовления 72 кг высушенных фруктов требуется ![]() кг свежих.
кг свежих.
Ответ: 396 кг.
9. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:

Таким образом, в первом растворе содержится ![]() килограмма кислоты.
килограмма кислоты.
Ответ: 8,7.
Ответ: 8,7
10. Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, в первом растворе содержится ![]() килограмма кислоты
килограмма кислоты
Ответ: 2,6
Ответ: 2,6
11. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, во втором растворе содержится ![]() килограмма кислоты
килограмма кислоты
Ответ: 19,5
Ответ: 19,5
12. Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:

Таким образом, во первом растворе содержится ![]() килограмма кислоты.
килограмма кислоты.
Ответ: 2.
Ответ: 2
13. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, во втором растворе содержится ![]() килограмма кислоты
килограмма кислоты
Ответ: 15,6
Ответ: 15,6
14. Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, во втором растворе содержится ![]() килограмма кислоты
килограмма кислоты
Ответ: 18,6
Ответ: 18,6
15. Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, в первом растворе содержится ![]() килограмов кислоты
килограмов кислоты
Ответ: 11
Ответ: 11
16. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, во втором растворе содержится ![]() килограммов кислоты
килограммов кислоты
Ответ: 23,1
Ответ: 23,1
17. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:

Таким образом, во втором растворе содержится ![]() килограмма кислоты
килограмма кислоты
Ответ: 4,2
Ответ: 4,2
18. Свежие фрукты содержат 88 % воды, а высушенные — 30 %. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
Решение.
Заметим, что сухая часть свежих фруктов составляет 12%, а высушенных — 70%. Значит, для приготовления 6 кг высушенных фруктов требуется ![]() кг свежих.
кг свежих.
Ответ: 35 кг.
Ответ: 35
19. Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли ![]() г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и ![]() г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится ![]() г, а во втором —
г, а во втором — ![]() г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна ![]() или 58%.
или 58%.
Ответ: 58.
Ответ: 58
20. Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?
Решение.
Свежие фрукты содержат 7% питательного вещества, а высушенные — 84%. В 252 кг свежих фруктов содержится 0,07 · 252 = 17,64 кг питательного вещества. Такое количество питательного вещества будет содержаться в ![]() кг высушенных фруктов.
кг высушенных фруктов.
Ответ: 21.
Источник
