Исследование процесса вытекания воды из отверстия в сосуде
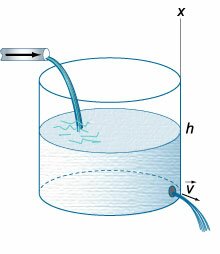
Закон Торричелли Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей, в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой: [v = sqrt {2gh} ,] где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
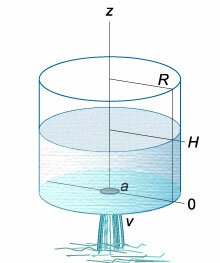
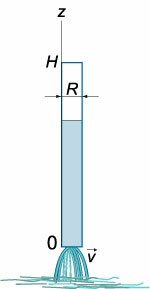
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме. В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому, формула Торричелли часто записывается с дополнительным множителем (varphi:) [v = varphisqrt {2gh} ,] где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках. Вытекание жидкости из тонкой трубки Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные поверхностным натяжением и смачиванием вследствие контакта со стенками трубки. Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть [v = kh,] где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки. Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого). Дифференциальное уравнение вытекания жидкости Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
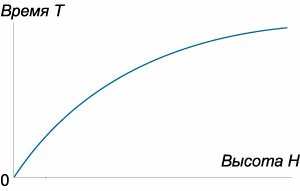
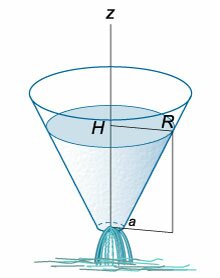
Скорость жидкости описывается формулой Торричелли: [v = sqrt {2gz} ,] где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением: [q = – pi {a^2}sqrt {2gz} .] Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает, что уровень жидкости уменьшается по мере ее вытекания из резервуара. Уравнение баланса жидкости в резервуаре описывается следующим образом: [frac{{dV}}{{dt}} = q.] Поскольку изменение объема (dV) можно выразить как [dV = Sleft( z right)dz,] то мы получаем дифференциальное уравнение [frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).] Подставим функцию (qleft( z right)) в это уравнение: [frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .] Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно [Sleft( z right) = pi {R^2},] где (R) − радиус основания цилиндра. Тогда [require{cancel} cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} . ] В результате получаем уравнение с разделяющимися переменными: [frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.] Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:) [ {intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};; {Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};; {Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};; {Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.} ] Отсюда следует выражение для полного времени вытекания жидкости (T:) [T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .] Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, ) которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.) Аналогично можно описать вытекание жидкости и из сосуда другой формы. | Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.) Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением [Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),] где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.) Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать: [qleft( z right) = – pi {a^2}sqrt {2gz} ,] где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник (рисунок (6) выше). Из подобия треугольников следует, что [frac{R}{H} = frac{r}{z}.] Следовательно, площадь поверхности жидкости на высоте (z) будет равна [ {Sleft( z right) = pi {r^2} } = {pi {left( {frac{{Rz}}{H}} right)^2} } = {frac{{pi {R^2}{z^2}}}{{{H^2}}}.} ] Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем: [frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .] После простых преобразований получаем следующее дифференциальное уравнение: [{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.] Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:) [ {intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};; {Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};; {Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};; {Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};; {Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .} ] Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно, время падения описывается формулой: [T = sqrt {frac{{2H}}{g}}. ] Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли? | Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
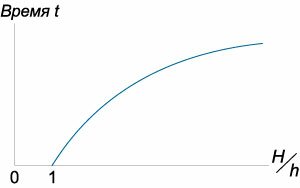
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме: [Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).] В данном случае площадь поперечного сечения (Sleft( z right)) является константой: [Sleft( z right) = S = pi {R^2},] и поток жидкости, вытекающей из сосуда, определяется формулой: [qleft( z right) = – kz,] где (k) зависит от размера отверстия, смачиваемости и других параметров. В результате получаем простое дифференциальное уравнение: [pi {R^2}frac{{dz}}{{dt}} = – kz,] или после разделения переменных: [frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.] Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:) [ {intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};; {Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};; {Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.} ] Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.) Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли. Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.) |
Источник
Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки (коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре, превращается в кинетическую энергию свободной струи.
Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).
Рис. 5.1. Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.
Рис. 5.2. Истечение через круглое отверстие
Степень сжатия оценивается коэффициентом сжатия.
где Sс и Sо – площади поперечного сечения струи и отверстия соответственно; dс и dо – диаметры струи и отверстия соответственно.
Скорость истечения жидкости через отверстие такое отверстие
где Н – напор жидкости, определяется как
φ- коэффициент скорости
где α – коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.
В итоге получаем расход
где ΔР – расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача – определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
где ν – кинематическая вязкость.
| Рис. 5.3. Зависимость ε, φ и от числа Reu | Рис. 5.4. Инверсия струй |
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).
Рис. 5.5. Схема несовершенного сжатия струи
Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в п.5.1.
При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной Н.Е. Жуковским:
где n – отношение площади отверстия Sо к площади поперечного сечения резервуара S1
Расход жидкости при несовершенном сжатии
где напор Н нужно находить с учетом скоростного напора в резервуаре
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное отверстие.
Рис. 5.6. Истечение по уровень
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
где φ – коэффициент скорости;
Н – расчетный напор,
Расход жидкости равен
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис.5.7).
Рис. 5.7. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка
P2 – P1 0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому
Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.5.8).
Рис. 5.8. Второй режим истечения через насадок
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих коэффициентов.
Рис. 5.9. Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся конические; в – коноидальные; г – внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
Рис. 5.10. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровнеS, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:
где dh – изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:
где l – длина цистерны; D – диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным
Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия, перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения, истечение из которых и рассмотрим.
Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором влияет на истечение.
Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением (рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды (рис. 5.14).
Рис. 5.13. Истечение из-под затвора через незатопленное отверстие
Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости. На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей зависимостью:
hc = ε’a
где ε’ – коэффициент вертикального сжатия струи.
Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать ε’ = 0,64.
Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после преобразований получим:
где φ – коэффициент скорости,
где Н0 – напор с учетом скорости подхода,
Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:
где S – площадь отверстия, S = ab.
Рис. 5.14. Истечение из-под затвора при затопленном отверстии
При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:
где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под затвора струи.
Глубина hz определяется из зависимости
в которой
а hб – глубина в отводящем канале (бытовая глубина).
Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку, имеет вид
На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и уравнения, по которым вычисляется давление струи на соответствующую поверхность.
Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).
В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения. В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец, в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.
Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью
Рис. 5.16. Составные части свободной струи
Источник