Истечение газа из отверстия в сосуде
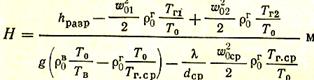
УДК 536.35
А.М. Гущин1, Н.В. Володарец2, А.П. Соломин3, А.С. Балагура4, Е.А. Бондарь5
1 Донецкий институт железнодорожного транспорта, г. Донецк, Украина,
2 Донецкая академия автомобильного транспорта, г. Донецк, Украина,
3 Донецкий институт железнодорожного транспорта, г. Донецк, Украина,
4 Донецкий институт железнодорожного транспорта, г. Донецк, Украина,
5
Введение.
Истечение газов характеризуется прохождением их через отверстие или короткие патрубки отличающиеся тем, что в процессе прохождения можно пренебречь аэродинамическим сопротивлением и процессами теплообмена.
Процессы истечения на практике используются, для превращения потенциальной энергии давления газа в ёмкости в кинетическую энергию движения газового потока, которая на потоках турбинного колеса превращается во вращающий момент вала этого колеса. Этот процесс осуществляется в системе турбонаддува на тепловозах.
В тех случаях, когда истечение газа происходит из закрытой емкости, в ней снижается давление и температура среды, что приводит к изменению интенсивности процесса истечения.
Постановка задачи.
В термодинамике известна закономерность истечения газов из ёмкости фиксированными значениями температуры и давления газа. При изменяющимся во времени давлении и температуры газов необходимо решать сопряженную задачу собственного истечения газа через патрубок и изменение параметров состояния газа в ёмкости. Процесс истечения газа из ёмкости является гладким. Выделяют две области истечения: закритическое и докритическое. При докритическом истечении интенсивность истечения зависит от параметров состояния газа в ёмкости и давления в среде, в которую происходит истечение. При закретическом истечении интенсивность истечения не зависит от давления в среде истечения. Границей этих двух областей истечения, служит критическое отношение давления в среде истечения и давления в ёмкости из которой происходит истечение
где Рс – давление в среде в которую осуществляется истечение газа;
Ркр – давление газа в ёмкости из которой происходит истечение;
βкр – критическое отношение.
Если значение отношений давлений больше βкр имеет место докритическое отношение, если отношение меньше βкр имеет место закритическое истечение. Значение критического отношения давлений βкр, а так же значения показания адиабаты «К»для разных газов приведено ниже в таблице 1.
Таблица 1
| Атомность газа | Значение показания адиабаты «К» | Критическое отношение давлений βкр |
| Одноатомный | 1.66 | 0.49 |
| Двухатомный | 1.4 | 0.528 |
| Трехатомный и перегретый пар | 1.3 | 0.546 |
В процессе истечения газа из ёмкости происходит снижение давления и его температуры, что неизбежно приводит к появлению теплообмена газа с окружающей средой, а это непосредственно влияет на давление газа в ёмкости и изменению на течение m(кг/с).
Влияние теплообмена на процесс истечения можно учесть двумя способами:
Заданием закона теплообмена или заданием закона изменения параметров состояния газа в ёмкости.
Из изученной литературы об истеченении газа из ёмкости можно выделить четыре задачи:
1. Описание процесса истечения в закритической области при заданности закона соотношения между параметрами состояния газа в ёмкости;
2. Описание процесса истечения в закритической области при заданном законе теплообмена газа в ёмкости с окружающей средой;
3. Описание процесса истечения газа в докритической области при заданном законе соотношения между параметрами газа в ёмкости;
4. Описание процесса истечения газа в докритической области при заданном законе теплообмена газа в ёмкости с окружающей средой.
Цель исследования: Разработать расчетные зависимости для определения изменяющихся во времени давления газа в ёмкости, его температуры, интенсивности истечения.
При решении поставленной задачи использовались известные в термодинамике зависимости:
– уравнение состояния идеального газа для 1-го кг газа и для G кг газа, соответственно:
(1)
где P – давление газа;
– удельный объём газа;
R – удельная газовая постоянная;
T – температура газа;
V – объём ёмкости из которой происходит истечение газа
G – масса газа в объёме V.
– интенсивность истечения газа при фиксированных значениях температуры и давления в закритической области:
(2)
где – коэффициент сопла;
– площадь поперечного выходного сечения сопла;
В качестве заданного соотношения между параметрами газа в ёмкости могут быть соотношения их для изотермического адиабатного или политропного процессов. Политропный процесс можно рассматривать как обобщающий процесс, а два других упомянутых выше можно рассматривать как частные случаи политропного. В связи с этим, соотношение между давлением газа и температурой получается уравнение политропного процесса:
(3)
где n – показатель политропы.
Значение показателя политропы в общем случае может изменятся в широких пределах. Его значение зависит в основном от характера теплообмена газа в ёмкости с окружающей средой. Значение этого показателя находят на практике экспериментальным путём для сходных условий изменения состояния газа.
Находим зависимость описывающую изменение во времени давления газа в ёмкости.
Дифференцируем уравнение (1)
(4)
Члены уравнения (4) разделим на члены уравнения(1), получим:
(5)
Отношение получаем путём дифференцирования уравнения (3)
(6)
Величину dG можно выразить соотношением:
dG=-mdτ (7)
где m – интенсивность истечения (кг/с);
τ – текущее время.
Знак (-) в уравнении (7) поставлен в связи с тем, что массовый расход газа в ёмкости при его истечении уменьшается и его изменение dG должно быть отрицательной величной.
В выражении для m (2) сделаем замену:
(8)
Тогда выражение (7) преобразуется в следующую форму:
(9)
Соотношение в (9) заменим по уравнению (1)
(10)
Значение температуры Т заменим через давление газа Р в соответствии с уравнением (3)
(11)
где Р1 и Т1– начальные значения давления температуры в ёмкости
Соотношение (11) представляем в (9)
; (12)
Текущее значение массы газа в ёмкости выразим из уравнения (1)
(13)
Значение температуры Т в формуле (13) выразим из уравнения (3)
(14)
Соотношение (6), (12) и (14) выразим в уравнении (5)
(15)
После определенных алгебраических преобразований из уравнения (15) получаем:
(16)
Уравнение (16) дифференциальное уравнение с раздельными переменными.
Интегрируем уравнение (16). После интегрирования этого уравнения и некоторых алгебраических преобразований получаем:
(17)
В уравнении (17) выполним замену
(18)
В уравнении (17) преобразуем:
(19)
Таким образом получена зависимость описывающая характер изменения давления в емкости для области закритического истечения для случая, когда соотношение между температурой и давлением газа в емкости соответствует политропному процессу. Изменение температуры во времени найдется из совместного решения уравнений (3) и (19)
(20)
Остаточная масса газа в ёмкости после времени истечения определяется из совместного решения уравнений (13), (19) и (20)
(21)
Интенсивность истечения газа (m) определяется из совместного решения уравнений (2),(8), (11) и (19)
(22)
Формулы (19)…(20) справедливы при истечении до момента когда давление в ёмкости сжимается до критического истечения в соответствии с формулой:
(23)
Из уравнения(19), можно найти время истечения, при котором давление в ёмкости снизится до критического значения. Рассмотрев формулу (19) предположим, что время истечения будет равным:
(24)
Формулы (17)…(24) получены для случая политропного изменения параметров газа в ёмкости. Предположим, что истечение организовано так, что выполнена совершенная теплоизоляция ёмкости. Соотношение между параметрами соотношения в этом случае будет соответствовать уравнению адиабатного процесса. При этом уравнение будут иметь ту же форму, только вместо показателя политропы «n» необходимо подставлять значение показателя адиабаты «К» из таблицы 1.
Далее выведем уравнение изменения во времени давления, интенсивности истечения газа в ёмкости для случая неизменной температуры газа в ней. В качестве исходных используем выше приведенные уравнения (1) и (2)
(25)
Бесконечно малое изменение массы газа в ёмкости вырази через интенсивность истечения «m»
(26)
Интенсивность истечения «m» в соответствиями с формулами (2) и (8) выразится соотношением
(27)
Удельный объём выразим из уравнения (1)
(28)
Тогда значение «m» выразим соотношением
(29)
Соотношение (26) и (29) подставим в (25)
(30)
После интегрирования уравнения (30) получим
(31)
Интенсивность истечения «m» по уравнению (2) с учетом обозначения (8) выразим соотношением:
(32)
Из уравнения (1) находим
(33)
Соотношение (33) подставляем в формулу (32):
(34)
C учетом зависимости (31):
(35)
Из формулы (31) определяем время за которое сначала истечения давления снизится до критического значения. Принимая во внимание соотношение:
(36)
Из уравнения (31) находим искомое время
(37)
Вывод: Приведенные выше результаты исследований позволяют сделать следующие выводы:
1. Показано, что изменение параметров состояния газа в ёмкости определяется не только истечением газа из ёмкости но и неизбежным теплообменом газа в ёмкости с окружающей средой, и для определения зависимостей, описывающих процессы в ёмкости, необходимо выполнить решение спряженной задачи, связывающей процесс истечения с процессом изменения параметров состояния в ёмкость, из которой происходит истечение газа.
2. Изменение параметров состояния газа в ёмкости можно связывать определенными соотношениями имеющими место при адиабатном, изотермическом или политропным процессами или уравнение теплообмена газов в ёмкости с окружающей средой. Закономерность истечения газов иметь две формы: для закритеческого и докритического истечения.
Таким образом, процесс изменения состояния газа в ёмкости распадается на четыре отдельных задачи, отражающие характер истечения газа и характер изменения параметров состояния в ёмкости, из которой происходит истечение газа.
3. Решена задача 1 которая характеризуется истечением в закритической области и заданием политропного, адиабатного и изотермического процесса в ёмкости. Получены зависимости описывающие изменение во времени давления, температуры газа, уравнением интенсивности истечения, количеством остаточного газа в ёмкости, а так же зависимость для определения времени, за которое давление газа снижается до критического значения.
Читайте также:
Рекомендуемые страницы:
©2015-2021 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-11
Нарушение авторских прав и Нарушение персональных данных
Источник
41. 1 Основные теоретические сведения
Давление условно называется высоким, если при реализации соответствующей ему потенциальной энергии в энергию кинетическую плотность и температура газа, уменьшаясь, претерпевают существенные изменения.
В резервуаре или канале, из которого происходит истечение, давление, плотность, температура и скорость движения газа равны соответственно р1, r1, Т1, v1.
р, r, Т, v – те же самые параметры у выхода из отверстия (или на срезе сопла). Размеры сосуда настолько велики, что скорость газа внутри сосуда v1 » 0.
Скорость истечения газа равна:
v = , (41.1)
где k – показатель адиабаты.
Согласно уравнению состояния = R × T1. Тогда скорость истечения может быть определена
v = .
Из формулы (41.1) следует, что с уменьшением давления вне сосуда, скорость истечения газа растёт, достигая максимального значения при истечении в вакуум (р = 0)
vmax = . (41.2)
Скорость звука а – это скорость распространения упругих колебаний. Она связана с давлением и плотностью среды зависимостью а2 = .
Уравнение скорости истечения газа с учётом скорости распространения упругих колебаний запишется
v = а × . (41.1 а)
Максимальная скорость истечения при р = 0 будет равна
vmax = а × . (41.2 а)
Поскольку скорость звука является конечной величиной, запишем уравнение энергии для двух сечений, в одном из которых скорость газа равна нулю, а во втором имеет конечное значение v:
+ = . (41.3)
Отсюда следует, что максимально возможная, то есть предельная скорость газа достигается в том случае, если скорость звука в этом сечении равна нулю. Тогда
= , = а0 × . (41.4)
Из уравнения энергии определяем а2:
а2 = – v2 × . (41.3 а)
Отсюда следует, что с увеличение скорости движения газа v, скорость звука убывает. Следовательно, при достаточно большом перепаде давлений в сосуде и окружающей среде может быть достигнуто равенство скоростей потока и скорости звука в этом потоке.
Скорость потока, равная местной скорости звука, называется критической vкр, а соответствующая скорость звука акр.
Скорость движения потока по отношению к скорости распространения упругих колебаний (скорости звука) делится на дозвуковую (v < vкр) и сверхзвуковую (v > vкр). Вводится параметр, который характеризует область движения газа – число Маха М
М = . (41.5)
Это безразмерная скорость, которая показывает, во сколько раз скорость потока больше или меньше скорости звука. М > 1 – сверхзвуковая область движения газа, М < 1 – дозвуковая.
Критическая скорость движения газа при заданной температуре в резервуаре Т1 является постоянной величиной по ходу потока. Поэтому вводят в расчёт критерий скорости – приведенную скорость потока, которая является отношением скорости движения газа в данной точке к критической скорости
L = = . (41.6)
Приведенная скорость вдоль потока является постоянной в отличие от числа Маха.
Тема 42 Течение газа в конфузорах и диффузорах в одномерном приближении (движение газа в трубе переменного сечения)
Для анализа движения газа в каналах с переменным поперечным сечением воспользуемся уравнениями, выражающими закон сохранения массы и закон сохранения энергии. Закон сохранения массы представим в форме уравнения постоянства массового расхода вдоль потока:
Qm = r × v × w = const = C. (42.1)
Закон сохранения энергии используем в виде уравнения Бернулли для идеального газа в дифференциальной форме (пренебрегая величиной dz, то есть полагая dz = 0):
+ v × dv = 0. (42.2)
Продифференцируем по x уравнение неразрывности (42.1):
= ;
r × v × + r × w × + v × w × = 0.
Разделив последнее уравнение на r ´ v ´ w получим:
× + × + × = 0.
Умножив полученное выражение на dx имеем:
+ + = 0. (42.3)
Преобразуем первый член уравнения (42.2), использовав формулу скорости звука а2 = :
= × = а2 × .
Подставим полученное соотношение в уравнение (42.2):
а2 × + v × dv = 0 или = – .
Последнее равенство подставим в уравнение (42.3). Тогда
– + = 0 или = – .
В правой части уравнения вынесем за скобки . Получим
= × .
Обозначим = М – число Маха. Число Маха М – это безразмерная скорость, которая показывает, во сколько раз скорость потока v больше или меньше местной скорости звука а. Окончательно имеем уравнение Гюгонио:
× = . (42.4)
Следствия (анализ) уравнения Гюгонио
1. В дозвуковом потоке (v < а, М < 1) знак dv противоположен знаку dw. То есть при дозвуковом движении газа, так же, как и в случае несжимаемой жидкости, с возрастанием площади сечения трубы скорость движения уменьшается и наоборот.
Рисунок 72
2. В сверхзвуковом потоке (v > а, М > 1) знаки dv и dw одинаковы. Поэтому при уменьшении сечения м скорость движения снижается и наоборот.
Рисунок 73
Это объясняется тем, что произведение r × w из уравнения неразрывности r × v × w = const несмотря на увеличение w всё же уменьшается ввиду резкого уменьшения плотности газа r. И наоборот, произведение r × w увеличивается, несмотря на уменьшение w вследствие резкого увеличения плотности газа r. Если в дозвуковом потоке при изменении сечения трубы плотность газа изменяется незначительно по сравнению со скоростью, то при сверхзвуковом течении газа относительное изменение плотности превосходит по величине относительное изменение скорости. Возрастание скорости, таким образом, связано не только с изменением давления, но и с уменьшением плотности.
3. Если М = 1, то dw = 0 при w ¹ 0. Тогда соответствующее этому случаю сечение w будет критическим. Равенство dw = 0 означает наличие экстремума площади сечения. Причём этот экстремум означает минимальное сечение, так как при подходе к максимальному сечению дозвуковой поток замедляется и не может достигнуть М = 1, а сверхзвуковой ускоряется, что тоже не соответствует М = 1.
4. Если dw = 0 и сечение экстремально (максимальное или минимальное), то либо М = 1 и, следовательно, это сечение критическое, либо М ¹ 1, а dv =0, так как скорость принимает экстремальное значение. При дозвуковом потоке (М < 1) она максимальна в минимальном сечении и наоборот. В сверхзвуковом потоке (М > 1) она максимальна в максимальном сечении и минимальна в минимальном.
На основе анализа уравнения Гюгонио можно предложить способ получения сверхзвукового потока при истечении газа. К выходному сечению конфузорного насадка, в выходном сечении которого скорость газа равна скорости звука (М =1), присоединяют диффузорный насадок. В выходном сечении диффузора скорость газа может быть существенно больше скорости звука в этом сечении. По этому принципу рассчитывается сопло Лаваля.
Рисунок 74 – Сопло Лаваля
Источник
Трудно назвать раздел механики газов, где не использовалось бы в той или иной мере уравнение Бернулли. Познакомимся лишь с некоторыми наиболее важными случаями применения этого уравнения.
Истечение газов через отверстия и насадки
Истечение газов через отверстия и насадки наблюдается при работе горелок, форсунок, при выбивании газа через отверстия в стенах печи и в других случаях. Установим связь между количеством вытекающего газа и размерами отверстия и давлением, под которым происходит истечение. Для простоты возьмем истечение несжимаемого газа, температура которого в процессе истечения практически не изменяется.
Отверстия с острыми краями. Положим, что из сосуда очень больших размеров, давление в котором р1, газ вытекает через отверстие сечением f0 в среду с давлением р2. Для определения скорости истечения газа w2 напишем уравнение Бернулли для сечений I и II (рис. 9). Поскольку температура газа неизменна, постольку hг1 = hг2. В этом случае, пренебрегая потерями, можно написать
(21)
Вследствие большого размера сосуда можно принять w1= 0
Тогда
Отсюда
(22)
В силу инерции частичек истекающего газа сечение струи f меньше сечения отверстия f0. Отношение f/f0= e называется коэффициентом сжатия струи. Скорость w2 фактически относится не ко всему сечению отверстия f0, а лишь к сечению струи f. Для определения расхода газа через отверстие f0 найдем V = w2f. Но f = ef0 следовательно,
(23)
С учетом гидродинамических потерь при истечении через отверстие выражение (23) принимает вид (м3/с)
(24)
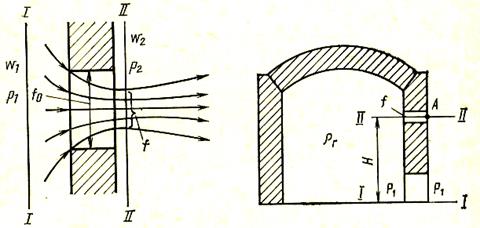
Рис. 9. Истечение газа из отвер- Рис. 10. Истечение из отверстия в
стия в тонкой стенке стечке печи
Смысл коэффициентов j и m, ясен из следующего примера.
Истечение из отверстия в стенке печи (рис. 10) — весьма распространенный на практике случай. Рассмотрим подобный случай истечения (с учетом потерь) из отверстия сечением f, расположенного на высоте Н от уровня пода печи. Напишем уравнение Бернулли для сечения I и точки А в сечении II:
Скорость движения газов в отверстии w2много больше скорости w1; исходя из w2ññ w1, принимаем w1 = 0.
Как следует из изложенного выше, потери на местные сопротивления могут быть определены как
Так как печь сообщается с атмосферой на уровне пода, то статическое давление газа внутри печи и давление воздуха снаружи равны между собой и равны р1.
Давление р2 в точке А соответствует атмосферному давлению на высоте H от уровня сечения I, т. е.
С использованием этих зависимостей уравнение Бернулли принимает вид
или
Отсюда
(25)
Величина учитывает гидравлическое сопротивление отверстия, через которое происходит истечение.
Количество истекающей из рассматриваемого отверстия среды (м3/с) V = w2f2, где f2 — сечение струи, м2.
Но если использовать понятие коэффициента сжатия струи e = f2/f, то
.
Произведение je = m называют коэффициентом расхода.
Истечение через насадки. Насадком называют короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадка обычно составляет 3—4 его диаметра. Количество газа, протекающее через насадок, при прочих равных условиях зависит от формы входных кромок и формы самого насадка. Рассмотрим насадки трех видов, представленные на рис. 11. Пользуясь уравнением (22), получим для них следующие расчетные формулы: для насадки с открытыми кромками
(26)
(27)
Для насадков с закругленными кромками и диффузора
(28)
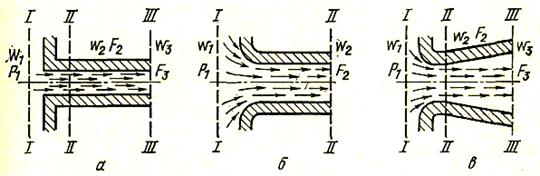
Рис. 11. Истечение газа через цилиндрические насадки:
а — с открытыми кромками; б — с закругленными краями; в — диффузор
Для этих насадков в сечении ІІІ сечения струи и отверстия равны друг другу и поэтому здесь e = 1,0. Сравнение выражений (26), (27) и (28) показывает, что наибольший расход при одинаковом значении р1 — р2и при одинаковом минимальном сечении насадков получается при истечении газа через диффузор, так как площадь выходного сечения у диффузора F3больше, чем у насадков других типов. Угол конусности диффузора не должен превышать 6—7° во избежание отрыва потока от стенок диффузора.
Истечение газов через небольшие отверстия в стенках печи (например, гляделки) можно рассчитывать по формулам для цилиндрического насадка.
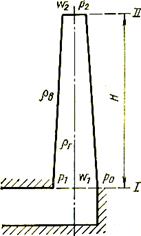Дымовая труба. Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разрежение создается в дымовой трубе благодаря стремлению горячих газов подняться, обусловленному, как будет показано ниже, разностью плотностей холодного наружного воздуха и горячих газов. Найдем зависимость разрежения, создаваемого трубой, от высоты трубы Н и температуры газов. На рис. 12 представлена схема дымовой трубы. За уровень отсчета принимаем сечение ІІ. Напишем уравнение Бернулли в избыточных давлениях для сечений І и ІІ:
hг1 + hст1 + hд1 = hст2 + hд2 + hпот.
Труба в сечении II сообщается с атмосферой, поэтому hст2 = 0. Из приведенного выше уравнения следует, что статическое давление в основании трубы
hст1 = – hг1 + hд2 – hд1 + hпот.
Ввиду незначительных скоростей движения газов в трубе величины потерь, выражаемые в правой части приведенного выше уравнения тремя последними членами, значительно меньше абсолютной величины потери, выражаемой первым членом. Следовательно, статическое давление в основании трубы будет отрицательным, т. е. там будет разрежение. Умножив правую и левую части последнего уравнения на минус единицу, получаем
– hст1 = hраз = hг – (hд2 – hд1) – hпот. (29)
Потери давления в трубе hпот складываются из потерь на трение hтр и потерь, возникающих при выходе газов из трубы в атмосферу и равных xhд2. Учитывая, что коэффициент местного сопротивления на выходе из трубы равен единице (x = 1), можно написать, что
hпот = hтр + hд2.
Вследствие этого уравнению (29) можно придать следующий вид:
hраз = hг + hд1 – 2 hд2 – hтр. (29¢)
Для того чтобы получить окончательное выражение для hразр, в уравнение (29) необходимо подставить все входящие в него величины. Температура газов по высоте дымовой трубы и ее сечение существенно изменяются, поэтому принимаемые в расчете плотность и скорость движения газов в дымовой трубе определяются по средней температуре по высоте трубы. Величина геометрического давления hг, входящего в уравнение (29), выражается уравнением (13). Динамические давления будут соответственно равны
Потери давления на трение находят по уравнению
Подставив в уравнение (29′) значения hг, hд1, hд2, hтр и выразив их через скорости и плотности при нормальных условиях (w0 и r0) по указанным выше выражениям, окончательно получаем (Па)
(30)
где hразр — действительное разрежение в основании дымовой трубы (сечение I), Па; и — плотность соответственно воздуха и газов при нормальных условиях, кг/м3; dср — средний по высоте диаметр трубы, м; w01 и w02 — скорость газов в сечениях I (в основании трубы) и II (в устье трубы) при 0°С, м/с; w0ср — средняя скорость газов по высоте трубы при 0°С, м/с; tв — температура окружающего воздуха, °С; — средняя температура газов по высоте трубы, °С; tг1 и tг2 — температура газов в сечениях I и II, °С.
Если учесть, что
где Т = 273 К,то выражение (30) может быть переписано следующим образом:
Отсюда
(30¢)
В расчетах разрежение в основании дымовой трубы принимают обычно с запасом, равным hразр = 1,3S hпот. Величина S hпот представляет собой суммарные потери напора на пути движения газов от печи до основания дымовой трубы.
При расчете дымовой трубы внутренний диаметр в устье ее dу(на выходе) принимают, исходя из скорости газов, равной 3—10 м/с (при скорости выхода газов, не меньшей 3 м/с, при ветре может происходить их задувание в трубу). Кирпичные и железобетонные дымовые трубы для большей устойчивости делают более широкими в основании. При расчетах внутренний диаметр в основании трубы d0принимают в 1,5 раза больше внутреннего диаметра устья трубы dу, т. е. d0= 1,5dу.
По условиям выполнения кладки dудля кирпичных труб не должен быть меньше 0,8 м.
Падение температуры газов на 1 м высоты трубы принимается для кирпичных и железобетонных 1,0—1,5 °С, а для металлических 3—4°С. Ориентировочно высота трубы может быть определена по уравнению (30) без трех последних его членов.
Подсчитав сумму потерь всех видов на пути движения газов от печи до основания дымовой трубы, по уравнению (30′) находят расчетную высоту трубы Н. Независимо от расчета высота дымовой трубы по правилам сантехники должна быть не менее 16 м и в 2 раза выше самого высокого здания, находящегося в радиусе 100 м вокруг трубы.
Источник