Истечение газа из сосуда

КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Если жидкость или газ находятся в сосуде под давлением, много большим, чем давление, создаваемое весом жидкости, то изменениями давления по высоте столба жидкости можно пренебречь и считать, что истечение подчиняется тем же законам, что и истечение жидкости, находящейся в замкнутом сосуде под давлением pн.Поэтому можно просто определить скорость истечения воды из котла, в котором вода находится под постоянным давлением
пара в несколько десятков атмосфер, или скорость истечения газа из баллона (рис. 292), в котором давление поддерживается постоянным при помощи компрессора. В этих случаях можно считать константу в уравнении Бернулли постоянной по всему объему текущего газа или жидкости и равной рн,давлению в сосуде, так как скоростью течения в сосуде можно пренебречь вследствие того, что сечение сосуда S много больше сечения отверстия s.
Скорость истечения воды из котла будет равна
(105.1)
как легко вычислить из уравнения (102.5).
Для газа уже нельзя определить скорость по формуле (102.5), ибо плотность газа r будет изменяться при движении частицы газа к отверстию. Изменение давления вдоль трубки тока можно при стационарном течении записать по (101.5) так:
(105.2)
Но плотность r теперь уже зависит от величины давления р. При подходе частиц к отверстию давление должно падать: ведь частицы ускоряются в направлении движения. И величина скорости будет зависеть от того, по какому закону изменяется плотность с изменением давления.
Вообще зависимость между давлением и плотностью довольно сложная, так как она связана еще и с изменением температуры вдоль трубки тока. Однако во многих случаях, когда частица движется достаточно быстро, можно считать, как показывает опыт, что давление и плотность связаны законом адиабаты
(105.3)
где c— показатель адиабаты, зависящий от природы газа (для воздуха он равен 1,4), а rн — плотность газа в сосуде. Закон адиабаты (105.3) следует из того, что во время расширения частицы не происходит обмена теплом с окружающими частицами.
Подставим зависимость плотности от давления в (105.2) и, преобразуя, получим
(105.4)
Рис. 292.
Это выражение можно проинтегрировать вдоль линии трубки тока. Если давление в баллоне рн,а давление в пространстве, куда вытекает газ, равно р0,то интегрировать по давлению нужно от рндо р, а по скорости — от нуля до v0— скорости на выходе:
Выполняя интегрирование и преобразуя, получаем скорость истечения:
(105.5)
Если бы мы полагали газ несжимаемым, то из (105.1) получили бы
(105.6)
Скорость истечения газа из баллона под давлением можно записать так:
(105.7)
Теперь легко оценить ошибку, какую допускают при расчетах, в которых газ полагают несжимаемым; для этого нужно только оценить величину корня в (105.7) при данной разности давлений. Можно убедиться непосредственным расчетом, что при очень маленькой разнице в давлениях рни р0,равной, например, нескольким процентам, величина корня будет очень мало отличаться от единицы. Тогда можно рассчитывать скорость и течение газа, как для несжимаемой жидкости.
Определим точнее величину ошибки, которую мы делаем, принимая воздух несжимаемым при давлении, близком к атмосферному. Допустим, что разность давлений в сосуде и вне его составляет 10% от атмосферного, и положим, что давление в сосуде рн равно 1 атм, а вне его р0=0,9 атм. Какова была бы скорость истечения, если бы воздух был несжимаемой жидкостью? Подставляя в (105.6) значение плотности воздуха
и величину атмосферного давления
,
получим
Вычислим теперь значение радикала в (105.7). Обозначим и
(c-1)/c=а, тогда радикал будет иметь такой вид:
разлагаем (1-D)а в ряд Тейлора около единицы и получаем
Подставляя это выражение в радикал и преобразуя, получаем
Подставляя сюда D=0,1 и c=1,4, находим, что ошибка в определении скорости составляет примерно 2%. Следовательно, в тех случаях, когда не нужно высокой точности при определении скорости при разностях давлений, меньших 10% атмосферного, можно пренебречь сжимаемостью воздуха и считать течение воздуха течением несжимаемой жидкости.
Очевидно, что при такой малой разности давлений вдоль трубки тока плотность будет изменяться так же мало; процентное отношение изменений давления и плотности будет примерно тем же. Действительно, при адиабатическом расширении газа на незначительную величину относительное изменение давления будет в c раз больше относительного изменения плотности: ведь из (105.3) получаем dp/p=cdr/r. Небольшое изменение плотности вдоль трубки тока не оказывает влияния на величину скорости, а следовательно, и на характер течения.
Дата добавления: 2015-06-28; Просмотров: 4139; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Рекомендуемые страницы:
Читайте также:
Источник
УДК 536.35
А.М. Гущин1, Н.В. Володарец2, А.П. Соломин3, А.С. Балагура4, Е.А. Бондарь5
1 Донецкий институт железнодорожного транспорта, г. Донецк, Украина,
2 Донецкая академия автомобильного транспорта, г. Донецк, Украина,
3 Донецкий институт железнодорожного транспорта, г. Донецк, Украина,
4 Донецкий институт железнодорожного транспорта, г. Донецк, Украина,
5
Введение.
Истечение газов характеризуется прохождением их через отверстие или короткие патрубки отличающиеся тем, что в процессе прохождения можно пренебречь аэродинамическим сопротивлением и процессами теплообмена.
Процессы истечения на практике используются, для превращения потенциальной энергии давления газа в ёмкости в кинетическую энергию движения газового потока, которая на потоках турбинного колеса превращается во вращающий момент вала этого колеса. Этот процесс осуществляется в системе турбонаддува на тепловозах.
В тех случаях, когда истечение газа происходит из закрытой емкости, в ней снижается давление и температура среды, что приводит к изменению интенсивности процесса истечения.
Постановка задачи.
В термодинамике известна закономерность истечения газов из ёмкости фиксированными значениями температуры и давления газа. При изменяющимся во времени давлении и температуры газов необходимо решать сопряженную задачу собственного истечения газа через патрубок и изменение параметров состояния газа в ёмкости. Процесс истечения газа из ёмкости является гладким. Выделяют две области истечения: закритическое и докритическое. При докритическом истечении интенсивность истечения зависит от параметров состояния газа в ёмкости и давления в среде, в которую происходит истечение. При закретическом истечении интенсивность истечения не зависит от давления в среде истечения. Границей этих двух областей истечения, служит критическое отношение давления в среде истечения и давления в ёмкости из которой происходит истечение
где Рс – давление в среде в которую осуществляется истечение газа;
Ркр – давление газа в ёмкости из которой происходит истечение;
βкр – критическое отношение.
Если значение отношений давлений больше βкр имеет место докритическое отношение, если отношение меньше βкр имеет место закритическое истечение. Значение критического отношения давлений βкр, а так же значения показания адиабаты «К»для разных газов приведено ниже в таблице 1.
Таблица 1
| Атомность газа | Значение показания адиабаты «К» | Критическое отношение давлений βкр |
| Одноатомный | 1.66 | 0.49 |
| Двухатомный | 1.4 | 0.528 |
| Трехатомный и перегретый пар | 1.3 | 0.546 |
В процессе истечения газа из ёмкости происходит снижение давления и его температуры, что неизбежно приводит к появлению теплообмена газа с окружающей средой, а это непосредственно влияет на давление газа в ёмкости и изменению на течение m(кг/с).
Влияние теплообмена на процесс истечения можно учесть двумя способами:
Заданием закона теплообмена или заданием закона изменения параметров состояния газа в ёмкости.
Из изученной литературы об истеченении газа из ёмкости можно выделить четыре задачи:
1. Описание процесса истечения в закритической области при заданности закона соотношения между параметрами состояния газа в ёмкости;
2. Описание процесса истечения в закритической области при заданном законе теплообмена газа в ёмкости с окружающей средой;
3. Описание процесса истечения газа в докритической области при заданном законе соотношения между параметрами газа в ёмкости;
4. Описание процесса истечения газа в докритической области при заданном законе теплообмена газа в ёмкости с окружающей средой.
Цель исследования: Разработать расчетные зависимости для определения изменяющихся во времени давления газа в ёмкости, его температуры, интенсивности истечения.
При решении поставленной задачи использовались известные в термодинамике зависимости:
– уравнение состояния идеального газа для 1-го кг газа и для G кг газа, соответственно:
(1)
где P – давление газа;
– удельный объём газа;
R – удельная газовая постоянная;
T – температура газа;
V – объём ёмкости из которой происходит истечение газа
G – масса газа в объёме V.
– интенсивность истечения газа при фиксированных значениях температуры и давления в закритической области:
(2)
где – коэффициент сопла;
– площадь поперечного выходного сечения сопла;
В качестве заданного соотношения между параметрами газа в ёмкости могут быть соотношения их для изотермического адиабатного или политропного процессов. Политропный процесс можно рассматривать как обобщающий процесс, а два других упомянутых выше можно рассматривать как частные случаи политропного. В связи с этим, соотношение между давлением газа и температурой получается уравнение политропного процесса:
(3)
где n – показатель политропы.
Значение показателя политропы в общем случае может изменятся в широких пределах. Его значение зависит в основном от характера теплообмена газа в ёмкости с окружающей средой. Значение этого показателя находят на практике экспериментальным путём для сходных условий изменения состояния газа.
Находим зависимость описывающую изменение во времени давления газа в ёмкости.
Дифференцируем уравнение (1)
(4)
Члены уравнения (4) разделим на члены уравнения(1), получим:
(5)
Отношение получаем путём дифференцирования уравнения (3)
(6)
Величину dG можно выразить соотношением:
dG=-mdτ (7)
где m – интенсивность истечения (кг/с);
τ – текущее время.
Знак (-) в уравнении (7) поставлен в связи с тем, что массовый расход газа в ёмкости при его истечении уменьшается и его изменение dG должно быть отрицательной величной.
В выражении для m (2) сделаем замену:
(8)
Тогда выражение (7) преобразуется в следующую форму:
(9)
Соотношение в (9) заменим по уравнению (1)
(10)
Значение температуры Т заменим через давление газа Р в соответствии с уравнением (3)
(11)
где Р1 и Т1– начальные значения давления температуры в ёмкости
Соотношение (11) представляем в (9)
; (12)
Текущее значение массы газа в ёмкости выразим из уравнения (1)
(13)
Значение температуры Т в формуле (13) выразим из уравнения (3)
(14)
Соотношение (6), (12) и (14) выразим в уравнении (5)
(15)
После определенных алгебраических преобразований из уравнения (15) получаем:
(16)
Уравнение (16) дифференциальное уравнение с раздельными переменными.
Интегрируем уравнение (16). После интегрирования этого уравнения и некоторых алгебраических преобразований получаем:
(17)
В уравнении (17) выполним замену
(18)
В уравнении (17) преобразуем:
(19)
Таким образом получена зависимость описывающая характер изменения давления в емкости для области закритического истечения для случая, когда соотношение между температурой и давлением газа в емкости соответствует политропному процессу. Изменение температуры во времени найдется из совместного решения уравнений (3) и (19)
(20)
Остаточная масса газа в ёмкости после времени истечения определяется из совместного решения уравнений (13), (19) и (20)
(21)
Интенсивность истечения газа (m) определяется из совместного решения уравнений (2),(8), (11) и (19)
(22)
Формулы (19)…(20) справедливы при истечении до момента когда давление в ёмкости сжимается до критического истечения в соответствии с формулой:
(23)
Из уравнения(19), можно найти время истечения, при котором давление в ёмкости снизится до критического значения. Рассмотрев формулу (19) предположим, что время истечения будет равным:
(24)
Формулы (17)…(24) получены для случая политропного изменения параметров газа в ёмкости. Предположим, что истечение организовано так, что выполнена совершенная теплоизоляция ёмкости. Соотношение между параметрами соотношения в этом случае будет соответствовать уравнению адиабатного процесса. При этом уравнение будут иметь ту же форму, только вместо показателя политропы «n» необходимо подставлять значение показателя адиабаты «К» из таблицы 1.
Далее выведем уравнение изменения во времени давления, интенсивности истечения газа в ёмкости для случая неизменной температуры газа в ней. В качестве исходных используем выше приведенные уравнения (1) и (2)
(25)
Бесконечно малое изменение массы газа в ёмкости вырази через интенсивность истечения «m»
(26)
Интенсивность истечения «m» в соответствиями с формулами (2) и (8) выразится соотношением
(27)
Удельный объём выразим из уравнения (1)
(28)
Тогда значение «m» выразим соотношением
(29)
Соотношение (26) и (29) подставим в (25)
(30)
После интегрирования уравнения (30) получим
(31)
Интенсивность истечения «m» по уравнению (2) с учетом обозначения (8) выразим соотношением:
(32)
Из уравнения (1) находим
(33)
Соотношение (33) подставляем в формулу (32):
(34)
C учетом зависимости (31):
(35)
Из формулы (31) определяем время за которое сначала истечения давления снизится до критического значения. Принимая во внимание соотношение:
(36)
Из уравнения (31) находим искомое время
(37)
Вывод: Приведенные выше результаты исследований позволяют сделать следующие выводы:
1. Показано, что изменение параметров состояния газа в ёмкости определяется не только истечением газа из ёмкости но и неизбежным теплообменом газа в ёмкости с окружающей средой, и для определения зависимостей, описывающих процессы в ёмкости, необходимо выполнить решение спряженной задачи, связывающей процесс истечения с процессом изменения параметров состояния в ёмкость, из которой происходит истечение газа.
2. Изменение параметров состояния газа в ёмкости можно связывать определенными соотношениями имеющими место при адиабатном, изотермическом или политропным процессами или уравнение теплообмена газов в ёмкости с окружающей средой. Закономерность истечения газов иметь две формы: для закритеческого и докритического истечения.
Таким образом, процесс изменения состояния газа в ёмкости распадается на четыре отдельных задачи, отражающие характер истечения газа и характер изменения параметров состояния в ёмкости, из которой происходит истечение газа.
3. Решена задача 1 которая характеризуется истечением в закритической области и заданием политропного, адиабатного и изотермического процесса в ёмкости. Получены зависимости описывающие изменение во времени давления, температуры газа, уравнением интенсивности истечения, количеством остаточного газа в ёмкости, а так же зависимость для определения времени, за которое давление газа снижается до критического значения.
Читайте также:
Рекомендуемые страницы:
©2015-2021 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-11
Нарушение авторских прав и Нарушение персональных данных
Источник
Библиографическое описание:
Курбатов, Е. С. Газодинамика процесса истечения из резервуаров со сжатыми газами / Е. С. Курбатов. — Текст : непосредственный // Молодой ученый. — 2014. — № 8 (67). — С. 49-51. — URL: https://moluch.ru/archive/67/11244/ (дата обращения: 10.01.2021).
В данной статье рассматривается задача истечения сжатого природного газа из ёмкости с высоким давлением в газовую магистраль. В процессе расчетов учитываются два режима истечения — критического и докритического, а также рассматриваются две модели газа — идеального и реального.
Сжатый (компримированный) природный газ (КПГ) сегодня является альтернативой таким видам топлива как пропан, дизель и бензин. Более того, он имеет ряд преимуществ: меньшая токсичность, низкое содержание примесей и т. д. Транспортировка и хранение КПГ осуществляется в баллонах под давлением 25 Мпа при температуре окружающей среды. В случае транспортировки КПГ по воде применяются специальные CNG суда.
Рассматривается задача истечения газа из баллона с давлением = 25 Мпа и объемом =28.872 м3 в газовую магистраль с постоянным давлением = 6.0795 Мпа. Истечение происходит через сопло с площадью поперечного сечения = 0.000785 м2. При уменьшении давлении в баллоне будет наблюдаться сильное понижение температуры внутри самого баллона, следовательно, и его стенок. Стоит задача в нахождении параметров газа: давления, температуры и плотности внутри баллона на всем процессе истечения, а так же самого времени процесса. Рассматриваются две модели газа: идеального и реального.
Сам процесс делится на два режима:
1. Критический. Скорость газового потока эквивалентна скорости звука. Параметры массового расхода и скорости потока газа не зависят от параметра давления .
2. Докритический. Скорость газового потока начинает уменьшаться вплоть до нуля (окончания процесса). Параметры и имеют зависимость от параметра .
Параметр давления находится следующим образом:
Далее следует указать значение . Как известно из газодинамики:
где – показатель адиабаты.
Теперь мы можем определить, в каком режиме находится процесс в данный момент времени. Если параметр принимает значение:
– [0;], то режим истечения критический;
– [;1], то режим истечения докритический.
Для получения параметров давления , температуры и плотности газа используется система из трех уравнений:
 (1)
(1)
где – удельная энтальпия вытекающего газа.
В данной системе, в зависимости от режима, значение массового расхода принимает следующие значения:
– Критический режим:
;
– Докритический режим:
,
где – коэффициент расхода, который учитывает гидравлические потери потока при выходе из сопла; – время окончания процесса.
В задаче рассматриваются две модели газа: идеального и реального. В зависимости от выбранной модели газа в системе (1) уравнением состояния является:
– Уравнение Менделеева — Клапейрона, для случая идеального газа;
где — газовая постоянная;
– Уравнение Редлиха — Квонга, для случая реального газа:
где — постоянные Редлиха — Квонга.
Расчеты проводились численным методом в программе MATLAB. Использовался классический метод Рунге — Кутты четвертого порядка. На рис.1 (модель идеального газа) и рис. 2 (модель реального газа) представлены результаты для параметров давления, температуры и плотности газа. Вертикальная черта на графиках указывает границу перехода от критического режима в докритический.
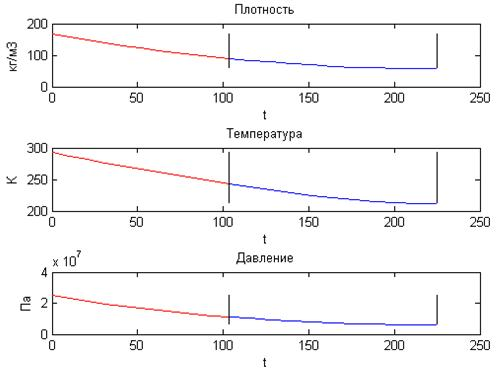
Рис. 1. Параметры идеального газа в баллоне при истечении.
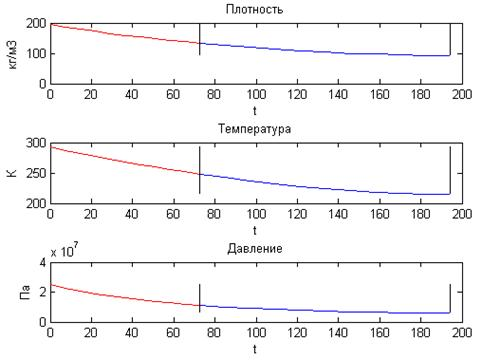
Рис. 2. Параметры реального газа в баллоне при истечении.
Итак, по результатам расчетов можно сделать следующие выводы:
– Время истечения реального газа из баллона составило 194 с.
– Максимально низкая температура в баллоне составляет 215 К и приходится на конец процесса истечения;
– Разница по времени истечения для реального и идеального газа составляет 31 секунду для данной задачи.
Литература:
1. Павловский В. А. Введение в термодинамику реальных газов: Монография ФГУП «Крыловский государственный научный центр». СПб., 2013. 230 с.: ил.
2. Гинзбург И. П. Прикладная гидрогазодинамика. Л.: Издательство ЛГУ. 1958. − 311 с.
3. Павловский В. А., Чистов А. Л. «Моделирование динамики заполнения резервуара реальным газом», СПб., 2013.
4. Вулис Л. А. Теория газовых потоков. М. — Л.: Госэнергоиздат. 1950. − 304 с.
Основные термины (генерируются автоматически): идеальный газ, реальный газ, баллон, модель газа, параметр давления, режим истечения, газовая магистраль, газовый поток, критический режим, массовый расход.
Похожие статьи
Расчёт предпомпажных состояний газотурбинной установки
1. Газогенератора, в котором для создания потока горячих газов высокого давления сжигается смесь из топлива и сжатого воздуха; 2. Силовой турбины, которая служит для преобразования потенциальной энергии газов в кинетическую энергию…
Влияние режимов разработки на характер изменения пластового…
Часто при разработке месторождений природных газов в условиях водонапорного режима давление вначале падает, как при газовом режиме. В дальнейшем увеличение отбора газа и, как следствие…
Дистанционное обнаружение микротрещин в магистральных…
При возникновении утечки из газопровода массовая скорость истечения газа определяется отношением атмосферного давления и давления в трубе.
Массовая скорость звукового истечения газа определяется как: , кг/с. – давление в трубопроводе (Па)
Распределение нейтрального газа в двигателе с анодным слоем
Для оценки распределения газа и параметров потока были вычислены значения всех
Рис. 5. Распределение потока газа в анодном узле.
Так же из-за сильной неравномерности газа происходит повышение давления (рис. 6) в области «запирания», что приведет к пробою [10].
Оценка факторов, определяющих тип главного двигателя…
Часовой расход газового топлива [м3/ч] на режиме определяется по формуле
Для метана эти параметры следующие: критическая температура метана — 190,77 К ( ), критическое давление — 4,626 МПа, критическая плотность 163,5 кг/м3.
Безопасная эксплуатация сетей газопотребления…
Газовая промышленность является одной из самых развитых промышленных отраслей в России.
В случае понижения или повышения давления газа (нормируемого давления газа) в выходном и входном патрубках.
Виртуальная лаборатория для расчета развития топливного факела
Параметры газа оказывают влияние как на процесс истечения топлива из сопла форсунки, так и на дальнейшее поведение
И критический кавитационный параметр (срыва потока).
Коэффициент массового расхода в зависимости от режима рассчитывается по формулам
Исследование диска-крыла в потоке газа, растекающегося от…
Для заданных условий были определены следующие параметры: массовый расход газового потока вытекающего из центровой части аппарата; изменение характеристик обтекания рабочей поверхности ЛА при изменении основных параметров…
Определение расхода воздуха, проходящего через…
В заключение отметим, что формулы (5) — (7), (9) справедливы в области изменения относительного давления « » в пределах от до Параметр называют критическим отношением давлений, при достижении которого расход газа приобретает максимальное значение и…
Источник
