Истечение жидкости из сосуда под давлением

Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ

Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки (коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре, превращается в кинетическую энергию свободной струи.

Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.

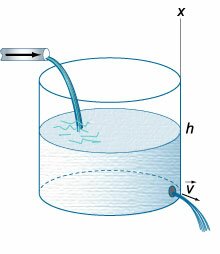
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).

Рис. 5.1. Истечение из резервуара через малое отверстие

Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.

Рис. 5.2. Истечение через круглое отверстие

Степень сжатия оценивается коэффициентом сжатия.

где Sс и Sо – площади поперечного сечения струи и отверстия соответственно; dс и dо – диаметры струи и отверстия соответственно.

Скорость истечения жидкости через отверстие такое отверстие

где Н – напор жидкости, определяется как

φ- коэффициент скорости

где α – коэффициент Кориолиса;

ζ- коэффициент сопротивления отверстия.

Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:

Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.

В итоге получаем расход

где ΔР – расчетная разность давлений, под действием которой происходит истечение.

При помощи этого выражения решается основная задача – определяется расход.

Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости

где ν – кинематическая вязкость.

При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.

Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).

Рис. 5.5. Схема несовершенного сжатия струи

Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в п.5.1.

При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной Н.Е. Жуковским:

где n – отношение площади отверстия Sо к площади поперечного сечения резервуара S1

Расход жидкости при несовершенном сжатии

где напор Н нужно находить с учетом скоростного напора в резервуаре

Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное отверстие.

Рис. 5.6. Истечение по уровень

В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.

Скорость истечения в сжатом сечении струи

где φ – коэффициент скорости;

Н – расчетный напор,

Расход жидкости равен

Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.

Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.

Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.

Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис.5.7).

Рис. 5.7. Истечение через насадок

Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:

Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.

Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка

P2 – P1 0,75Hgρ

При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому

Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.5.8).

Рис. 5.8. Второй режим истечения через насадок

Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.

При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.

Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.

Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих коэффициентов.

Рис. 5.9. Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся конические; в – коноидальные; г – внутренние цилиндрические

Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.

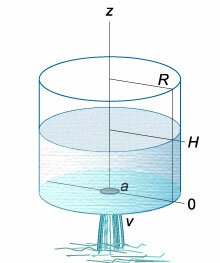
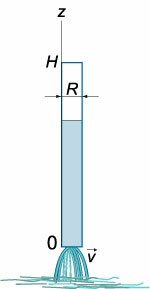
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).

Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.

Рис. 5.10. Схема опорожнения резервуара

Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровнеS, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

где dh – изменение уровня жидкости за время dt.

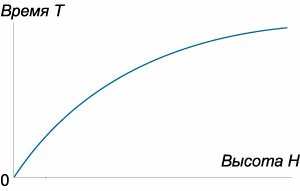
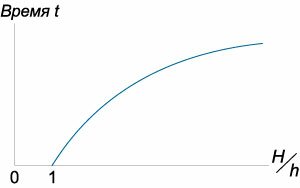
Отсюда время полного опорожнения сосуда высотой Н

Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения

Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

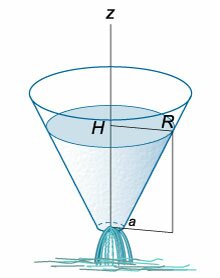
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:

где l – длина цистерны; D – диаметр цистерны.

Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным

Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия, перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения, истечение из которых и рассмотрим.

Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором влияет на истечение.

Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением (рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды (рис. 5.14).

Рис. 5.13. Истечение из-под затвора через незатопленное отверстие

Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости. На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей зависимостью:

hc = ε’a

где ε’ – коэффициент вертикального сжатия струи.

Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать ε’ = 0,64.

Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после преобразований получим:

где φ – коэффициент скорости,

где Н0 – напор с учетом скорости подхода,

Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:

где S – площадь отверстия, S = ab.

Рис. 5.14. Истечение из-под затвора при затопленном отверстии

При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:

где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под затвора струи.

Глубина hz определяется из зависимости

в которой

а hб – глубина в отводящем канале (бытовая глубина).

Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку, имеет вид

На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и уравнения, по которым вычисляется давление струи на соответствующую поверхность.

Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).

В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения. В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец, в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.

Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью

Рис. 5.16. Составные части свободной струи

Источник

    Истечение жидкости через насадки, из отверстий и через водосливы. Насадки широко применяют на нефтегазоперерабатывающих заводах в различных устройствах. Примером цилиндрических насадков являются дренажные трубы резервуаров, емкостей и технологических аппаратов. Конические сходящиеся насадки используют для получения больших выходных скоростей и увеличения дальности полета струи в приборах пожаротушения, соплах турбин, в форсунках и горелках, Расходящиеся конические насадки служат для замедления скорости движения жидкости и увеличения давления в эжекторах, на выходе центробежных насосов и т. п. Насадки различных типов применяют в градирнях, ректификационных и других колоннах для диспергирования жидкости, в контрольноизмерительных приборах для управления потоками воздуха, в водоструйных насосах и т. д. [c.55]

    Р – давление, при котором происходило истечение жидкости т-время истечения жидкости в объеме V  [c.249]

    Разрушение пен связывают, главным образом, с капиллярным давлением, обусловливающим переток жидкости в утолщенные участки, которые находятся под меньшим гидростатическим давлением (жидкость в утолщениях пленки имеет вогнутые мениски), а также с диффузией газа из малого пузырька в более крупный через пленку, разделяющую их. При разрушении пены может преобладать тот или иной процесс в зависимости от природы и состояния пены. В пенах с толстыми жидкими прослойками сначала происходит истечение жидкости, приводящее к утончению пленок, а затем диффузия газа и разрыв пленок. Разрушение пен высокой кратности ( сухих ) обусловлено в основном диффузней газа и прорывом пленок. [c.350]

    Для измерения кинематической вязкости применяют наборы капиллярных стеклянных вискозиметров типов ВПЖ-1, ВПЖ-2, ВНЖ, выпускаемых по ГОСТ 10028. Вискозиметры типа ВПЖ-1 применяются для измерений вязкости прозрачных (просвечивающихся) нефтепродуктов при температурах выше О °С. Они являются наиболее точными из капиллярных вискозиметров, так как конструкция предусматривает образование “висячего уровня” при течении жидкости, тем самым время течения жидкости не зависит от гидростатического давления и количества жидкости, налитой в вискозиметр. Вискозиметры типа ВПЖ-2 применяют для измерений вязкости прозрачных (просвечивающихся) нефтепродуктов как при положительных, так и при отрицательных температурах. Вискозиметры типа ВНЖ используют для измерений вязкости непрозрачных жидкостей, какими чаще всего являются нефти. В отличие от первых двух типов в вискозиметрах типа ВНЖ производятся измерения не времени истечения жидкости по капилляру, а измерения времени заполнения жидкостью приемного резервуара вискозиметра. Это вискозиметры обратного тока. В паспорте на вискозиметры типа ВНЖ даются две калибровочные постоянные, соответствующие заполнению вискозиметра жидкостью до первой и второй риски, расположенной на трубке вискозиметра. [c.247]

    Истечение жидкости под давлением [c.58]

    Истечение жидкости из закрытого сосуда может происходить под действием давления сжатого воздуха на поверхность жидкости, [c.58]

    Скорость истечения жидкости под давлением зависит от разности давлений ро – Рх, высоты подъема 21 – 2о и сопротивлений в трубопроводе 1о, х. [c.58]

    При выдавливании (экструзии) пластичных жидкостей применяется червячный (винтовой) пресс. Подающий винт проталкивает жидкость в камеру с профилированным отверстием. В камере образуется некоторое избыточное давление Др, вызывающее истечение жидкости из отверстия с определенной скоростью. Между витками подающего винта жидкость передвигается потоком высотою Л и щириною Ь. На поверхности вала винта жидкость вращается вместе с ним, следовательно, составляющая скорости жидкости по спиральной линии здесь равна нулю. У стенки аппарата жидкость передвигается с наибольшей скоростью. Таким образом, если окружная скорость по спиральной линии (составляю- [c.170]

    Истечение жидкости из отверстия в боковой стенке. При постоянных значениях давления ро над уровнем жидкости в сосу де и высоты 2о расположения этого уровня относительно плос- [c.130]

    Если из сосуда постоянного сечения шо м , в котором давление над уровнем жидкости равно ро н/м” , происходит истечение из отверстия сечением и в пространство, где давление также равно ро, то время истечения жидкости определяется уравнением [c.131]

    При испытаниях образцов под действием переменного во времени давления и силы вместо постоянных грузов используется бак с жидкостью. При истечении жидкости из бака с определенным расходом в образце создается соответствующее переменное усилие или давление. [c.104]

    Исследованные штуцера (рис. 1) устанавливались в конце трубы. К штуцеру подавалась чистая жидкость. Давление перед штуцером фиксировалось по уровню манометрической трубки. Истечение происходило в атмосферу. [c.89]

    Процедура измерения сводится к регистрации времени I истечения исследуемой жидкости из резервуара 1 вместимостью V от метки А до метки В. Напряжение деформации т регулируется путем соединения штуцера 4 с маностатом, в котором создается определенное давление газа (воздуха) Р . В простейшем случае (при исследовании заведомо ньютоновской жидкости) истечение жидкости происходит под действием гидростатического давления Рг = РЁ > где р-плотность исследуемого раствора -ускорение силы тяжести Н- средняя разность уровней раствора в резервуарах / и 2. В общем случае напряжение определяется суммарным давлением Р = Р 4-Яг- [c.220]

    Ламинарное течение жидкости описывается законом Пуазейля скорость истечения жидкости через капилляр пропорциональна приложенному давлению и обратно пропорциональна вязкости  [c.430]

    Истечение жидкости происходит под давлением столба жидкости Ь в вискозиметре р = рф, тогда формула (50) может быть представл ена в виде [c.50]

    Установка для определения зависимости скорости истечения жидкости от давления с вискозиметром Уббелоде. [c.131]

    Установка для определения зависимости скорости истечения жидкости от давления схематически изображена на рис. У.4. Вакуум в установке создается [c.131]

    Необходимым условием использования уравнения Пуазейля для расчета вязкости является ламинарность движения жидкости в капилляре. Турбулентности потока избегают путем соответствующего подбора диаметра и длины капилляра вискозиметра. В вискозиметрах, применяемых для определения вязкости растворов полимеров, условия течения жидкости в капилляре при обычных перепадах давления соответствуют числам Рейнольдса, меньшим 200. Отклонения от закона Пуазейля возможны также вследствие того, что, строго говоря, растворы полимеров представляют собой неньютоновские жидкости, вязкость которых зависит от скорости их истечения через капилляр. Для того чтобы свести к минимуму этот источник ошибок, для измерений вязкости растворов полимеров принято использовать вискозиметры, время истечения жидкости в которых достаточно велико и составляет 100-200 с. [c.140]

    Структурированные системы ие подчиняются законам Пуазейля и Ньютона. Вычисленная по соответствующему уравнению вязкость таких систем имеет переменное значение и является функцией градиента скорости. У таких систем чем выше давление, под которым происходит истечение жидкости по капилляру (т. е. чем больше скорость истечения), тем ниже величина вязкости, найденная опытным путем. [c.382]

    В подготовленных таким образом для испытания вискозиметрах жидкость под давлением собственного веса начнет протекать из колена 1 через капилляр в колено 2. Точно в тот момент, когда уровень жидкости достигнет метки включают секундомер и останавливают его точно в тот момент, когда уровень жидкости достигнет метки Ма- Время, отмеченное по секундомеру, записывают. Определение времени истечения жидкости через капилляр повторяют несколько раз. Число параллельных замеров, согласно ГОСТ 33-66, устанавливается в зависимости от времени истечения пять измерений при времени истечения от 200 до 300 сек четыре – при времени истечения от 300 до 600 сек три – при времени истечения свыше 600 сек. [c.187]

    С явлением капиллярности приходится сталкиваться при использовании стеклянных трубок в приборах для измерения давления, а также в некоторых случаях истечения жидкости. Большую роль приобретают силы поверхностного натяжения в жидкости, находящейся в условиях невесомости. [c.11]

    Пусть истечение жидкости происходит под действием давления /)(, в среду газа с давлением р – Расчетный напор при совершенном сжатии в этом случае [c.131]

    Точка пересечения кривой потребного напора с осью абсцисс при Az = А2 собой расход при движении жидкости самотеком, т. 0. за счет лишь разности нивелирных высот Az. Потребный напор в этом случае ранен нулю, так как давление в начале и в конце трубопровода равно атмосферному (за начало трубопровода считаем свободную поверхность в верхнем резервуаре) такой трубопровод условимся называть самотечным (рис. 1.97). Если в конце самотечного трубопровода происходит истечение жидкости в атмосферу, то в уравнении (1.138) для потребного напора к потерям напора следует добавить скоростной напор. [c.139]

    Двухкаскадный гидроусилитель (рис. 3.95,6, см. также рис. 3.67) имеет первую ступень усиления в виде вспомогательного устройства тина сопло-заслонка 2 (или иного типа), которое обычно приводится электромагнитом 1. При изменении положения заслонки 2 увеличивается сопротивление истечению жидкости из соответствующего сопла 5, в результате чего в соответствующей полости золотника повысится давление, нод действием которого плунжер, преодолев усилие пружины 5, сместится в соответствующее положение. [c.466]

    На рис. 2.16 представлена зависимость йд = Лд(аУо, Я) в возможном диапазоне изменения скорости истечения жидкости Шо (начальной скорости капель) и радиуса капли Я для струи диспергированной жидкости из центробежной форсунки при умеренных давлениях распыла. Видно, что лишь крупные капли при относительно высоких скоростях испытывают заметную деформацию. Количество [c.126]

    После газонасыщения участок трубопровода, содержащий имитируемый разрыв, отсекался линейными задвижками, насос отключался. Длина отсекаемого участка в различных опытах могла изменяться. Мгновенным открытием газового крана, пропускное сечение которого значительно больше площади отверстия в теле трубы, начинался процесс опорожнения отсеченного участка трубопровода. При истечении жидкости регистрировались давление самопишущим манометром МТС-71-1, температура жидкости терморезистором МТТ-4 с вторичным прибором и количество вытекающей жидкости в мерную емкость, снабженную датчиком поверхности уровня. [c.138]

    Произведенные выше расчеты относятся к корзинкам центрофуг без отверстий. При наличии последних вогфос сильно усложняется по двум причинам. Во-первых, фактическое давление на стенки будет, очевидно, значительно ниже вычисленных по приведенным формулам, так как в отверстиях, где происходит истечение жидкости, давление резко падает, и действительная картина распределения давлений по стенке будет весьма сложной. С другой стороны, наличие отверстий влечет за собой, [c.322]

    Исследование процесса образования пузырей и капель при истечении жидкостей или газов из отверстий и сопел имеет исключительно важное значение для разработки научно-обоснованных методов расчета колонных аппаратов, в которых межфазная поверхность создается путем диспергирования жидкости или газа. Механизм образования пузырей и капель чрезвычайно спожен и определяется очень большим числом параметров. Параметры, влияющие на процесс образования пузырей, можно подразделить на конструктивные, параметры, связанные со свойствами газов и жидкостей, и режимные параметры. К первому классу относятся диаметр, форма, ориентация и конструкция сопла, а также материал, из которого он изготовлен. Кроме того, чрезвьиайно важным конструктивным параметром для образования пузырей, является объем газовой камеры, из которой происходит йстечение газа в жидкость. К параметрам, связанным со свойствами выбранной системы, можно отнести поверхностное натяжение на границе раздела фаз, плотность и вязкость жидкости и газа, угол смачивания и скорость звука в газе. И, наконец, режимные параметры включают объемный расход диспергируемой фазы, величину и направление скорости сплошной фазы, высоту уровня жидкости в колонне, перепад давления в сопле и температуру. Не все названные параметры равноценны и одинаково важны для процессов образования капель и пузырей, однако большинство оказывает существенное влияние на величину отрывного диаметра и частоту образования диспергируемых частиц. [c.48]

    Расчет гидравлического сопротивления аппаратов цилиндрической формы [45]. Удельные потери, т. е. потери давления на единицу тол[цины слоевого (пористого) цилиндра при данном расходе жидкости меняются с Т0ЛН1.ИН0Й стенок цилиндра. При истечении жидкост[[ наружу скорость в направлении истечения падает вместе с увеличением поверхности (диаметра) цилиндрического слоя, а следовательно, удельные потери у.мень-шаются. При всасывании имеет место обратное явление. Если использовать известные формулы, цля коэффициентов сопротивления илоских слоев, то это обстоятельство должно быть учтено. Сделаем соответствующие пересчеты. [c.306]

    Истечение из донного отверстия при постоянном уровне. Рассмотрим истечение жидкости из сосуда, имеющего отверстие в нижнем днище, при постоянном уровне жидкости в сосуде Н == = onst (рис. И-13). На поверхность жидкости в сечении 1-I действует давление Жидкость истекает в окружающую среду, в которой действует давление р. – В случае идеальной жидкости уравнение Бернулли, записанное для сечений 1-1 и 2-2, будет иметь вид [c.55]

    Истечение из отверстия в дне сосуда при постоянном напоре. На рис.4.11 представлен сосуд с отверстием в горизонтальнои дне, через которое вытекает жидкость. Давление над уровнем жидкости в сосуде ран/м , давление среды, в которую происхс-дит истечение, рн/м . Расстояние от произвольно взятой плоскости сравнения х-х до уровня а-Ь жидкости в сосуде – го л. то же до сечения с-с( иа уровне отверстия – г м. [c.128]

    Значения т, оцененные из геометрических характеристик капилляра, а также перепада давления АР в процессе течения, должны быть скорректированы на так называемые входовые эффекты . Дело в том, что истечение жидкости из вискозимефического [c.168]

    К а п и л л я р н ы метод состоит в определении объема V в сж жидкости, протекающей под давлением р (в динах на 1 см ) в течение времени I сек, через капиллярную трубку длиной I и радиусом г. Пуазель показал, что при ламинарном истечении жидкости через капилляр зависимость между указанными величинами определяется уравнением [c.68]

    Устройство вискозиметра Уббелоде и установки для определения скорости истечеиия. Вискозиметр Уббелоде представляет собой и-образпую стеклянную трубку, п каждом колене которой имеются небольшие ])езервуары (шарики) одинакового размера, расположенные па одном уровне. Над одним шариком обычно находится баллончик, служащий ловушкой, предотвращающий выброс жидкости из вискозиметра. Под другим шариком находится капилляр, нерез который жидкость под действием создаваемого вакуума перетекает из одного шарика в другой. Такое устройство вискозиметра позволяет не принимать в расчет действие силы тяжести и считать, что истечение жидкости происходит только под влиянием перепада давлений в обоих коленах вискозиметра. [c.131]

    Вычислить скорость истечения жидкости из капил-ляра длиной / = 5-10-2 радиусом сечения г = = 25-10-5 Л1 под давлением р= 980 н1м . Вязкость жидкости т] =2-10-3 ц-сек1м . [c.48]

    Весь процесс истечения через разрыв можно разбить на три последовательно протекающих режима упругий, газоупругий и режим истечения свободного газа. Особенно наглядно это видно из графика (рис. 48), где представлен характер изменения давления в зависимости от времени истечения через разрыв, расположенный в пониженных местах профиля трассы трубопровода. Кривые АВ1, АВ2, АВз соответствуют упругому режиму, в котором истечение жидкости происходит только за счет упругих свойств [c.139]

Источник