Истечение жидкости из закрытого сосуда

ЛЕКЦИЯ 7 УРАВНЕНИЕ БЕРНУЛЛИ И ЕГО СЛЕДСТВИЯ
1. Линии тока и трубка тока. Условие неразрывности струи.
2. Уравнение Бернулли.
3. Следствия уравнения Бернулли.
4. Принцип работы инжектора, ингалятора.
5. Основные понятия и формулы.
6. Задачи.
7.1. Линии тока и трубка тока. Условие неразрывности струи
Течение жидкости изображается линиями тока –
линиями, касательные к которым в каждой точке совпадают с направлением
вектора скорости частиц. Течение жидкости называется установившимся, стационарным, если
скорости частиц в каждой точке потока со временем не изменяются (при
этом условии линии тока совпадают с траекториями частиц жидкости).
При стационарном течении линии тока остаются неизменными. Часть потока жидкости, ограниченная линиями тока, образует трубку тока. Частицы
жидкости не выходят за пределы трубки тока, поэтому через любое ее
сечение проходит одно и то же количество жидкости. Объем Q жидкости,
протекающей за единицу времени через любое сечение S, перпендикулярное
оси трубки тока, определяется формулой
где v – скорость движения частиц жидкости в данном сечении.
Для
идеальной жидкости, не подверженной действию сил трения, скорости
движения частиц во всех точках одного и того же поперечного сечения
трубы одинаковы. Эта общая скорость и входит в уравнение (7.1).
На частицы реальной жидкости действуют силы трения со стороны стенок трубы и со стороны соседних частиц. Поэтому скорость
частиц
жидкости в поперечном сечении трубы различна: она максимальна в центре
трубы и уменьшается до нуля у ее стенок. В этом случае в формуле (7.1) v – это средняя скорость течения жидкости в данном сечении.
Условие неразрывности струи: при
стационарном течении несжимаемой жидкости через любые сечения трубки
тока каждую секунду протекают одинаковые объемы жидкости, равные
произведению площади сечения на среднюю скорость движения ее частиц.
Уравнение (7.1) выражает условие неразрывности струи. Оно устанавливает соотношение между скоростями течения жидкости в различных сечениях трубки тока:
Если
жидкость движется по трубе переменного сечения, то скорость ее движения
обратно пропорциональна площади сечения трубок (рис. 7.1).
Рис. 7.1. Движение жидкости в трубе с разными сечениями. Длина стрелок изображает среднюю скорость течения жидкости
Площадь сечения пропорциональна квадрату диаметра трубки (S = πd2/4), поэтому если диаметр трубки в сечении С вдвое меньше,
чем в сечении А, то площадь поперечного сечения С в четыре раза меньше,
чем площадь сечения А. Следовательно, и скорость потока в сечении С
будет в четыре раза больше, чем в сечении А.
Уравнение неразрывности струи при протекании крови в сосудах
Кровеносная
система человека – это сложная замкнутая система эластичных трубок
разного диаметра. В нее входят: аорта, артерии, артериолы, капилляры,
венулы, вены. Из сердца кровь поступает в аорту, а оттуда распределяется
по главным артериям, затем по
более мелким и в конце
концов расходится по миллионам мелких капилляров. По венам кровь
возвращается в сердце. (Один цикл движения крови длится в среднем 20 с.
За сутки сердце перегоняет по всем сосудам до 10 000 л крови!) Скорость
кровотока в разных сосудах различна. Ориентировочные значения этой
скорости представлены в табл. 7.1.
Таблица 7.1. Скорость и давление крови в различных сосудах
На
первый взгляд кажется, что приведенные значения противоречат уравнению
неразрывности – в тонких капиллярах скорость кровотока примерно в 1000
меньше, чем в артериях. Однако это несоответствие кажущееся. Дело в том,
что в табл. 7.1 приведен диаметр одного сосуда. Эта величина
действительно уменьшается по мере разветвления. Однако суммарная площадь
разветвления возрастает. Так, суммарная площадь всех капилляров (около
2000 см2) в сотни раз превышает площадь аорты – этим и
объясняется такая малая скорость крови в капиллярах. Малая скорость
кровотока в капиллярах необходима для обеспечения эффективного обмена
между кровью и тканями.
7.2. Уравнение Бернулли
Для
идеальной жидкости (сила трения полностью отсутствует) справедливо
уравнение, которое было получено швейцарским математиком и физиком
Даниилом Бернулли (1700-1782). Рассмотрим тонкую трубку тока и выделим в
ней два произвольных сечения (рис. 7.2).
Рис. 7.2. Параметры сечений в трубке тока
В общем случае эти сечения находятся на различных высотах (h1 и h2), а их площади различны (S1 и S2). Вследствие уравнения неразрывности различны будут и скорости течения жидкости в этих сечениях (v1и v2). Обозначим давления жидкости в этих сечениях Р1 и Р2 соответственно.
Используя закон сохранения механической энергии, можно доказать, что для этих сечений выполняется следующее соотношение:
Давление Р называют статическим. Это
давление, которое оказывают друг на друга соседние слои жидкости. Его
можно измерить манометром, который движется вместе с жидкостью. Величину
ρv2/2 называют динамическим давлением. Оно обусловлено движением жидкости. Гидростатическое давление ρgh – это давление, создаваемое весом вертикального столба жидкости высотой h.
Уравнение Бернулли формулируется следующим образом:
При
стационарном течении идеальной жидкости полное давление, равное сумме
статического, динамического и гидростатического давлений, одинаково во
всех поперечных сечениях трубки тока.
7.3. Следствия уравнения Бернулли
Горизонтальная трубка тока переменного сечения
При этом h1 = h2 и уравнение (7.3.) принимает вид
Отсюда
следует, что статическое давление идеальной жидкости при течении по
горизонтальной трубке возрастает там, где скорость ее уменьшается, и
наоборот. Это можно продемонстрировать с помощью манометрических трубок,
уровень поднятия жидкости в которых пропорционален статическому
давлению (рис. 7.3). Видно, что в широком сечении (а), где скорость
течения меньше, статическое давление больше, чем в узком сечении (б).
Наклонная трубка тока постоянного сечения
В такой трубке скорость жидкости везде одинакова (v = const), и уравнение (7.3) принимает вид
Следовательно,
скорость истечения струи равна скорости тела при свободном падении с
высоты h. Соотношение (7.9) – это формула Торричелли.
Рис. 7.3. Горизонтальная трубка переменного сечения
Рис. 7.4. Наклонная труба постоянного сечения
Рис. 7.5. Линия тока при истечении жидкости из небольшого отверстия широкого сосуда
Измерение скорости жидкости
Установим
в разных местах горизонтальной цилиндрической трубы (струи жидкости)
одного сечения две трубки: 1) манометрическую трубку, плоскость
отверстия которой расположена параллельно движению жидкости; 2) трубку,
изогнутую под прямым углом навстречу движению жидкости (трубку Пито)
(рис. 7.6).
В движущемся потоке жидкость в трубках
поднимается на разную высоту. Давление под манометрической трубкой равно
статическому давлению Р. Оно уравновешивается давлением атмосферы Ра и давлением столба жидкости h2:
Имея систему двух таких трубок, вычисляют скорость потока жидкости по формуле (7.10).
Рис. 7.6. Измерение скорости жидкости
7.4. Принцип работы инжектора, ингалятора
В
медицине широкое применение находят приборы, действие которых основано
на использовании законов гидродинамики. Рассмотрим два таких прибора.
Инжектор
Этот
прибор используют для дозированной подачи пациенту газообразного
препарата. Например, закиси азота или кислорода. Препарат из баллона
поступает в смесительную камеру через узкое сопло (рис. 7.7).
При
этом скорость движения препарата возрастает, а его давление, в
соответствии с уравнением Бернулли, падает. В смесительной камере
возникает разрежение, и в нее засасывается атмосферный воздух.
Всасывание происходит через одно из отверстий поворотного диска.
Отверстия имеют различные диаметры. Выбирая соответствующее отверстие,
регулируют состав смеси, подаваемой пациенту.
Рис. 7.7. Подача кислорода при кислородной терапии
Ингалятор
Этот прибор используют для введения в область носоглотки лекарственных средств в распыленном виде (рис. 7.8).
Рис. 7.8. Схема ингалятора
Он состоит из двух трубок, расположенных под прямым углом.
Горизонтально
расположенная трубка (1) имеет на конце сужение. Чуть ниже этого конца
располагается верхний конец вертикальной трубки (2), нижний конец
которой опущен в сосуд с жидким препаратом. В горизонтальную трубку
подается пар (3). При прохождении суженного конца скорость пара
возрастает, а давление падает. В область пониженного давления
засасывается препарат, который распыляется струей пара. В результате
образуется смесь пара, воздуха и капелек препарата, которая через
патрубок (4) поступает к пациенту.
7.5. Основные понятия и формулы
Продолжение таблицы
7.6. Задачи
2. Кровь
течет по горизонтальному участку артерии, имеющему сужение. Где
давление крови на стенки сосуда будет больше – на суженном или широком
участке? Динамическим или статическим давлением обусловлено
фонтанирование крови при надрезе артерии?
Решение
Фонтанирование крови при надрезе артерии обусловлено разностью между статическим давлением в артерии и давлением атмосферы.
При
прохождении места сужения скорость кровотока возрастает (7.2), а
статическое давление, которое и воздействует на стенки сосуда,
уменьшается (7.5). Отметим, что вклад динамического давления в полное
давление ничтожен. Действительно, принимая v = 0,5 м/с, ρ = 103 кг/м3, найдем:
Ответ: давление
на стенки незначительно уменьшается на участке сужения артерии.
Фонтанирование крови при надрезе артерии обусловлено статическим
давлением.
3. Скорость потока крови в капиллярах равна примерно v1= 30 мм/мин, а скорость потока крови в аорте v2= 45 см/с. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты.
4. Лекарственный раствор вводят в мышцу животного с помощью шприца, внутренний диаметр которого d1 = 10 мм, а диаметр иглы d2 = 0,5 мм. Определить скорость истечения раствора из иглы, если скорость перемещения поршня шприца равна v1 = 2,3 см/с.
7. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость течения крови: v1= 0,5 мм/с. Средняя скорость тока крови в аорте составляет v2=
40 см/с. На основании этих данных определить, во сколько раз суммарная
площадь поперечных сечений функционирующих капилляров больше площади
сечения аорты.
Решение
Условие
неразрывности струи было получено для трубки тока переменного сечения.
Очевидно, что оно применимо и к разветвлению труб. В задаче такое
разветвление начинается с аорты (площадь поперечного сечения S2) и заканчивается капиллярами (общая площадь сечения S1). Исходя из этого запишем уравнение неразрывности струи (7.2): S1/S2 = v2/v1= 800.
Ответ: 800.
8. При
всасывании человек может понизить давление в легких на 80 мм рт.ст.
ниже атмосферного. Определить, на какую высоту ему удастся втянуть воду
по трубочке.
10. Во время бури или смерча с домов иногда срывает крыши. Используя уравнение Бернулли, объяснить, почему это происходит. Решение
Давление в потоке ветра уменьшается. Поэтому давление на чердаке превышает внешнее давление на величину ΔΡ = pv2/2. При этом на кровлю действует направленная наружу сила F = Spv2/2. При скорости v = 35 м/с (ураган), ρ = 1,3 кг/м3 и S = 100 м2 величина силы составляет F = 61 000 Н (6 т), что существенно превышает вес кровли.
Источник
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
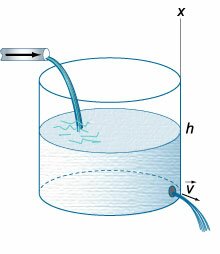
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
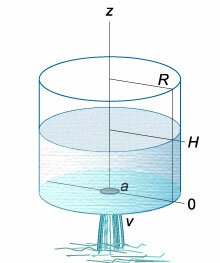
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
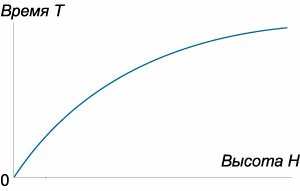
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
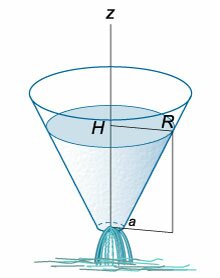
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
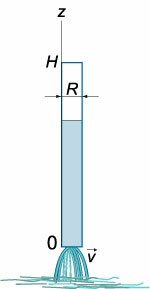
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
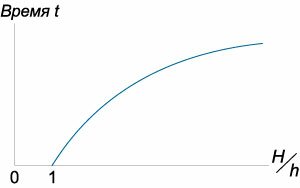
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник