Из одного сосуда в другой по трубке
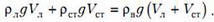
Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Задача по физике – 4953
В цилиндре, заполненном жидкостью, имеется поршень, форма которого изображена на рисунке. Слева на поршень действует некоторая сила. Так как справа площадь поршня больше, чем слева, то можно ожидать большую силу давления на воду. А раз так, то можно как будто получить и большую работу при некотором перемещении поршня влево. В чем ошибка таких рассуждений?
Подробнее
Задача по физике – 4954
В одинаковых сообщающихся сосудах А и В находится комнатная вода (рис.). Кран К закрыли и воду в сосуде В нагрели, вследствие чего ее уровень немного повысился’. Станет ли вода переливаться из одного сосуда в другой, если открыть кран?
Решение. Один ученик сказал, что увеличение высоты столба жидкости в сосуде В вызовет увеличение давления на уровне соединительной трубки. Поэтому жидкость будет перетекать из сосуда В в сосуд А, если открыть кран /С.
Другой ученик утверждал, что после нагревания воды в сосуде В давление в обоих сосудах не изменилось, так как не изменились вес воды и площадь основания дна сосуда.
Третий ученик доказывал, что давление воды в сосуде В на уровне соединительной трубки после ее нагревания уменьшится. И если открыть кран К, то вода будет перетекать из сосуда А в сосуд В. Это происходит потому, что сосуд В расширяется кверху, и увеличение высоты уровня воды в нем не будет обратно пропорционально уменьшению плотности, вызванному нагреванием воды. Кто же из учеников прав?

Подробнее
Задача по физике – 4955
Большая круглая железная труба, изогнутая в виде кольца с просветом между точками А и В (рис.), наполовину закапывается в землю и наполовину висит над землей. Мельничное колесо, состоящее из ряда лопаток, насаженных на ось, помещается внутри подземной части трубы в точке В. Если в эту трубу, в левую ее половину, возле точки В сразу вылить 2—3 бочки воды, то (по мнению автора проекта) эта вода с разгона помчится по трубе, дойдет до точки А, снова обрушится вниз и т. д., попутно приводя мельничное колесо в быстрое вращательное движение. Единственное, что якобы необходимо для дальнейшей бесперебойной работы мельницы,— это время от времени подливать в трубу воду для замены той, которая испарилась. В чем ошибка проекта? Как фактически стала бы двигаться вода в трубе?

Подробнее
Задача по физике – 4956
Полный стакан с водой, взятой при температуре $20^{ circ} C$, накрывают листом бумаги и, придерживая лист, переворачивают стакан. Затем убирают руку, которая придерживала лист. Вода не выливается. Ее удерживает атмосферное давление.
Повторим тот же опыт без листа бумаги. Вода выливается из стакана. Но ведь атмосферное давление существовало и в этом случае, а результат получился другой. Как объяснить этот парадокс?
Подробнее
Задача по физике – 4957
К чашке равноплечих весов подвешена тонкостенная цилиндрическая барометрическая трубка со ртутью (рис.). Конец трубки лишь на ничтожную глубину погружен в чашку со ртутью. Чтобы уравновесить весы, надо на другую чашку весов поместить груз, вес которого равен сумме весов трубки и ртутного столба в ней.
Но ведь ртуть в трубке (если пренебречь трением ртути о стенки) своим весом давит на ртуть в чашке, а не на трубку. Как разрешить это противоречие?

Подробнее
Задача по физике – 4958
Был предложен следующий проект «вечного» насоса. На берегу реки ставится железный бак с краном А и трубой В (шлангом), опущенным в реку (рис.). Для того чтобы привести устройство в действие, надо через кран А выкачать из бака воздух и наполнить его водой. Если затем отключить воздушный насос и открыть кран А, то вода (по мнению изобретателя) в силу своей тяжести потечет из крана, а атмосферное давление по трубке В будет поставлять в бак все новые и новые количества воды. В чем ошибка проекта?

Подробнее
Задача по физике – 4959
Сосуд, имеющий форму, изображенную на рисунке, заполнен водой. Радиус отверстия А равен радиусу трубки В. Что произойдет, если вынуть пробку A? Явлениями капиллярности пренебречь.
Решение. Под действием веса жидкость будет вытекать из отверстия А. Одновременно в расширенную часть С будут поступать через трубку В новые количества жидкости.
Опыт опровергает это решение. В чем ошибка рассуждений?

Подробнее
Задача по физике – 4960
Физик древности Герои Александрийский предложил оригинальную конструкцию фонтана (рис.). Вначале сосуд А наполняют водой и некоторое количество воды наливают в сосуд С. Получится ли вечный круговорот воды в системе: сосуд С, трубка 1, сосуд В, трубка 2, сосуд А, трубка 3, струя 4, сосуд С и т. д.?
Так как фонтан является действующей системой (в чем легко убедиться на опыте, соорудив его из консервных банок), то не нарушается ли закон сохранения энергии: вода в струе 4 поднята на более высокий уровень, чем она была в сосуде С?

Подробнее
Задача по физике – 4961
При открытом кране (рис.) через трубку В накачивают резиновый шар С. Он раздувается, и резина растягивается. Закрывают кран и отсоединяют насос. Однако воздух из трубки В не выходит, хотя его и должна выталкивать, сжимаясь, упругая резиновая оболочка шара. Объясните парадокс.

Подробнее
Задача по физике – 4962
В сосуде с водой плавает стакан, в котором находится камень. Как изменится уровень воды в сосуде, если из стакана вынуть камень и опустить его в сосуд?
Решение. При перенесении камня в сосуд общий вес воды, камня и стакана не меняется. Площадь дна сосуда тоже не меняется. Следовательно, давление системы трех тел на дно сосуда не должно измениться. Но давление столба воды на дно сосуда $p = rho gh$, где $rho$ — плотность воды, $g$ — ускорение силы тяжести, $h$ — высота столба. Следовательно, уровень воды в сосуде не должен измениться.
Проделаем соответствующий опыт и убедимся, что уровень воды в сосуде понизится. В чем ошибочность решения?
Подробнее
Задача по физике – 4963
В сосуде со ртутью плавает чугунный брусок. Изменится ли положение центра тяжести бруска по отношению к уровню ртути, если в сосуд налить воды?
Решение. Вода давит на брусок сверху и с боков. Силы давления на брусок с боков уравновешиваются, а сила давления на брусок сверху должна понизить положение центра тяжести бруска по отношению к уровню ртути.
Проделаем соответствующий опыт и обнаружим, что брусок в ртути не опускается, а немного всплывает. В чем ошибочность представленного выше решения?
Подробнее
Задача по физике – 4964
Обычно считают, что сифоном можно переливать жидкость из верхнего сосуда в нижний. Если в большой сосуд с водой поместить два сосуда А и В, причем в первом находится керосин, а во втором – вода (рис.), и соединить их трубкой, то керосин будет переливаться из нижнего сосуда А в верхний сосуд В.
Таким образом, керосин, всплывая, увеличивает свою потенциальную энергию по отношению к Земле. Не противоречит ли этот опыт закону сохранения энергии?

Подробнее
Задача по физике – 4965
Кювета с водой стоит на бруске (рис.). На воде плавает коробочка с гирей. Кювета находится в равновесии.
Если вынуть гирю из коробочки и поставить на дно кюветы под тем местом, где плавала коробочка, то равновесие нарушится (рис.), хотя вес левой части кюветы как будто бы не изменился. Объясните ошибку рассуждений

Подробнее
Задача по физике – 4966
Если в установке, изображенной на рисунке, пережечь нить АВ, то тело Р, имеющее объем 100 $см^{3}$, целиком погружается в воду и остается висеть на нити АСВ. При этом равновесие весов нарушается. На какую чашку весов и какой добавочный груз необходимо положить, чтобы восстановить равновесие?
Решение. В соответствии с законом Архимеда тело Р, погруженное в воду, будет выталкиваться вверх с силой 0,98 н. Поэтому на правую чашку весов будет действовать вес штатива и вес тела Р, уменьшенный на вес вытесненной им воды.
Следовательно, для восстановления равновесия весов необходимо на правую чашку поставить гирю массой 100 г.
Однако опыт показывает, что на правую чашку весов необходимо поставить гирю массой 200 г. В чем ошибка решения?

Подробнее
Задача по физике – 4967
Симметричный относительно вертикальной плоскости ОК сосуд ABCD (рис.) наполнен водой и опирается о ребро неподвижной призмы. В правую часть сосуда опустили кусок алюминия массой 0,5 кг, а в левую — кусок свинца массой 0,4 кг. Какая часть сосуда перетянет?
Решение. Сосуд представляет собой сложный равноплечий рычаг. Так как вес куска алюминия больше, чем свинца, то перетянет правая сторона сосуда, где лежит кусок алюминия.
Опыт, однако, опровергает это заключение. В чем ошибка решения?

Подробнее
Источник
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
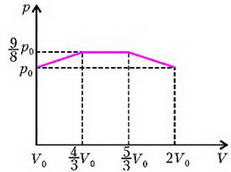
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
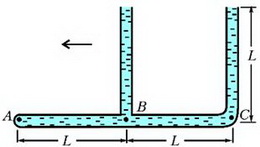
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
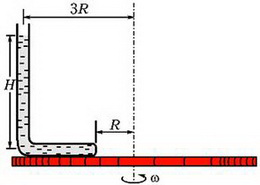
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
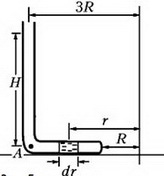
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
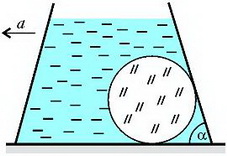
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
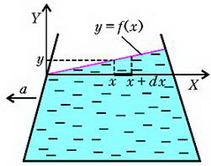
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде —
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
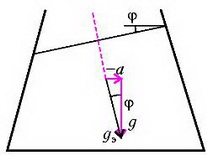
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
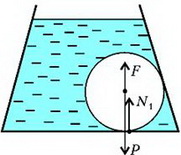
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
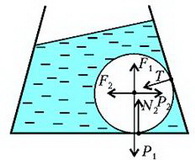
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
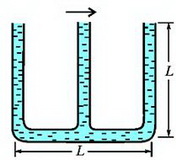
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
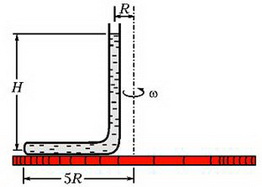
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник
