Из сосуда а в резервуар б

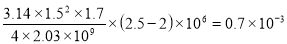
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.

№ 4.

Для испытания на прочность резервуара с водой произведена опресовка под давлением p1. Через сутки давление, вследствие утечки из резервуара, понизилось до p2. Определить величину утечки из резервуара, если модуль упругости воды Е=2.03×109 Па. Резервуар имеет форму цилиндра диаметром d и высотой h.

Дано : p1=2.5 МПа ; p2=2 МПа ; d=1.5 м ; h=1.7 м.

Найти : ΔV

Решение.

Величину утечки определим из формулы коэффициента объёмного сжатия :

βw= (1)

где V – первоначальный объём ; ΔV – изменение объёма при изменении давления на Δp.

В данном случае величина утечки из резервуара равна величине изменения объёма, при изменении давления в резервуаре на Δp. Тогда из (1) находим :

ΔV=-βwVΔp (2)

Здесь Δp=p2-p1 ; βw=1/E (где Е – модуль упругости воды) ; V=. Тогда выражение (2) примет вид :

ΔV= (3)

Вычисления по формуле (3) дают :

ΔV= м3=0.7 л.

Ответ : ΔV=0.7 л.

№ 13.

Цилиндрический сосуд диаметром D и высотой a, заполненный водой, опирается на плунжер диаметром d. Определить показание манометра М и нагрузки на болтовые группы А и B, если масса верхней крышки сосуда m1, цилиндрической части сосуда m2 и нижней крышки сосуда m3.

Дано : D=0.45 м ; a=0.65 м ; d=0.35 м ; m1=350 кг ; m2=200 кг ; m3=170 кг.

Найти : pм ; FA ; FB

Решение.

Из сосуда а в резервуар б

Определим показание манометра :

pм=p0-pатм (1)

где p0 – давление на свободной поверхности жидкости ; pатм – атмосферное давление (pатм=105 Па).

В данном случае p0 равно давлению, производящим верхней крышкой сосуда :

p0= (2)

где G1 – вес верхней крышки сосуда ; S – площадь свободной поверхности жидкости, равный площади крышки диаметра D.

G1=m1g ; S=

С учётом выражений для G1 и S формула (2) примет вид :

p0= (3)

Подставляя (3) в (1), получим :

pм= (4)

Вычисления по формуле (4) дают :

pм= Па=-78.4 кПа.

Т.е. манометр показывает вакуумметрическое давление pм=78.4 кПа.

Определим нагрузку на болтовые соединения группы А. Запишем уравнение равновесия для болтового соединения в проекции на вертикальную ось :

FA=P0-G23 (5)

где P0 – сила давления со стороны жидкости ; G23 – вес цилиндрической и нижней частей сосуда.

P0=p0S ; G23=(m2+m3)g

Тогда выражение (5) примет вид :

FA= (6)

Вычисления по формуле (6) дают :

FA=9.81×(350-200-170)=-196.2 Н

Знак «минус» означает, что нагрузка FA направлена вниз.

Определим нагрузку на болтовые соединения группы B. Составляя уравнение равновесия болтовых соединений на вертикальную ось, получим :

FB=-N-G3 (7)

где G3 – вес нижней крышки сосуда ; N – сила давления жидкости на нижнюю крышку сосуда.

Силу давления на нижнюю крышку сосуда определим по формуле :

N=S1(p0+ρga) (8)

где S1= – площадь нижней крышки сосуда ; ρ=998 кг/м3 – плотность воды при t=20°C (табл. 1. [2]) ; а – глубина погружения нижней крышки 9высота сосуда).

Подставляя (8) в (7) и, учитывая выражения для S1, p0 и G3=m3g, получим :

FB= (9)

Вычисления по формуле (9) дают :

FB= Н

Знак «минус» означает, что нагрузка FB направлена вниз.

Ответ : pм=-78.4 кПа ; FA=-196.2 Н ; FB=-3424 Н.

№ 40.

Жидкость Ж подаётся в открытый верхний бак по вертикальной труде длиной l и диаметром d за счёт давления воздуха в нижнем замкнутом резервуаре.

Определить давление p воздуха, при котором расход будет равен Q. Принять следующие коэффициенты сопротивления : вентиля ξв=8 ; входа в трубу ξвх=0.5 ; выхода в бак ξвых=1. эквивалентная шероховатость стенок трубы kэ=0.2 мм.

Дано : Ж – вода ; Q=10 л/с ; l=10 м ; d=80 мм.

Найти : p

Решение.

Из сосуда а в резервуар б

Составим уравнение Бернулли для двух сечений 0-0 и 1-1 трубопровода :

или

Отсюда находим давление воздуха p :

p= (1)

где p+ρgh и ρgh – давления в соответствующих сечениях ; p – давление воздуха ; ρ=998 кг/м3 – плотность воды при t=20°C (табл. 1 [2]) ; hl – потери напора по длине трубопровода ; hw1, hw2, hw3 – потери напора в местных сопротивлениях вентиля, вход в трубу, выход в бак.

Потери напора по длине трубопровода определим по формуле Вейсбаха-Дарси :

hl= (2)

где λ – коэффициент гидравлического трения ; v – скорость жидкости в трубе (v=4Q/(πd2) ; Q – расход ; l – длина трубопровода ; d – диаметр трубы.

Для нахождения коэффициента гидравлического трения λ, определим число Рейнольдса :

Re= (3)

где ν=0.01×10-4 м2/с – коэффициент кинематической вязкости воды при t=20°C (по табл. 1 [2]).

Вычисления по формуле (3) дают :

Re=

Для чисел Рейнольдса (4000<Re<224000), для определения λ рекомендуется формула Альтшуля :

λ=

или с учётом формулы (3), получим :

λ=

Подставляя выражение для λ в формулу (2), получим :

hl= (4)

Потери напора в местных сопротивлениях находим по формулам :

hw1= (5)

hw2= (6)

hw3= (7)

Подставляя (4), (5), (6) и (7) в формулу (1), получим :

p= (8)

Вычисления по формуле (8) дают :

Па=123 кПа.

Ответ : p=123 кПа

№ 50.

Определить длину трубы l, при которой расход жидкости из бака будет в два раза меньше, чем через отверстие того же диаметра d. Напор над отверстием равен H. Коэффициент гидравлического трения в трубе принять равным λ=0.025.

Дано : H=5 м ; d=50 мм ; Q1=0.5Q2 ; λ=0.025.

Найти : l.

Решение.

Из сосуда а в резервуар б

Составим уравнение Бернулли для двух сечений трубы 0-0 и 1-1 :

H= (1)

где v1 – скорость в сечении 1-1 ; hλ – потери напора по длине тубы.

Потери напора определяются по формуле Вейсбаха-Дарси :

hλ= (2)

где λ – коэффициент гидравлического трения ; Q1 расход в трубе.

Подставляя (2) в (1) и, учитывая что скорость v1 связана с расходом Q1 выражением :

v1=, получим:

Отсюда находим длину трубы :

l= (3)

Расход через отверстие определяется выражением :

Q2= (4)

где μ=0.62 – коэффициент расхода (рекомендации стр. 109 [1]) ; S0 – площадь сечения отверстия (S0=πd2/4) ; H – напор, под которым происходит истечение (глубина погружения отверстия под уровень жидкости в баке).

Учитывая, что по условию Q1=0.5Q2, то подставляя (4) в (3) и, учитывая выражение для S0, получим :

l=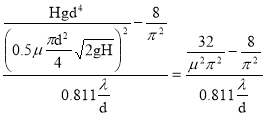 Из сосуда а в резервуар б (5)

Вычисления по формуле (5) дают :

l= м

Ответ : l=18.8 м

№ 58.

Центробежный насос с известной характеристикой откатывает воду из сборного колодца в бассейн с постоянным уровнем H по трубопроводам l1, d1 и l2, d2. При работе насоса с постоянным числом оборотов n=1450 мин-1 определить глубину h, на которой установится уровень воды в колодце, если приток в него Q. При расчётах принять коэффициенты гидравлического трения λ1=0.03 и λ2=0.035 и суммарные коэффициенты местных сопротивлений ζ1=6 и ζ2=10.

Дано : H=14 м ; l1=5 м ; d1=130 мм ; l2=11 м ; d2=80 мм ; Q=7 л/с.

Найти : h

Решение.

Из сосуда а в резервуар б

Напор, развиваемый насосом, расходуется на подъём воды на геометрическую высоту Hг=H+h и преодоление потерь напора во всасывающей и нагнетательной линиях :

Hн=Hг+h1+h2=H+h+h1+h2

Отсюда глубина, на котором установится уровень воды в колодце :

h=Hн-h1-h2 (1)

где Hн – напор, развиваемый насосом при заданном расходе Q (определяется по графику ; при Q=7 л/c, H=22 м) ; h1 и h2 – потери напора во всасывающей и нагнетательной линиях.

Потери напора состоят из потерь напора по длине и в местных сопротивлениях :

h1=hℓ1+hм1 ; h2=hℓ2+hм2

Потери напора по длине определим по формуле Вейсбаха-Дарси :

hℓ1= ; hℓ2=

где λ – гидравлический коэффициент трения.

Скорость движения воды во всасывающей линии :

v1= м/с

Скорость движения жидкости в нагнетающей линии :

v2= м/с.

Потери напора по длине трубопровода для всасывающей линии :

hℓ1= м.

Потери напора по длине трубопровода для нагнетающей линии :

hℓ2= м.

Потери в местных сопротивлениях по формуле Вейсбаха :

для всасывающей линии :

hм1= м ;

для нагнетающей линии :

hм2= м.

Общие потери во всасывающей линии :

h1=0.02+0.09=0.11 м.

Общие потери в нагнетающей линии :

h2=0.47+0.98=1.45 м.

Тогда, искомая глубина, на которой установится уровень воды в колодце :

h=22-0.11-1.45=20.44 м.

Ответ : h=20.44 м.

№ 67.

Вал гидродвигателя Д, рабочий объём которого V0, нагружен крутящим моментом Мк. К двигателю подводится поток рабочей жидкости – масло Ж, температура которого 60°С, с расходом Q. КПД гидродвигателя : объёмный η0=0.96, гидромеханический ηгм.

Определить частоту вращения вала гидродвигателя и показание манометра М, установленного непосредственно перед двигателем, если потери давления в обратном клапане Коб составляют Δpкл=15 кПа. Длина линии равна lc, а диаметр dc. Эквивалентная шероховатость Δэ=0.05 мм.

Дано : Ж – индустриальное 20 ; Q=28 л/мин ; V0=40 см3 ; Mk=25 Н·м ; ηгм=0.9 ; lc=2.8 м ; dc=14 мм.

Найти : n, pм

Решение.

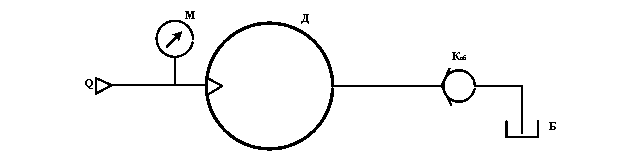
Из сосуда а в резервуар б

Частоту вращения гидродвигателя определим по формуле :

n= (1)

где η0 – объёмный к.п.д. гидродвигателя ; Q – расход рабочей жидкость ; V0 – рабочий объём гидродвигателя.

Вычисления по формуле (1) дают :

n= об/мин.

Определим показание манометра. Давление, создаваемое перед электродвигателем затрачивается на потери давления в гидродвигателе Δp, потери давления в обратном клапане Δpоб, потери давления в сливной линии Δpc :

pм=Δp+Δpоб+Δpc (2)

Потери давления в гидродвигателе определим по формуле :

Δp= (3)

где Мк – крутящий момент на валу двигателя ; ηгм – к.п.д. гидродвигателя.

Вычисления по формуле (3) дают :

Δp= Па=4361.1 кПа.

Потери давления в сливной линии определим по формуле :

Δpc=ρghℓ (4)

где ρ – плотность рабочей жидкости ; hℓ – потери напора в сливной линии.

Определим плотность рабочей жидкости (масло индустриальное 20) при температуре t=60° по формуле :

ρ= (5)

где ρ0=891 кг/м3 (табл. 1 [2]) – плотность рабочей жидкости при t0=50° ; α=0.0007 1/°C (табл. 1 [2]) – температурный коэффициент расширения жидкости ; Δt=t-t0=60-50=10° – изменение температуры.

Тогда вычисления по формуле (5) дают :

ρ= кг/м3

Потери напора в силовой линии по формуле Вейсбаха-Дарси :

hℓ= (6)

С учётом (6) формула (4) примет вид :

Δp= (7)

где λ – коэффициент гидравлического трения.

Коэффициент гидравлического трения λ определим по формуле Альтшуля :

λ= (8)

где Δ – эквивалентная шероховатость ; Re – число Рейнольдса.

Число Рейнольдса определим по формуле :

Re= (9)

где ν=0.14×10-4 м2/с – кинематическая вязкость при t=60° (табл. 1 [2]).

Вычисления по формуле (9) дают :

Re=

Тогда вычисления по формуле (8) дают :

λ=

Вычисления по формуле (7) дают :

Δpc= Па=356 кПа

Окончательно, производя вычисления по формуле (2), найдём показания манометра :

pм=356+15+4361=4732 кПа

Ответ : n=672 об/мин ; pм=4732 кПа.

Источник

Задачи данного раздела рассчитаны на применение уравнения Бернулли для потока реальной жидкости (2.3). Полагая при этом поток турбулентным, коэффициент Кориолиса можно принимать α = 1.

При применении уравнения Бернулли важно правильно выбрать те два сечения, для которых оно записывается.

В качестве сечений рекомендуется брать:

– свободную поверхность жидкости в резервуаре (баке), где скорость потока v = 0;

– выход в атмосферу, где ризб = 0; рабс = ратм;

– сечение, где присоединен тот или иной манометр, пьезометр или вакуумметр;

– неподвижный воздух вдалеке от входа в трубу, в которую происходит всасывание из атмосферы.

Уравнение Бернулли рекомендуется сначала записать в общем виде, а затем переписать с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.

При этом необходимо помнить следующее:

– вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;

– давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);

– суммарная потеря напора Σh всегда пишется в правой части уравнения Бернулли со знаком «+»;

– величина Σh в общем случае складывается из местных потерь, которые можно выражать формулой Вейсбаха (2.4), и потерь на трение по длине, определяемых формулой Дарси (2.6).

Примеры решения задач

Пример 2.1.

Из резервуара А, заполненного водой и находящегося под манометрическим давлением Рм = 0,5 атм, вода подается по стальному трубопроводу длиной l = 10 м и диаметром d = 100 мм в резервуар Б на высоту Н = 2 м. Коэффициент сопротивлений крана ξкр = 9, каждого колена ξкол =0,25; ξвх = 0,5; ξвых = 1. Коэффициент гидравлического трения λ = 0,04. Определить режим течения, расход Q и скорость V воды в трубопроводе.

Решение:

Уравнение Бернулли в общем случае имеет вид:

. (2.9)

Первое сечение (1-1) возьмем на свободной поверхности воды в баке А, второе (2-2) – на свободной поверхности в баке Б. Плоскость сравнения совместим с осью трубопровода в месте соединения его с баком А (см. рисунок).

Давления в первом и втором сечениях возьмем абсолютные. Скоростью изменения уровней воды в баках А и Б можно пренебречь, поэтому в уравнении (2.9) v1 = v2 = 0. Тогда уравнение (2.9) примет вид

Отсюда (учитывая, что Н2 = Н1 + Н) получаем

Режим течения определим по значению числа Рейнольдса:

Т.к. Re > 2300, следовательно, режим турбулентный.

Расход в трубе определится как

Пример 2.2. Определить расход керосина, вытекающего из бака по трубопроводу длиной l = 10 м и диаметром d = 50 мм, если избыточное давление в баке Рм = 16 кПа, высота уровня Н1 = 1 м, высота подъема керосина в открытом пьезометре Н2 = 1,75 м. Труба гидравлически гладкая (шероховатость D = 0). Плотность керосина ρ = 800 кг/м3, кинематическая вязкость n = 0,025 см2/с.

Решение:

Удельный вес керосина γ = ρ · g = 800 · 10 = 8000 Н/м3. Поместим первое и второе поперечные сечения потока, а также плоскость сравнения так, как показано на рисунке. Тогда уравнение Бернулли примет вид:

или

. (2.10)

Воспользоваться уравнением (2.10) мы не можем, т.к. нам неизвестно значение коэффициента гидравлического трения λ. Поэтому дальнейшее решение проводим методом последовательных приближений.

1-е приближение. Задаемся значением λ из диапазона 0,02…0,04.

Пусть λ = 0,02.

Тогда из (2.10) находим скорость:

Далее определяем число Рейнольдса:

Поскольку режим турбулентный, а труба гладкая – коэффициент гидравлического трения λ находим по формуле Блазиуса:

Различие между принятым и получившимся значениями λ составит

Поскольку разница превышает 5%, сделаем второе приближение.

2-е приближение.

Пусть λ = 0,022.

Тогда из (2.10)

Поскольку теперь λ = λ′, приближения заканчиваем.

Расход теперь определится как

Данный метод позволяет с достаточной точностью производить инженерные расчеты.

ЗАДАЧИ К ГЛАВЕ 2

Задача 22. Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н = 2 м и постоянное избыточное давление р2 = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d1 = 75 мм, показывает р1 = 0,25 МПа. Пренебрегая потерями на трение по длине, определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкости к баку, равен d2 = 50 мм; коэффициент сопротивления этой трубы принят равным ζ = 0,5. Плотность жидкости ρ = 800 кг/м3.

Задача 23. Бензин сливается из цистерны по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления ζкр = 3. Определить расход бензина при Н1 = 1,5 м и Н2 = 1,3 м, если в верхней части цистерны имеет место вакуум hвак = 73,5 мм рт. ст. Потерями на трение по длине пренебречь. Плотность бензина ρ = 750 кг/м3.

Задача 24. Вода перетекает из напорного бака А в открытый резервуар Б через вентиль с коэффициентом сопротивления ζв = 3 по трубе. Диаметры: d1 = 40 мм; d2 = 60 мм. Считая режим течения турбулентным и пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты: Н1 = 1 м. Н2 = 2 м; избыточное давление в напорном баке ро = 0,15 МПа.

Задача 25. По длинной трубе диаметром d = 50 мм протекает жидкость (ν = 2 см2/с; ρ = 900 кг/м3). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (Н = 80 см).

У к а з а н и е. Считать, что давление перед отводом расходуется на создание скоростного напора в отводе и подъеме жидкости на высоту h.

Задача 26. Вода течет по трубе диаметром D = 20 мм, имеющей отвод (d = 8 мм). Пренебрегая потерями напора, определить расход жидкости в отводе q, если расход в основной трубе Q = 1,2 л/с; высоты Н = 2 м, h = 0,5 м. Режим течения считать турбулентным.

Задача 27. Масло трансформаторное из большого резервуара, в котором поддерживается постоянный ее уровень, по стальному нержавеющему трубопроводу вытекает в атмосферу. Диаметр трубопровода d = 70 мм, его горизонтальная и наклонная части одинаковой длины l = 3,4 м. Высота уровня жидкости над горизонтальной частью трубопровода равна Н = 6,2 м, конец его наклонной части находится ниже горизонтальной части на величину h = 1,5 м. Плотность масла ρ = 900 кг/м3, кинематическая вязкость ν = 0,2 см2/с. Эквивалентная шероховатость трубопровода Δ = 0,1 мм.

Определить расход Q жидкости и построить пьезометрическую и напорную линии.

Задача 28. Чему должно быть равно манометрическое давление рм на поверхности жидкости в закрытом резервуаре А для того, чтобы обеспечить подачу керосина в количестве Q = 2,5 л/с в открытый резервуар Б? Разность уровней в резервуарах Н = 6,7 м. Чугунный старый трубопровод имеет длину 2l (l = 4,8 м) и диаметр d = 50 мм, эквивалентная шероховатость стенок Δ = 1 мм. Посредине его установлен обратный клапан К, коэффициент местного сопротивления которого ζкл. = 5,5. Построить пьезометрическую и напорную линии. Плотность керосина ρ = 750 кг/м3; кинематическая вязкость ν = 0,02 см2/с

Задача 29. Из бака А жидкость с плотностью ρ = 900 кг/м3 и вязкостью ν = 0,2 см2/с самотеком по алюминиевому трубопроводу длиной l = 72 м попадает в производственный цех. Напор в баке А равен Н = 6 м. Каким должен быть диаметр трубопровода, чтобы обеспечивалась подача жидкости в количестве Q = 2,6 л/с при манометрическом давлении в конце трубопровода не ниже рм = 0,2 МПа? При расчете принять, что местные потери напора составляют 20 % от потерь по длине. Построить пьезометрическую и напорную линии.

Задача 30. Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по чугунному новому трубопроводу, состоящему из двух последовательно соединенных труб, глицерин течет в резервуар Б. Разность уровней жидкости в резервуарах равна Н = 6,8 м. Длина труб l = 6,8 м и l2 = 8,2 м, а их диаметры d = 70 мм и d2 = 50 мм. Плотность глицерина ρ = 1500 кг/м3; вязкость ν = 10 см2/с. Эквивалентная шероховатость труб Δ = 0,6 мм.

Определить расход Q жидкости, протекающей по трубопроводу. В расчетах принять, что местные потери напора составляют 15 % от потерь по длине.

Задача 31. Определить расход воды, протекающей по стальному трубопроводу в пункты 1 и 2, если напор Н в резервуаре постоянный. Длина отдельных частей трубопровода равны l = 13 м, l1 = 13 м, l2 = 10 м, а диаметры d = 40 мм, d1 = 32 мм, d2 = 32 мм. Коэффициент гидравлического трения λ принять равным 0,04. Местные потери напора в расчетах не учитывать.