Из сосуда выливается жидкость

Закон Торричелли

Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
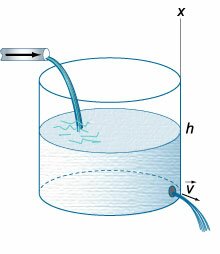
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:

[v = sqrt {2gh} ,]

где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.


Рис.1	Рис.2

Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.

В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)

[v = varphisqrt {2gh} ,]

где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.

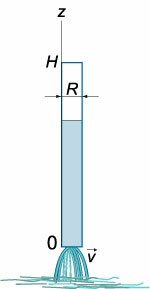
Вытекание жидкости из тонкой трубки

Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.

Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть

[v = kh,]

где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.

Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).

Дифференциальное уравнение вытекания жидкости

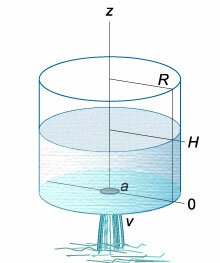
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).


Рис.3	Рис.4

Скорость жидкости описывается формулой Торричелли:

[v = sqrt {2gz} ,]

где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:

[q = – pi {a^2}sqrt {2gz} .]

Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.

Уравнение баланса жидкости в резервуаре описывается следующим образом:

[frac{{dV}}{{dt}} = q.]

Поскольку изменение объема (dV) можно выразить как

[dV = Sleft( z right)dz,]

то мы получаем дифференциальное уравнение

[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]

Подставим функцию (qleft( z right)) в это уравнение:

[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]

Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно

[Sleft( z right) = pi {R^2},]

где (R) − радиус основания цилиндра. Тогда

[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]

В результате получаем уравнение с разделяющимися переменными:

[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]

Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)

[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]

Отсюда следует выражение для полного времени вытекания жидкости (T:)

[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]

Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
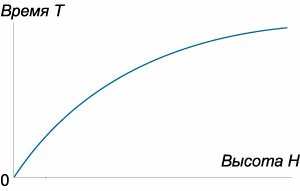
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)

Аналогично можно описать вытекание жидкости и из сосуда другой формы.

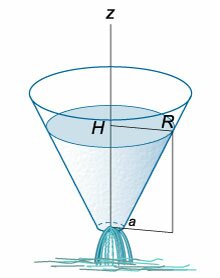
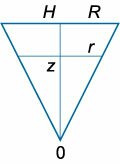
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).


Рис.5	Рис.6

Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением

[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]

где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)

Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:

[qleft( z right) = – pi {a^2}sqrt {2gz} ,]

где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что

[frac{R}{H} = frac{r}{z}.]

Следовательно, площадь поверхности жидкости на высоте (z) будет равна

[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]

Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:

[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]

После простых преобразований получаем следующее дифференциальное уравнение:

[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]

Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)

[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]

Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:

[T = sqrt {frac{{2H}}{g}}. ]

Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?

Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.


Рис.7	Рис.8

Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:

[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]

В данном случае площадь поперечного сечения (Sleft( z right)) является константой:

[Sleft( z right) = S = pi {R^2},]

и поток жидкости, вытекающей из сосуда, определяется формулой:

[qleft( z right) = – kz,]

где (k) зависит от размера отверстия, смачиваемости и других параметров.

В результате получаем простое дифференциальное уравнение:

[pi {R^2}frac{{dz}}{{dt}} = – kz,]

или после разделения переменных:

[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]

Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)

[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]

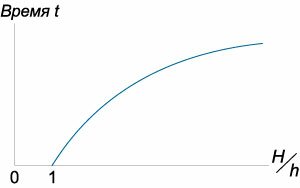
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)

Источник

КАТЕГОРИИ:

Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)

Пользуясь уравнением Бернулли (102.5), легко определить скорость весомой жидкости, вытекающей из сосуда. Пусть жидкость вытекает из сосуда, имеющего сбоку отверстие (рис. 288). Отверстие снабжено специальным «насадком», который направляет струю. При истечении вся жидкость в сосуде придет в движение, и ее можно разбить на трубки тока. Точное разбиение жидкости на трубки тока представляет довольно сложную задачу даже

Рис. 288.

при простой форме сосуда. Но нам нет необходимости знать, как идут трубки тока по всему объему текущей в сосуде жидкости, нам достаточно знать, что все трубки тока начинаются на свободной поверхности жидкости и обязательно проходят через отверстие «насадка».

На свободной поверхности жидкости все трубки тока имеют одинаковую скорость v0,одинаковое давление р0и одинаковую высоту h0, так как поверхность жидкости при истечении опускается вниз, оставаясь горизонтальной, если она значительно выше уровня отверстия. Следовательно, постоянная в уравнении Бернулли (102.5) имеет одинаковую величину для всех трубок тока, равную

(103.1)

Заметим, что так будет всегда, когда течение всех частиц идеальной жидкости начинается из одинакового состояния, и тогда постоянная уравнения Бернулли имеет одинаковое значение не только для данной трубки тока, как мы вывели ранее, а для всего пространства текущей жидкости, занятого частицами, вытекающими при одинаковых условиях. Это еще более упрощает анализ течения.

Так как диаметр отверстия мал по сравнению с высотой жидкости в сосуде, то будем считать давление во всем поперечном сечении струи одинаковым и равным окружающему давлению р0. Также и скорость течения в струе для всех трубок тока можно считать одинаковой и равной v. Следовательно, по уравнению Бернулли (102.5)

(103.2)

или

(103.3)

где h — высота отверстия, a h0 — высота свободной поверхности в сосуде.

Если площадь отверстия составляет ничтожную долю от площади поперечного сечения сосуда, то скорость v0будет ничтожно мала по сравнению со скоростью v и членом с v20 в формуле (103.3) можно пренебречь. Поэтому скорость вытекающей жидкости равна

(103.4)

так как g/r=g — ускорению силы тяжести.

Это так называемая формула Торричелли. Скорость истечения весомой жидкости из отверстия в сосуде равна той скорости, которую получит тело, падая с высоты, равной разности высот отверстия и свободной поверхности h0-h. Отметим, что величина скорости совершенно не зависит от направления к горизонту вытекающей струи. Она будет одинакова, под каким бы углом струя ни вытекала. Поэтому, если направить струю вертикально вверх, то частицы жидкости, как и всякое тело, должны подняться на высоту уровня свободной поверхности жидкости1). Однако из-за трения в жидкости, а главным образом из-за трения о частицы жидкости, падающие вниз, и трения в воздухе струя не достигнет

1) Силы трения (вязкости) при течении воды по резиновой трубке, соединяющей «насадок», из которого вытекает струя, с сосудом, не окажут значительного влияния, если диаметр трубки будет велик по сравнению с диаметром вытекающей струи.

уровня жидкости в сосуде (рис. 289, а). Но если направить струю под небольшим углом к вертикали (рис. 289, б), то она поднимется почти до уровня поверхности жидкости.

Рис. 289.

Справедливость формулы Торричелли можно проверить различными способами. Например, можно наблюдать точку пересечения двух струй, вытекающих в горизонтальном направлении из

Рис. 290.

отверстий, находящихся на разной высоте (рис. 290). Если пренебречь вязкостью, то легко показать расчетом, что струи пересекутся на некоторой горизонтали, лежащей ниже нижнего от-

верстия на некотором расстоянии, равном расстоянию между уровнем жидкости в сосуде и верхним отверстием. Опыт подтверждает это. Особенно наглядны изменения точки пересечения струй при подливании в сосуд значительного количества воды, при котором уровень воды меняется.

Расчет прост. Если скорость вытекающей жидкости определяется по закону Торричелли, то

(смысл обозначений можно видеть на рис. 290). Время падения частицы до точки пересечения в каждой струе определяется по формулам

В точке пересечения струй удаление от сосуда обеих струй одинаково. При падении частиц горизонтальная компонента скорости не меняется, следовательно, v1t1=v2t2;отсюда

или

Дата добавления: 2015-06-28; Просмотров: 3281; Нарушение авторских прав?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Рекомендуемые страницы:

Читайте также:

Источник

Тема. Решение задач по теме “Гидростатика и гидродинамика”.

Цели:

– рассмотреть основные приемы решения расчетных задач на тему “Гидростатика и гидродинамика”.

Ход занятия

В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач.

Прежде чем приступить к выполнению задания, следует повторить основные законы гидромеханики.

Основной закон гидростатики – закон Паскаля, согласно которому в состоянии равновесия давление жидкости в данной точке не зависит от ориентации площадки, на которую она действует.

Поскольку в школьном курсе рассматривается стационарное течение несжимаемой жидкости, то будет справедливо уравнение неразрывности струи.

Для идеальной жидкости выполняется уравнение Бернулли. Покажите, что уравнение Бернулли является следствием закона сохранения энергии.

Качественные задачи

К концам равноплечного рычага подвесили две одинаковые гири. Что произойдет, если одну гирю поместить в воду, а другую в керосин?
Ответ: равновесие нарушится.
Почему, если близко стоишь около быстро идущего поезда, возникает эффект “притягивания” к колесам?
Ответ: проходящий поезд увлекает за собой примыкающие к нему слои воздуха. Воздух, движущийся между человеком и поездом, оказывает на него меньшее давление, чем неподвижный. Эта разность давлений и обусловливает силу, увлекающую человека к поезду.
При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял свой самолет. Как можно объяснить это явление?
Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Ответ: чем сильнее вы вдуваете воздух, тем плотнее фильтр входит в воронку. Объясняется это с помощью закона Бернулли, согласно которому давление понижается в местах сужения. В узком просвете между воронкой и бумажным фильтром давление понижается, и внешнее атмосферное давление удерживает фильтр в воронке.

Примеры решения расчетных задач

Задача 1. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S1, сечение струи S2 (рис. 2). Найдите ускорение, с которым перемещается уровень воды в сосуде.

Решение:

Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать

S1v1 = S2v2, (1)
где v1 – скорость воды в сосуде, v2 – скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1)

,
где – ускорение воды в сосуде, – ускорение свободного падения, так на выходе из сосуда вода начинает свободно падать. Таким образом,

Ответ: .

Задача 2. В сосуде с жидкостью сделано отверстие площадью S. Размеры отверстия малы по сравнению с высотой столба жидкости. В одном случае отверстие закрыто пластинкой и измеряется сила давления жидкости на пластинку F1 при высоте столба жидкости h (рис. 3). В другом случае тот же сосуд стоит на тележке, отверстие открыто, и измеряется сила отдачи F2 при установившемся токе жидкости в момент, когда высота столба жидкости будет та же, что и в первом случае. Будут ли силы F1 и F2 равны?

Решение:

Согласно закону Паскаля давление на жидкость передается во всех направлениях одинаково, поэтому в первом случае давление, производимое на пластинку жидкостью, равно гидростатическому давлению столба жидкости высотой h, а значит, F1 = ρghS , где ρ – плотность жидкости.

Во втором случае сила F2 согласно второму закону Ньютона равна изменению импульса жидкости в единицу времени

Читайте также: Чай при болезни сосудов

.
Изменение импульса Δp = Δmv , где Δm – масса жидкости, вытекающей в единицу времени, v – скорость истечения жидкости из отверстия.

Масса вытекающей жидкости Δm = ρgS, скорость истечения согласно формуле Торричелли . Следовательно,

F2 = ρv2S = 2ρghS.

Таким образом, F2 = 2F1 . Объяснить это можно так. Когда жидкость вытекает из малого отверстия, линии тока вблизи него сгущаются, а значит, как следует из уравнения Бернулли, давление на стенку вблизи отверстия уменьшается. Поэтому сила реакции вытекающей струи оказывается больше силы статического давления на площадь отверстия.

Ответ: силы F1 и F2 не равны.

Задача 3. Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b (рис. 3). Сколько воды вытечет из крана за время t?

Решение:
Воспользуемся условием стационарности течения несжимаемой жидкости

. (1)
Для идеальной жидкости справедливо уравнение Бернулли:

.
Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:

. (2)
За время t через любое сечение протекает один и тот же объем воды, поэтому можно записать

. (3)
Выразим скорость v1 из (1) и (2):

.
Подставим полученное значение v1 в (3) и получим окончательный ответ:

Ответ: .

Задача 4. Площадь поршня в шприце S1 = 2 см2, а площадь отверстия S2 = 1 мм2 (рис. 4). Сколько времени будет вытекать вода из шприца, если действовать на поршень с силой F = 5 H и если ход поршня l = 5 см?

Решение:

Так как из шприца вытечет вся находившаяся в нем жидкость, то

S1l = S2v2t, (5)
где v2 – скорость истечения струи. Будем считать жидкость идеальной, тогда можно использовать уравнение Бернулли:

.
Шприц расположен горизонтально, следовательно, h = const. Уравнение Бернулли тогда запишется следующим образом:

, (6)
где Ра – атмосферное давление, а v1 – скорость движения поршня. Из уравнения неразрывности следует

S1v1 = S2v2. (7)
Решая совместно уравнения (6) и (7), получим

,
отсюда

.
Подставляя найденное значение v2 в (5), получим

.
Так как S2S1 , то можно записать

Ответ:

Задачи для самостоятельной работы

“Вечерело. Уставший за нелегкий трудовой день Абдулла Ибн Сауд присел на берегу реки и стал обдумывать свой социальный статус. В колхоз не берут, кооперативы эмир разогнал, к нему самому на службу устраиваться – так стражники без золотых во дворец не пускают. Эх, жизнь… Но тут взгляд Абдуллы остановился: по реке плыл какой-то предмет, и лишь маленький кусочек сургуча был виден над водой. Абдулла бросился в воду и вытащил оттуда старинный глиняный кувшин, герметично закупоренный сургучом. Распечатав кувшин и перевернув его, Абдулла обомлел: сверкнуло золото. Из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а сосуд запечатал и бросил обратно в воду. Поплыл сосуд дальше, примерно треть его объема торчало над водой”.
Так говорится в одной из восточных сказок. Предполагая, что кувшин был двухлитровый, оцените массу одной золотой монеты.
Ответ: m = 4,45 г.
На некоторых железных дорогах пополнение паровозного котла водой производится без остановки паровоза. Для этой цели применяется изогнутая под прямым углом труба, которая опускается на ходу паровоза в канаву с водой, проложенную вдоль рельсов. При какой скорости паровоза вода может подняться на высоту 3 м?
Ответ: v = 28 км/ч.
Из поднятого на высоту h резервуара выходит труба постоянного сечения S, переходящая в короткую трубу сечением S1, перекрытую краном. Найдите давление в магистральной трубе при открытом кране.
Ответ: Р = Ратм + ρgh.
Определите расход воды Q, протекающей через слив плотины, имеющей ширину l, глубину потока d и понижение уровня потока по сравнению с уровнем воды в водохранилище, равное h.
Ответ: Q = ρdl·√(2gh).
Какова примерно скорость катера, если при его движении вода поднимается вдоль его носовой части
на высоту h = 1 м?
Ответ: v ≈ √(2gh) ≈ 4,4 м/с.
На гладкой горизонтальной поверхности стоит цилиндрический сосуд с водой. В боковой стене сосуда у дна имеется отверстие площадью S0. Какую силу нужно приложить к сосуду в горизонтальном направлении, чтобы удержать его в равновесии? Площадь поперечного сечения сосуда равна S, высота столба жидкости h.
Ответ: .
На поршень шприца площади S действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади s? Плотность жидкости ρ. Трением пренебречь.
Ответ: . Если s S, то .

Рекомендуемая литература

Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 332-352.
Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 420-436.
Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 63-67.
Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр “Март”, 2004. – С. 184-212.

Источник