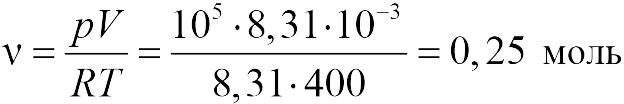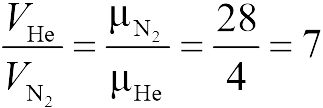Изменение объема газов в сосудах

Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
| (13.1) |
где ![]() — давление газа,
— давление газа, ![]() — концентрация молекул газа (число молекул в единице объема),
— концентрация молекул газа (число молекул в единице объема), ![]() — постоянная Больцмана,
— постоянная Больцмана, ![]() — абсолютная (в шкале Кельвина) температура. Учитывая, что
— абсолютная (в шкале Кельвина) температура. Учитывая, что ![]() , где
, где ![]() — число молекул газа,
— число молекул газа, ![]() — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
— объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
| (13.2) |
Число молекул ![]() можно связать с количеством вещества газа
можно связать с количеством вещества газа ![]() :
: ![]() , где
, где ![]() — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
— число Авогадро. Поэтому формулу (13.2) можно переписать в виде
| (13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как ![]() . Постоянная
. Постоянная ![]() = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу
= 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу ![]() и молярную массу этого газа
и молярную массу этого газа ![]()
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где ![]() — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
— постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где ![]() — постоянная при постоянном объеме.
— постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где ![]() — постоянная. Отсюда следует, что графиком зависимости
— постоянная. Отсюда следует, что графиком зависимости ![]() от
от ![]() в изотермическом процессе является гипербола.
в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов ![]() определяется суммарным числом молекул всех компонент смеси:
определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где ![]() — число молекул первой, второй, третьей и т.д. компонент смеси,
— число молекул первой, второй, третьей и т.д. компонент смеси, ![]() — постоянная Больцмана,
— постоянная Больцмана, ![]() — абсолютная температура смеси,
— абсолютная температура смеси, ![]() — объем сосуда. Величины
— объем сосуда. Величины ![]() , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
, имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса ![]() :
:
|
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
|
где ![]() — искомый объем. Сравнивая первую и вторую формулы, заключаем, что
— искомый объем. Сравнивая первую и вторую формулы, заключаем, что ![]() (ответ 1).
(ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
|
где ![]() — неизвестная температура. Из сравнения этих формул получаем
— неизвестная температура. Из сравнения этих формул получаем ![]() , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
, т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
|
Отсюда ![]() , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
, т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. 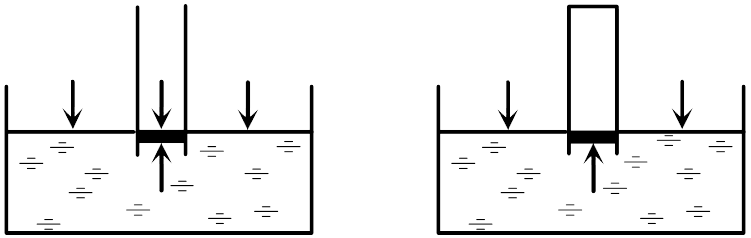 Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
 Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
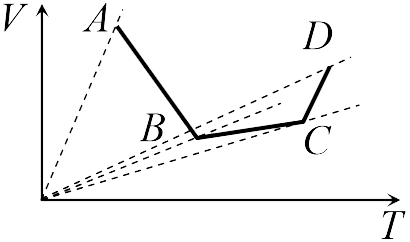
 Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме ![]() (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода
(13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода ![]() и гелия
и гелия ![]() в задаче 13.2.1 равно 2 (ответ 2).
в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры ![]() и массы газов
и массы газов ![]() по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
Если бы точки, отвечающие состояниям 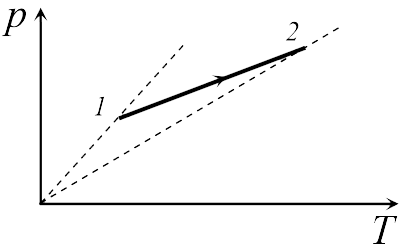 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед ![]() в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается
в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается ![]() (ответ 2).
(ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку ![]() (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
(поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном ![]() и начальном
и начальном ![]() состояниях получаем
состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа ![]() и гелия
и гелия ![]() в сосуде в задаче 13.2.7 имеем
в сосуде в задаче 13.2.7 имеем ![]() (ответ 2).
(ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
|
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода ![]() (т.е. половина моля) и 3 • 1023 молекул гелия
(т.е. половина моля) и 3 • 1023 молекул гелия ![]() (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
(тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь ![]() — масса газа,
— масса газа, ![]() — масса одной молекулы газа.
— масса одной молекулы газа.
Источник
Вот и подходит к концу изучение газов. Кто-то скажет: “Слава Богу!”, а мне жаль. Согласна, задачи на газы – одни из самых сложных. Логически сложных. Они заставляют наш мозг смотреть на химию совсем другими глазами – системно, учат абстрагироваться. Если вы серьезно пройдете через “газовую атаку”, вы станете другим. Это сложно, психологически больно (многие ученики, реально, плачут), но это очень эффективно! Сегодня мои ребята – совсем другие. Это уже не те желторотики, которые пришли ко мне два месяца назад. И хотя до Ломоносова им еще далеко, но, благодаря газам, они уже мыслят и рассуждают по-взрослому.
Такие серьезные изменения в понимании химии, анализе заданий, решении задач, не могут остаться незамеченными. Первыми их начинают чувствовать школьные учителя химии. И что? В лучшем случае они стараются ничего не замечать, в худшем – ревностное отношение к ребенку и гнобление по поводу и без повода. И пошел-поехал цирк с конями. “Репетитор – аферист, он только деньги берет и ничему не учит! Приходите ко мне – я вас научу всему и даже больше! Не хотите? Скоро контрольная – он (она) не напишет! Я трупом лягу, но до ЕГЭ его (ее) не допущу! Позор на мою голову и на всю школу!”
Ровно десять лет назад привели ко мне десятиклассницу Настю Х. Мы учили газы и решали задачи на изменение объема. Мама Насти рассказала о том, что ее дочь весь 9-й класс работала с репетитором, роль которого исполняла школьная учительница. Занимались два раза в неделю по 2 часа. Я ожидала увидеть вполне подготовленное дитя (год с хорошим репетитором – это очень круто!). Объясняю решение задачи. Настя пыхтит-пыхтит, потом не выдержала. “Это – что?! Химия?!” – робко спросила она. “Конечно, химия! – сказала я и задала вполне естественный вопрос: “А что ты делала с репетитором целый год?!” “Химию учила”. “Какую химию? Что учила?” Прежде, чем продолжить, сядьте, чтобы не упасть, и держитесь за ручки кресла. “Мы с учителем лепили модели молекул из пластилина”. Еще раз, для тех, кто не понял.
ЛЕПИЛИ!
МОДЕЛИ МОЛЕКУЛ!
ИЗ ПЛАСТИЛИНА!
ДВА ЧАСА!
ДВА РАЗА В НЕДЕЛЮ!
ГОД!
ЗА ДЕНЬГИ!!!
500 РУБЛЕЙ ЧАС!!!
Конечно, это, скорее, исключение, чем норма (я надеюсь), но перлы о школьных учителях я слышу каждый год из уст моих учеников. О тех учителях, кому вы доверили своих детей, и от которых уйти невозможно. Как быть? Мой добрый совет – не рассказывайте школьным преподавателям о том, что вы работаете с репетитором. На вопрос: “Откуда ты это знаешь?”, отвечайте: “Это вы меня научили!” И химичкам хорошо, и вы не попадете под горячую руку амбициозного “педагога”. Я не учу обманывать – это маленькая хитрость. С волками жить – по волчьи выть. Либо по волчьи выть, либо съедену быть. Поэтому, никогда не делитесь с химичками авторскими алгоритмами, а занятия с репетитором пусть будут вашим маленьким секретом.
Кстати, кем стала девочка Настя, вы узнаете в конце статьи, когда решите все задачи и разберетесь с особенностями авторской фишки.
Однако, вернемся к основной теме. В статье “Секретная шпаргалка по химии. 4.3. Горение смеси газов” я рассказала о гипотетических (предполагаемых) алгоритмических приемах для 28 задания ЕГЭ и подробно описала первую фишку:
1) Расчеты по уравнениям реакции горения смеси газов, состав которой нужно определить предварительно
2) Определение объемного состав смеси по участникам процесса горения (задачи на систему уравнений с двумя неизвестными)
3) Определение состава смеси газообразных продуктов, если в условии избыток-недостаток, степень превращения или выход реакции
4) Задачи на изменение объема газовой смеси в процессе реакции
В статье “Секретная шпаргалка по химии. 4.4. Смеси газов и уравнения с двумя неизвестными” я рассказала о второй предполагаемой фишке “Определение объемного состав смеси по участникам процесса горения (задачи на систему уравнений с двумя неизвестными)”.
В статье “Секретная шпаргалка по химии. 4.5. Избыток-недостаток, степень превращения, выход реакции в смеси газов” я рассказала о третьей предполагаемой фишке: “Определение состава смеси газообразных продуктов, если в условии избыток-недостаток, степень превращения или выход реакции”.
Сегодня мы поговорим о последней, четвертой, фишке “Задачи на изменение объема газовой смеси в процессе реакции”. Это очень интересные задачи! Я их обожаю, поскольку считаю своими “крестными”. Стандартный алгоритм решения такого типа задач – очень громоздкий, тяжелый и сложный. Лет двадцать назад я разработала авторский алгоритм, простой и понятный. Его рабочее название – “Задачи на изменение объема”. Алгоритм решения строится по схеме ΔV (по условию) = ΔV (по уравнению). В результате, решение задач упростилось на порядок. Настоятельно советую разобрать эти задачи, элементы которых уже встречались в 34-х и 35-х заданиях ЕГЭ и могут встретиться в усложненных вариантах 28-го задания. Итак, поехали!
Решим задачи на изменение объема газовой смеси в процессе реакции, используя Четыре Заповеди. Каждое действие обводится зеленым овалом. Читайте внимательно и обязательно записывайте решение каждого задания. После проработки статьи попробуйте самостоятельно решить все разобранные задачи.
Задание 28*(1)
В закрытом сосуде взорвали 60 мл смеси О2 и Н2. Объем паро-газовой смеси, в котором вспыхивает тлеющая лучина, составил 48 мл. Определить состав исходной газовой смеси.
1. Первая Заповедь. Выписать данные задачи в разделе “Дано”.
2. Вторая заповедь. Написать уравнение реакции.
3. Третья заповедь. Сделать предварительные расчеты
Это очень важная часть, поэтому разберем ее подробно. Именно здесь спрятан авторский алгоритм решения (авторская фишка). Пойдем по-порядку. Первое, что необходимо сделать – провести анализ газов-реагентов для определения избытка-недостатка. Обратимся к условию. “Объем паро-газовой смеси, в котором вспыхивает тлеющая лучина…” – дает нам информацию: во-первых, вода после реакции находилась в парообразном состоянии и занимала определенную часть объема продуктов, во-вторых, кислород был в избытке (лучина вспыхивает только при наличии кислорода), в-третьих, водород был в недостатке и сгорел полностью (столько, сколько его было в исходной смеси)
Далее строим алгоритм расчетов по схеме ΔV (по условию) = ΔV (по уравнению). ΔV (по условию) определяем по разнице объемов реагентов и продуктов. ΔV (по уравнению) рассчитываем по уравнению реакции, принимая за неизвестное Х объем газа, который в недостатке. Затем приравниваем ΔV (по условию) = ΔV (по уравнению) и находим Х. Таким образом, авторский алгоритм помог сделать легкие предварительные расчеты по определению объемов каждого газа в исходной смеси.
4. Четвертая заповедь. Составить алгоритм решения задачи.
Вопрос задачи “Определить состав исходной газовой смеси” подразумевает, что требуется рассчитать объемные доли по стандартной формуле. Это удобно сделать в таблице
Задание 28*(2)
К 20 мл смеси ацетилена и азота прибавили 60 мл кислорода. После реакции объем смеси стал равен 56 мл. Определить состав исходной смеси и ее плотность по воздуху.
Задание 28*(3)
14 л смеси бутана с избытком кислорода (н.у.) подожгли. После приведения к н.у. объем газовой смеси стал 8,75 л. Определите объемный состав конечной газовой смеси.
Можете попробовать самостоятельно решить одну из самых несложных задач И.Ю. Белавина. Если вы хорошо разобрались с авторским алгоритмом, у вас все получится.
И.Ю. Белавин, 2005, задача 215
“К 100 мл смеси метана, метиламина и азота добавили 250 мл кислорода и полученную смесь газов взорвали. После охлаждения и конденсации воды объем смеси составил 240 мл, а после пропускания ее через избыток раствора гидроксида натрия он уменьшился до 180 мл. Определите объемный состав исходной газовой смеси. (Ответ: V(СН4) = 20 мл, V(СН3NН2) = 40 мл и V(N2) = 40 мл)”
Задачи решили? Понравилось работать с авторским алгоритмом? Выполняю обещание. Знакомьтесь! Умница и красавица Анастасия Храмченкова! Занималась со мной два года – 10-й и 11-й классы. В 2009 г. поступила в Первый МГМУ им. И.М. Сеченова, сдав блестяще и ЕГЭ, и ДВИ. В 2015 г. закончила обучение с красным дипломом! В настоящее время – клинический ординатор в Медицинском Центре Москвы.
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии https://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Звоните мне +7(903) 186-74-55. Приходите ко мне на курс, на Мастер-классы “Решение задач по химии” – и вы сдадите ЕГЭ с высочайшими баллами, и станете студентом престижного ВУЗа!
PS! Если вы не можете со мной связаться из-за большого количества звонков от моих читателей, пишите мне в личку ВКонтакте, или на Facebook. Я обязательно отвечу вам.
Репетитор по химии и биологии кбн В.Богунова
Источник