Изучение относительного покоя жидкости во вращающемся сосуде
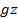
Рассмотрим случай, когда на жидкость, помимо объемных сил тяжести, действует еще другая система объемных сил, например, система центробежных сил инерции.
Возьмем круглоцилиндрический сосуд, наполненный жидкостью, причем будем считать, что этот сосуд вращается вокруг своей вертикальной оси равномерно, т. е. с постоянной угловой скоростью (рис. 2-14). Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Силы трения при этом внутри жидкости, а также между жидкостью, стенками сосуда и его дном, будут отсутствовать.
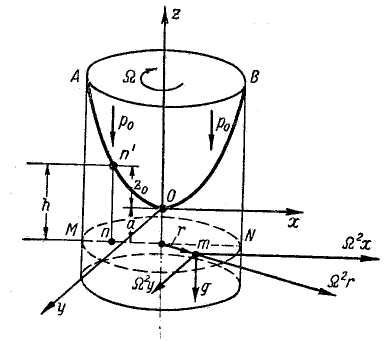
Рис. 2-14. Цилиндрический сосуд, вращающийся относительно вертикальной оси Oz
АОВ — свободная поверхность жидкости
Если оси координат, расположенные, как показано на чертеже, будем считать скрепленными с вращающимся сосудом, то по отношению к таким вращающимся осям координат жидкость также будет находиться в покое. Поэтому для исследования вращающейся жидкости при указанных подвижных осях координат могут быть применены известные уравнения Эйлера (2-14).
В эти уравнения входит объемная сила , действующая на единицу массы жидкости. В данном случае сила будет слагаться из двух сил: силы тяжести и центробежной силы.
С тем чтобы найти проекцию центробежной силы на оси координат, наметим внутри жидкости точку т и выделим у нее элементарную массу жидкости δM. Масса δM будет вращаться вокруг оси сосуда, двигаясь по окружности, имеющей радиус r и лежащей в плоскости, нормальной к оси сосуда. Центробежная сила, действующая на данную массу, будет
I’= , (2-62)
где υ – скорость движения массы δM по окружности радиуса r.
Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной в точке т,
I = = Ω2r. (2-63)
Эта сила, так же как и сила I’, направлена по радиусу от оси сосуда наружу. Проекции силы I (отнесенной к единице м- ассы) на оси координат
Ix = Ω2rcos(r,x) = Ω2x
Iy = Ω2rcos(r,y) = Ω2y
Iz = 0 (2-64)
Проекции объемной силы тяжести, отнесенной к единице массы, выражаются зависимостью (2-28). Складывая объемные силы тяжести и объемные центробежные силы, отнесенные к единице массы, получаем
= 0 +Ω2x = Ω2x;
= 0 + Ω2y = Ω2y;
= – (2-65)
Подставляя (2-65) в (2-17), найдем
dpA = ρ(Ω2xdx + Ω2ydy – , (2-66)
что после интегрирования дает
dpA = ρ( + – ) + C = (x2 + y2) – ρ C. (2-67)
Постоянную интегрирования С устанавливаем, написав (2-67) применительно к точке, находящейся в начале координат, для которой x = y = z =0; p = p0. Как видно,
C = p0 (2-68)
причем (2-67) перепишется в виде:
pA = p0 + (x2 +y2) – γz (2-69)
Это последнее уравнение и выражает закон распределения давления в рассматриваемой жидкости. Пользуясь таким уравнением, можно найти поверхности равного давления.
Действительно, уравнение поверхности, во всех точках которой давление pA = pi= const, запишется в виде
(x2 +y2) – γz = pi – p0. (2-70)
Уравнение (2-70) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью).
Свободная поверхность жидкости, характеризуемая постоянным давлением pi = p0, представляет собой также параболоид вращения; уравнение ее будет:
(x2 +y2) – γz = 0. (2-71)
Если учесть, что x2 + y2 = r2, то, решив (2-71) относительно z, получим следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:
z0 = r2 (2-72)
где z0- ордината кривой АОВ.
Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину a, можно найти, пользуясь (2-69):
pA = p0 + (x2 +y2) +γa = p0 + ρ r2+ γa = p0 + γ( r2+ a). (2-73)
Учитывая (2-72), получаем
pA = p0 + γ(a + z0) = p0 + γh (2-74)
где h = a +z0 показано на рис. 2-14.
Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью того же вида, что и для случая тяжелой покоящейся жидкости [см. (2-39)]; под величиной h здесь надо понимать только заглубление рассматриваемой точки под криволинейной свободной поверхностью.
Источник
Страницы работы
Содержание работы
Министерство
образования Российской Федерации
ГОУВПО
“Комсомольский-на-Амуре государственный
технический университет”
Кафедра “Кораблестроение”
ИЗУЧЕНИЕ
ОТНОСИТЕЛЬНОГО ПОКОЯ ЖИДКОСТИ ВО ВРАЩАЮЩЕМСЯ СОСУДЕ
Методические указания к
лабораторной работе по курсам
“Гидравлика, гидромашины
и гидропривод”,
“Прикладная механика
жидкости и газов”,
“Гидравлика и
гидромашины”,
“Гидрогазодинамика”
Комсомольск-на-Амуре 2003
УДК 621.225
Изучение относительного покоя жидкости во вращающемся сосуде / Сост.
А.В.Космынин, И.В.Каменских – Комсомольск-на-Амуре:
«Комсомольский-на-Амуре гос. тех. ун-т», 2003. – 6 с.
Представлены основные выражения для расчета
параметров формы свободной поверхности жидкости во вращающемся сосуде. Описаны
лабораторная установка и методика обработки данных.
Методические указания рекомендуются для студентов
специальностей 330100, 230300, 552600, 140200, 120300, 120500, 120100, 290500,
170500, 551800, 130100.
Печатается по постановлению
редакционно-издательского совета ГОУВПО «Комсомольский-на-Амуре государственный
технический университет».
Согласовано с отделом стандартизации и метрологии.
Рецензент В.С. Виноградов
Цель работы: построить линию
свободной поверхности в координатах x–z, сравнить линию построенную на
основании опыта, с полученной аналитическим путем.
1 ОБЩИЕ ПОЛОЖЕНИЯ
Вертикальный цилиндрический
сосуд (см. рисунок 1), наполненный капельной жидкостью, вращается вокруг своей
вертикальной оси с постоянной угловой скоростью w. Заключенная в нем жидкость, вследствие ее
вязкости увлекаемая сосудом, вращается вместе с ним с той же угловой скоростью
и, следовательно, находится в покое относительно сосуда. Требуется построить
свободную поверхность жидкости во вращающемся сосуде, пользуясь теоретическими
и опытными данными, и сравнить полученные результаты.
Для определения аналитическим
способом формы свободной поверхности жидкости во вращающемся сосуде
воспользуемся дифференциальным уравнением поверхностей равного давления,
справедливым в случае покоя жидкости (абсолютного или относительного) и
имеющим вид
,
(1)
где X, Y, Z– проекции на соответствующие
оси координат объемных сил, действующих на жидкость и отнесенных к единице
массы ее; dx, dy, dz– произвольные приращения координат.
В рассматриваемом нами случае относительного покоя
жидкости на нее действуют объемные силы:
1. Сила тяжести, направленная
вертикально вниз: величина ее в любой точке равна массе жидкости m сосредоточенной в этой точке,
умноженной на ускорение силы тяжести g.
2. Центробежная сипа инерции,
направленная по радиусу цилиндра от оси вращения; величина ее в некоторой
точке, находящейся на расстоянии r от этой оси, для массы жидкости m, сосредоточенной в данной
точке, равна .
Взяв начало координат в точке О
пересечения свободной поверхности с осью вращения сосуда и направив оси
координат, как показано на рисунке 1, получим следующие значения.
;
;
.
Подставляя эти значения X, Y, Zв уравнение (1), получим
.
Интегрируя это уравнение имеем:
,
откуда
.
(2)
В рассматриваемом случае относительного покоя
капельной жидкости полученное уравнение (2) является уравнением поверхностей
равного давления, образующих семейство параболоидов вращения вокруг оси.
Постоянную интегрирования для
свободной поверхности жидкости, также являющейся поверхностью равного давления,
определим из того условия, что для нее при x=y=0 и z=0.
Тогда получим, что С=0.
Подставляя это значение С в уравнение (2) и имея в виду,
что , получим в выбранной системе
координат следующее уравнение свободной поверхности жидкости во вращающемся
сосуде:
.
(3)
Пользуясь этим уравнением при
заданной угловой скорости вращения сосуда (n – частота вращения вала, мин-1), легко построить свободную
поверхность жидкости в нем.
Определение формы свободной поверхности жидкости во
вращающемся сосуде производится с помощью специального прибора (см. рисунок 1).
2 ВЫПОЛНЕНИЕ ОПЫТА
Для проведения опыта по
определению формы свободной поверхности жидкости во вращающемся сосуде сначала
определяют величину угловой скорости его вращения и после того, как установится
покой жидкости относительно сосуда, с помощью мерной иглы измеряют расстояние
по вертикали от планки Г до свободной поверхности жидкости
в различных точках, находящихся в момент измерения в плоскости диаметрального
сечения сосуда, параллельной планке Г. Измерив такие расстояния при разных значениях радиуса r, определяемого по делениям
планки Г, по точкам строят искомую
свободную поверхность жидкости во вращающемся сосуде и сравнивают ее со
свободной поверхностью, найденной на основании теоретических вычислений по
уравнению (3), при тех же, что и в опытах, значениях w и r.
| ||
Это дает возможность выяснить, в
какой мере результаты теоретических вычислений подтверждаются опытами.
Все результаты опытных
наблюдений, измерений и необходимых
вычислений сводятся в таблицу 1.
Таблица 1 – Результаты
n/n | Отчет по мерной | z, см | Погрешность | |
Опытные значения | Теоретические | |||
Поданным
таблицы необходимо построить две свободные поверхности жидкости во вращающемся
сосуде; одна – соответствующая теоретическим вычислениям, а другая – опытным
данным.
3 ТРЕБОВАНИЯ К ОТЧЕТУ
Отчет по работе должен
содержать:
· схему установки и ее краткое
описание;
· основные теоретические
положения;
· таблицу опытных данных;
· графическое изображение линии
свободной поверхности, полученной на основании опыта и аналитическим путем;
· краткие выводы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.
Башта Т.М. и
др., Гидравлика, гидравлические машины и гидравлические приводы, 1982. – 423 с.
2.
Задачник по
машиностроительной гидравлике /Под ред. И.И. Куколевского и Л.Г. Подвидза. –
М.: Машиностроение, 1981. – 464 с.
Похожие материалы
- Сифонный трубопровод: Методические указания к лабораторной работе
- Напорное неустановившееся движение жидкости. Гидравлический удар
- Экспериментальная проверка основного закона гидростатики: Методические указания к лабораторной работе
Информация о работе
Тип:
Методические указания и пособия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Источник
Цель работы
Исследование зависимости формы свободной поверхности жидкости от угловой скорости вращения цилиндрического сосуда относительно его вертикальной оси симметрии.
При выполнении работы необходимо:
- • экспериментально определить z0 on и горизонтальные координаты точек кривой свободной поверхности жидкости, вращающейся вместе с сосудом с угловой скоростью
- • теоретически определить z0Teop при значении взятом из опытов;
- • сопоставить опытные и теоретические значения величин z0;
- • сопоставить глубину параболоида вращения при двух различных угловых скоростях со
- • построить теоретические и опытные кривые свободной поверхности равномерно вращающейся жидкости при двух различных угловых скоростях со
- • определить частоту вращения сосуда со по известным из опыта координатам свободной поверхности z0on.
Описание опытной установки
Исследования проводятся на установке ГД-2, позволяющей экспериментально определить форму свободной поверхности жидкости во вращающемся сосуде (рис. 4.3). Установка состоит из корпуса (1), цилиндрического сосуда (2) радиусом г = 0,08 м, заполненного на 0,6 своей высоты маслом и приводимого во вращение через червячный редуктор электродвигателем, измерительной иглы (3), рукояти (4), шкал (5) и (6), размещенных на направляющей (7) рукояти (8), панели (9) с расположенными на ней тумблером и лампочкой (11), индикатора (12) для регистрации частоты вращения сосуда с жидкостью, регулятора частоты вращения (13).
Методика и порядок проведения испытаний
Поворотом тумблера (10) (рис. 4.3), расположенного на панели (9), включается электродвигатель и приводится во вращение сосуд (2) с жидкостью.
Вращением регулятора (13) устанавливается заданная частота вращения сосуда, величину установленной частоты вращения определяют по стрелочному счетчику оборотов (12).
Через 2-3 мин, т.е. после того как жидкость в сосуде придет в состояние относительного покоя (по отношению к стенкам вращающего сосуда), начинают производить измерения координат свободной поверхности жидкости. Для этого вращением рукояти (4) мерную иглу (3) устанавливают так, чтобы ось иглы совпадала с осью сосуда (отметка “0” на горизонтальной шкале). Затем вращением рукояти (3) измерительную иглу опускают до соприкосновения её острия со свободной поверхностью жидкости и производят отсчет по нониусу иглы. После этого иглу поднимают вверх и перемещают в горизонтальном направлении (влево или вправо от оси сосуда) на 1 см и снова опускают до соприкосновения её острия со свободной поверхностью, берут отсчет по нониусу с точностью до 0,1 мм.
Рис. 4.3. Схема опытной установки ГД-2:
- 1 – корпус; 2 – цилиндрический сосуд; 5 – измерительная игла;
- 4,8 – рукояти, 5,6 – шкалы; 7 – направляющая, 9 – панель; 10 – тумблер; 11 – лампочка; 12 – индикатор; 13 – регулятор; 14 – штанга
Аналогичные измерения проводят для ряда других точек, расположенных вдоль радиуса сосуда (7…8 точек).
Регулятором (13) изменяют частоту вращения сосуда с жидкостью и повторяют все измерения.
По окончании измерений необходимо выключить тумблер (10). Данные измерений заносят в табл. 4.1.
Таблица 4.1
Измерение координат свободной поверхности
№ ТОЧКИ | Отсчет по горизонтальной шкале, см | Отсчёт по вертикальной шкале, см | ||
iii = | ГЬ = | п, = | ГЬ = | |
Обработки результатов измерений
С помощью экспериментально полученных данных вычисляют zoon при различных частотах вращения сосуда П и п2 относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности как разность отсчетов по вертикальной шкале, соответствующих данной точке свободной поверхности и положению иглы в центре сосуда.
По формуле (4.4) вычисляют теоретические значения z0Teop поверхности относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности, при этом берется гтеор = гоп.
Расхождение в процентах между величинами z0on и z(trcop подсчитывают по формуле
Результаты вычислений заносят в табл. 4.2.
Таблица 4.2
Определение отметок свободной поверхности
№ точки | Расстояние от точки до оси вращения г, м | Угловая скорость вращения сосуда to, рад/с | Отметки свободной поверхности, м | Расхождение между zoom и ^Отсор» /о | |||
Пэ = | Пэ = | ||||||
ZO on | ZO тсор | Z ом | Z() тсор | ||||
П1 = Пэ = | и с И с | Пэ = П2 = | |||||
На графике в масштабе 1:2 строят теоретические и экспериментальные кривые свободной поверхности жидкости z0on= f(r) и z() теор = f(r), используя карандаши различного цвета.
По формуле (4.4) и величине z0on третьей серии измерений вычисляют угловую скорость вращения сосуда со, а затем из зависимости
вычисляют частоту вращения п сосуда с жидкостью.
- 1. Какие силы действуют на жидкость при абсолютном покое?
- 2. Какие силы действуют на жидкость в случае её относительного покоя?
- 3. Какую форму принимает свободная поверхность жидкости в случае абсолютного и относительного покоя жидкости?
- 4. Как определить глубину параболоида вращения?
- 5. От чего зависит глубина параболоида вращения?
- 6. Каково уравнение поверхности равного давления в случае абсолютного и относительного покоя жидкости?
- 7. Запишите уравнение равновесия жидкости для абсолютного и относительного покоя (уравнение Эйлера) и объясните смысл входящих в него величин.
- 8. Запишите уравнение свободной поверхности жидкости для случая равномерного вращения цилиндрического сосуда вокруг собственной вертикальной оси?
- 9. Как определить угловую скорость вращения сосуда?
Источник
Цель работы –
экспериментальное установление формы
свободной поверхности жидкости в круглом
цилиндрическом сосуде, вращающемся с
постоянной угловой скоростью вокруг
собственной вертикальной оси, и
аппроксимация (приближение) формы
свободной поверхности, полученной из
опыта, теоретическим параболоидом
вращения.
Содержание работы
– изучение поведения тяжелой капельной
жидкости, находящейся во вращающемся
сосуде, с сопоставлением расчетных и
экспериментальных результатов.
Теоретические основы
Пусть
открытый вертикальный прямой круглый
цилиндрический сосуд с жидкостью
вращается вокруг своей оси с постоянной
угловой скоростью .
Жидкость, постепенно увлекаясь во
вращение вследствие вязкости, в
установленном режиме вращается вместе
с сосудом, как единое целое с той же
угловой скоростью ,
т.е. находится в состоянии покоя
относительно стенок сосуда. Это состояние
поддерживается равновесием сил
гидростатического давления (Р),
тяжести (g)
и центробежной силы инерции (![]() ),
),
действующих на каждую частицу жидкости
(сила вязкого трения в установившемся
состоянии относительного покоя
отсутствует). Из уравнения равновесия
Эйлера получается следующее распределение
давлений в жидкости
![]() ,
,
где
z
– ордината жидкой частицы, отсчитанная
по вертикали вверх от самой нижней точки
свободной поверхности;
r
– расстояние до частицы по горизонтали
от оси вращения;
–
угловая скорость вращения;
18
– плотность жидкости;
g
– ускорение силы тяжести (g
= 9,81
![]() );
);
Р
– давление в жидкой частице с координатами
z
и r.
Из приведенного
уравнения при Р
= const
(dP = 0)
получаются уравнения поверхностей
равного давления, образующих семейство
осесимметричных параболоидов вращения
с общей осью z.
В частности, при
![]()
получается уравнение свободной
поверхности, любое меридиональное
сечение которой представляет собой
параболу с вертикальной осью симметрии
![]() .
.
Как видно из
последнего уравнения, форма свободной
поверхности определяется только
параметрами
![]()
и r
и не зависит от рода используемой
жидкости.
Лабораторная
установка (рис. 9) состоит из открытого
круглого цилиндрического сосуда 1, днище
которого закреплено на вертикальном
валу 2, расположенном на оси симметрии
z
сосуда. Сосуд, наполненный примерно на
половину водой, приводится во вращение
с постоянным числом n
оборотов в минуту электродвигателем 3
через передачу 4. Определение координат
свободной поверхности 5 производится
с помощью координатника 6, закрепленного
на неподвижной раме 7 прибора. По
горизонтальным направляющим с
миллиметровой шкалой 8 с помощью винта
9 перемещается каретка с измерительной
иглой 10. Игла может перемещаться по
вертикальным направляющим с миллиметровой
шкалой 11 и фиксироваться винтом 12. Для
отсчета горизонтальных и вертикальных
координат на каретке и игле нанесены
риски.
При математической
обработке наблюдений вычисляются
расстояния
![]()
от оси вращения до симметрично
расположенных левых
и правых точек с номером i
по формуле
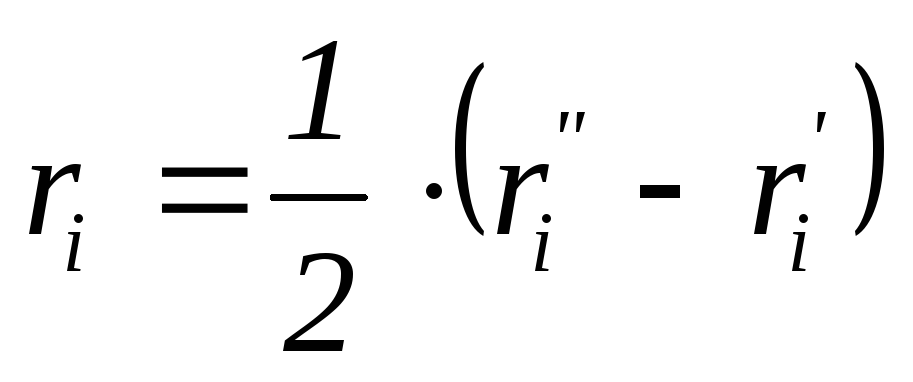 .
.
19
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
