Эпюра давления на дно сосуда

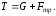
Эта статья описывает, как правильно строить эпюру гидростатического давления. Этот материал полезен в первую очередь студентам, изучающим курс механики жидкости и газа (гидравлики).

Эпюра давления — это графическое изображение распределения гидростатического давления по стенке или по длине какого-либо контура

Как правило, эпюру давления строят от избыточного гидростатического давления. О видах давления подробно можно прочитать в этойстатье сайта Проводу.рф.

Построение эпюры давления заключается в расчете давления в различных точках контура (стенки), на который давит жидкость, в и откладывании этой величины давления в виде отрезка перпендикулярно контуру в определенном масштабе.

Расчет давления выполняют по формуле (основное уравнение гидростатики):

Эпюра давления на дно сосуда Здесь Px — избыточное давление (превышение над атмосферным), Па; ρ — плотность жидкости, кг/м3 ; g — ускорение свободного падения, g = 9,81 м/с2 ; h — глубина (высота столба жидкости над точной), м.

Далее рассмотрим различные случаи, связанные с построением эпюры гидростатического давления — от самого простого к наиболее трудному.

1 Эпюра давления жидкости на вертикальную стенку

Когда мы имеем дело с вертикальной плоской стенкой, нам бессмысленно считать давление в каждой точке, достаточно всего в двух: сверху в месте, где находится свободная поверхность (уровень) жидкости — точка 1, и снизу на дне, точка 2.

В данном случае избыточное давление в точке 1: p1 = 0 Па,

Избыточное давление в точке 2: p2 = ρ g H.

2 Эпюра давления на наклонную стенку

Практически ничем не отличается случай, когда рассматривается давление на наклонную стенку. Значение давления, рассчитанное по основному уравнению гидростатики, откладывается перпендикулярно стенке. Опять же достаточно определить давление в двух точках — сверху и снизу. Сверху, если резервуар открытый, до давление будет равно 0 Па. Снизу на дне — ρ g h.

3 Эпюра давления на наклонную стенку + на поверхности жидкости есть избыточное давление

Если на поверхности жидкости есть избыточное давление p0, то его величина, согласно основному уравнению гидростатики, будет добавлена во всех точках наклонной стенки. Тогда к эпюре-треугольнику добавится еще прямоугольник, ширина которого равна p0 .

Итоговая эпюра будет иметь форму трапеции.

4 Эпюра давления на криволинейную поверхность

Построение эпюры давления на криволинейную поверхность требует вычисления давления во многих точках этой поверхности, а значения давления откладываются по нормали к соответствующим точкам. То есть нужно выбрать несколько точек ( сколько — зависит от масштаба схемы, но чтобы была возможность изобразить по этим точкам именно криволинейную, а не ломанную линию), и вычислить в них давление по основному уравнению гидростатики.

5 Эпюра двухстороннего давления, с двух сторон щита одинаковая жидкость

При наличии жидкости с двух сторон щита, необходимо строить отдельно две эпюры гидростатического давления (два треугольника — слева и справа). После этого эпюра справа вычитается из большой эпюры слева, и остается трапеция, которая учитывает давление и слева, и справа.

Т.е. наличие уровня жидкости справа частично компенсирует то давление, которое создает жидкость слева.

6 Эпюра двухстороннего давления, когда с двух сторон щита находятся жидкости с разными плотностями

Эпюра давления на дно сосуда

Здесь синим цветом показана эпюра для жидкости справа, которая «вырезается» из эпюры для жидкости слева. Т.е. во всех точках щита в той части, где вода находится с двух сторон, вычисляется разница давлений слева и справа. Эта разница и позволит построить результирующую эпюру давления (показана черным цветом).

7 Эпюра давления жидкости на стенку сложной формы, содержащую вогнутую область

Эпюра давления на дно сосуда

Принципиально данная задача ничем не отличается от предыдущих: в каждой точке контура мы вычисляем давление и в масштабе откладываем его значение по нормали к контуру.

С точки зрения графического построения, здесь возможно поступить следующим образом: сначала построить эпюру-треугольник. Он показывает, как увеличивается давление с глубиной. При этом он позволяет нам в виде отрезка получить давление в каждой точке. И дальше останется только перенести эти отрезки в соответствующие точки нашего контура. С верхней и нижней стенками при этом не должно возникнуть проблем. Эпюру для вогнутой области строим по принципу случая 4. Удобнее всего будет наметить несколько точек на этом вогнутом контуре, затем провести к ним касательные линии, и отложить значение давления, посчитанное заранее или взятое из треугольника в виде отрезка, перпендикулярно этим касательным. Эффект достигнут.

Источник

Графическое
изображение распределения гидростатического
давления по поверхности тела, погруженного
в жидкость, называется эпюрой
гидростатического
давления.

При
построении эпюр гидростатического
давления используются два основных
принципа, вытекающие из свойств
гидростатического давления:

гидростатическое
давление является векторной
величиной.
Вектор гидростатического давления
направлен по нормали к поверхности
тела, погруженного в жидкость;
модуль
вектора
гидростатического давления определяется
по уравнению (1.11) для построения эпюр
абсолютного давления и (1.12) для построения
эпюр избыточного гидростатического
давления.

Для плоских
прямоугольных стенок эпюры избыточного
и абсолютного гидростатического давления
имеют вид, представленный на рис. 1.14
и
рис. 1.15.

Равнодействующая
элементарных сил гидростатического
давления, действующих на какую-либо
стенку, называется
силой гидростатического давления.

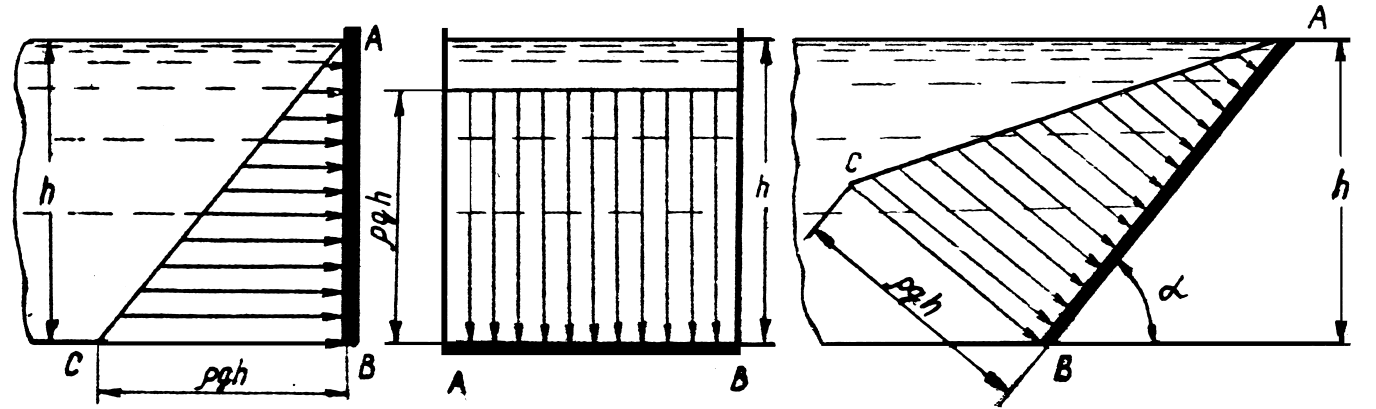
Эпюра давления на дно сосуда

Рис.
1.14

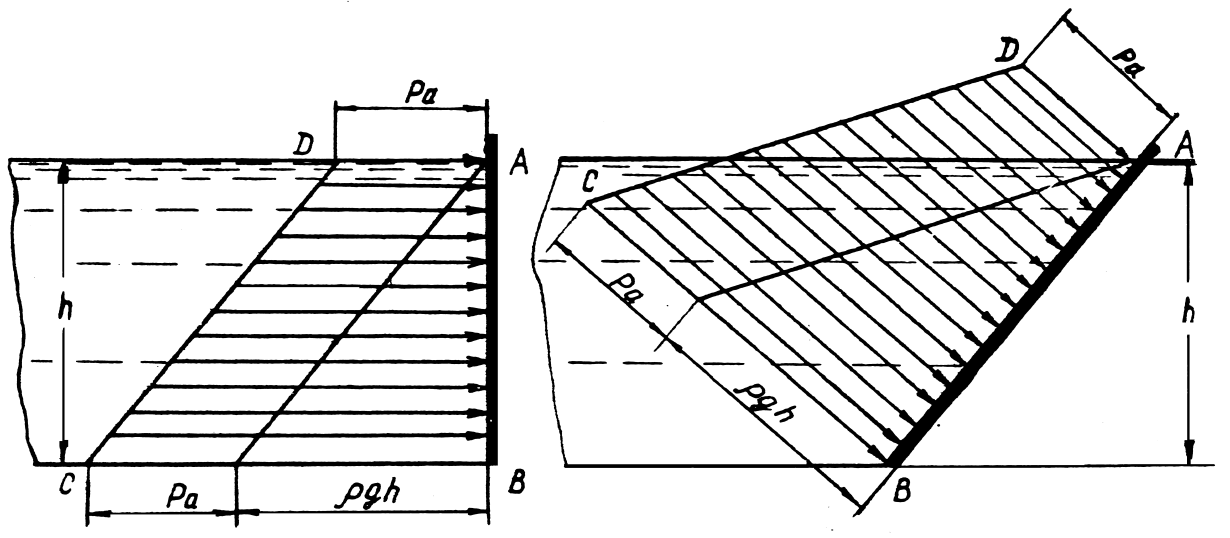
Эпюра давления на дно сосуда

Рис.
1.15

Сила
гидростатического давления на площадку
определяется произведением её площади
на гидростатическое давление в центре
тяжести площадки (рис. 1.16).

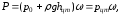Эпюра давления на дно сосуда (1.15)

где
P
– сила гидростатического давления, Н;

hцт
– глубина погружения центра тяжести
фигуры, м;

pцт
– гидростатическое давление в центре
тяжести фигуры, Па.

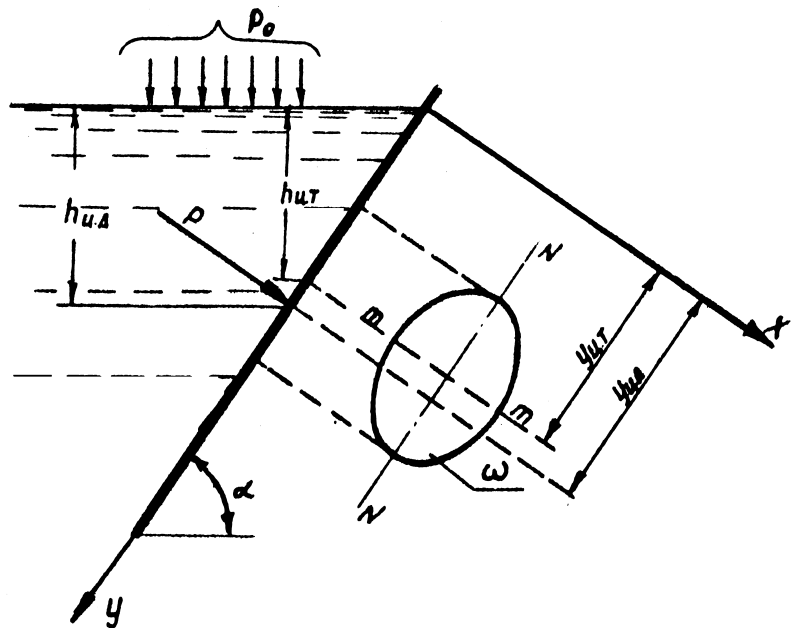
Эпюра давления на дно сосуда

Рис.
1.16

Точка
приложения силы Р
называется центром давления. Координата
центра давления
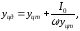Эпюра давления на дно сосуда для симметричных относительно осиN–N
фигур определится из уравнения

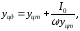Эпюра давления на дно сосуда (1.16)

где
I
– момент инерции площади 
относительно оси m–m.

Значения
I

и yцт
для некоторых фигур приведены в
приложении 5.

Сила
гидростатического давления Р
может быть определена графическим
способом как произведение площади эпюры
гидростатического давления на ширину
стенки.

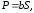Эпюра давления на дно сосуда (1.17)

где
S
– площадь эпюры гидростатического
давления, Н/м;

b
– ширина стенки, м.

Сила
давления проходит через центр тяжести
эпюры гидростатического давления и
направлена по нормали к поверхности.

Сила
избыточного гидростатического давления
для плоских прямоугольных стенок,
изображенных на рис. 1.14, может быть
определена по формулам:

Вертикальная
стенка

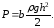Эпюра давления на дно сосуда (1.18)

Горизонтальная
стенка

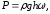Эпюра давления на дно сосуда (1.19)

где

– площадь дна, м2.

Наклонная
стенка

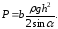Эпюра давления на дно сосуда (1.20)

Закон Архимеда

Сила,
с которой жидкость действует на
погруженное в неё тело, равна весу
жидкости в объёме погруженного тела и
направлена вертикально вверх.

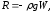Эпюра давления на дно сосуда (1.21)

где
R–
выталкивающая сила, Н;

 – плотность
жидкости, кг/м3;

W
– объём погруженного тела, м3.

Задачи

Определить
силу избыточного гидростатического
давления на вертикальную стенку
водонапорного бака шириной 5 м.
В баке, размеры которого в плане
составляют 45 м,
находится 35 м3
воды. Построить эпюру избыточного
гидростатического давления на эту
стенку.
Определить
силу избыточного гидростатического
давления на за-слонку, закрывающую
отверстие в стенке резервуара (рис.
1.17). Резервуар заполнен нефтью 
= 850 кг/м3.
Размеры заслонки 1010 см.
Высота слоя нефти до начала заслонки
6 м.
Построить эпюру избыточного
гидростатического давления на заслонку.

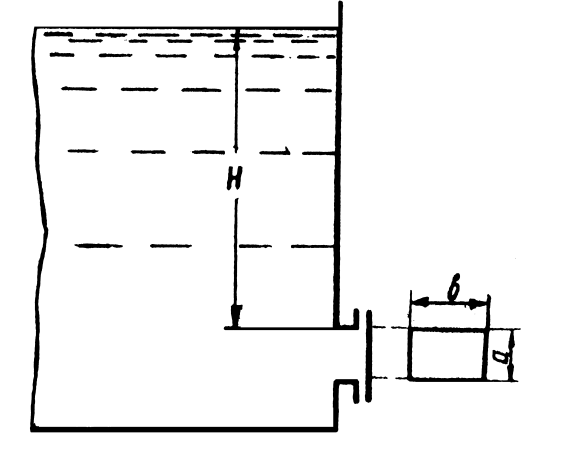
Эпюра давления на дно сосуда

Рис.
1.17

Решение.
Силу избыточного гидростатического
давления определим графическим способом
как произведение площади эпюры избыточного
гидростатического давления (рис. 1.17б)
на ширину заслонки

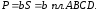
Эпюра давления на дно сосуда

Эпюра
избыточного гидростатического давления
имеет форму трапеции, площадь которой
определяется как произведение полусуммы
оснований на высоту

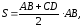
Эпюра давления на дно сосуда

где
АВ
= gh1
= 8509,816
= 50,03103 Па
–
гидростатическое давление
в точке
А;

СD
= gh2
= 8509,816,1
= 50,86103 Па
– гидростатическое давление
в точке
В;

ВС
= h2-h1
= 6,1-6,0 = 0,1 м
– высота трапеции.

Тогда

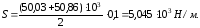
Эпюра давления на дно сосуда

Сила
избыточного гидростатического давления

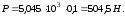
Эпюра давления на дно сосуда

Определить
силу избыточного гидростатического
давления на заслонку размерами a
= 15 см,
b
= 20 см
(рис. 1.17а), закрывающую отверстие
в
стенке резервуара с бензином плотностью

= 700 кг/м3.
Высота слоя бензина до начала заслонки
7 м.
Построить эпюру избыточного
гидростатического давления.
Определить
силу избыточного гидростатического
давления на откос пожарного водоёма
(рис. 1.18) шириной 8 м, если глубина
воды в водоеме 3,5м, угол наклона
откоса составляет 45.
Построить эпюру избыточного
гидростатического давления.

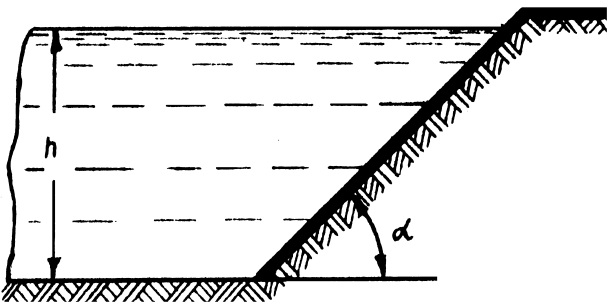
Эпюра давления на дно сосуда

Рис.
1.18

Канал
шириной 4 м
и глубиной 3 м
перегорожен щитом прямоугольной формы
(рис. 1.19). Определить силу тяги, необходимую
для подъ-
ёма щита весом 15 кН,
если коэффициент трения щита о
поверхность пазов составляет 0,5.

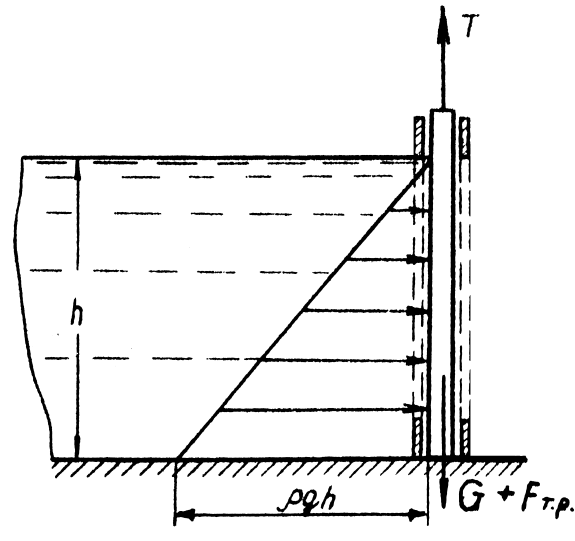
Эпюра давления на дно сосуда

Рис.
1.19

Решение.
Сила тяги может быть определена как
сумма веса щита G
и силы трения щита о поверхность пазов
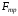
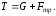
Эпюра давления на дно сосуда

Эпюра давления на дно сосуда

Сила
трения определяется как произведение
силы нормального (в данном случае
гидростатического) давления на коэффициент
трения.

Силу
избыточного гидростатического давления
определим графическим способом как
произведение эпюры избыточного
гидростатического давления на ширину
стенки

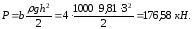
Эпюра давления на дно сосуда

Тогда

Эпюра давления на дно сосуда

Определить
силу тяги, необходимую для подъёма
щита весом 10 кН,
который перегораживает канал глубиной
2 м.
Ширина щита 3 м.
Коэффициент трения щита о поверхность
пазов 0,4 (рис. 1.19).
Определить
силу избыточного гидростатического
давления и центр давления на наклонную
крышку, которая закрывает круглую
трубу диаметром 1 м
водовыпуска из пожарного водоема (рис.
1.20). Угол наклона крыши 
= 60.
Ось водовыпуска находится на глубине
Н
= 2 м.

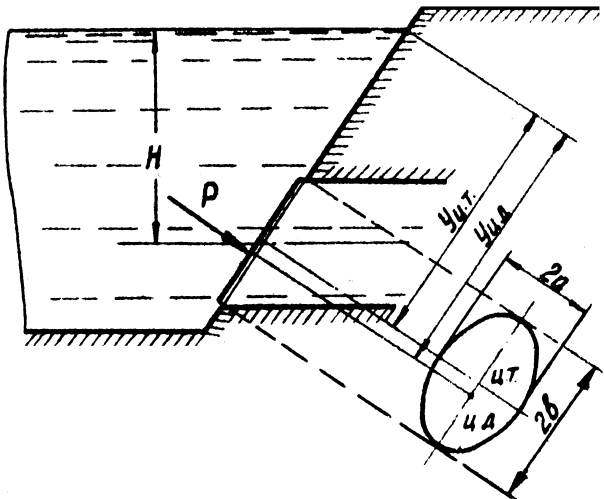
Эпюра давления на дно сосуда

Рис.
1.20

Решение.
Силу давления на крышку определим
аналитическим способом как произведение
гидростатического давления в центре
тяжести крышки на её площадь:

Эпюра давления на дно сосуда

Площадь
крышки, имеющей форму эллипса

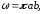
Эпюра давления на дно сосуда

где
а
и b
– полуоси эллипса.

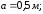
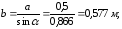
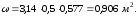
Эпюра давления на дно сосуда

Тогда

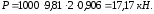
Эпюра давления на дно сосуда

Расстояние
до центра тяжести эллипса

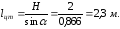
Эпюра давления на дно сосуда

Координата
центра давления

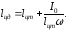
Эпюра давления на дно сосуда

Момент
инерции эллипса

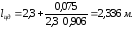
Эпюра давления на дно сосуда

Тогда

Эпюра давления на дно сосуда

Определить
силу избыточного гидростатического
давления и центр давления на наклонную
крышку (рис. 1.21), если:

а)
H
= 3 м;
d
= 0,8 м; 
= 45;

б)
H
= 3,5 м;
d
= 0,9 м; 
= 30;

в)
H
= 4 м;
d
= 1,0 м; 
= 50.

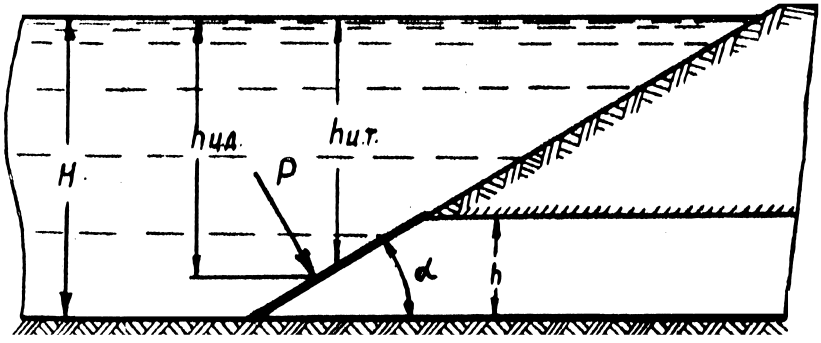
Эпюра давления на дно сосуда

Рис.
1.21

Определить
силу избыточного гидростатического
давления и центр давления на плоский
затвор (рис. 1.21), которым перекрывается
водовыпуск пожарного водоема. Глубина
водоема 3 м,
высота прямоугольного канала водовыпуска
h
= 1 м,
ширина b
= 0,8 м,
угол наклона затвора к горизонту 
= 30.
Построить эпюру избыточного
гидростатического давления на затвор.
Определить
силу избыточного гидростатического
давления на промежуточную вертикальную
стенку пожарного резервуара шириной
6 м.
Стенка разделяет резервуар на два
отсека (рис. 1.22), уровень воды в первом
отсеке 2 м,
во втором – 1 м.
Построить эпюру избыточного
гидростатического давления.

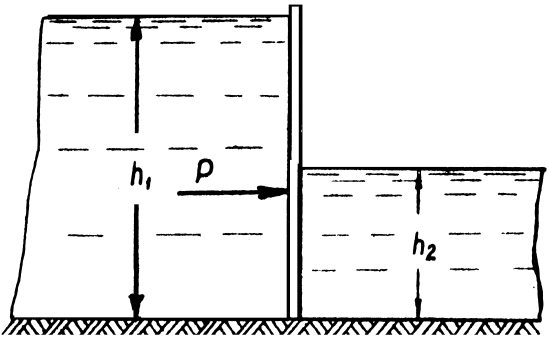
Эпюра давления на дно сосуда

Рис.
1.22

Для
приведённых на рисунке 1.23 плоских
прямоугольных фигур построить эпюры
избыточного гидростатического давления.

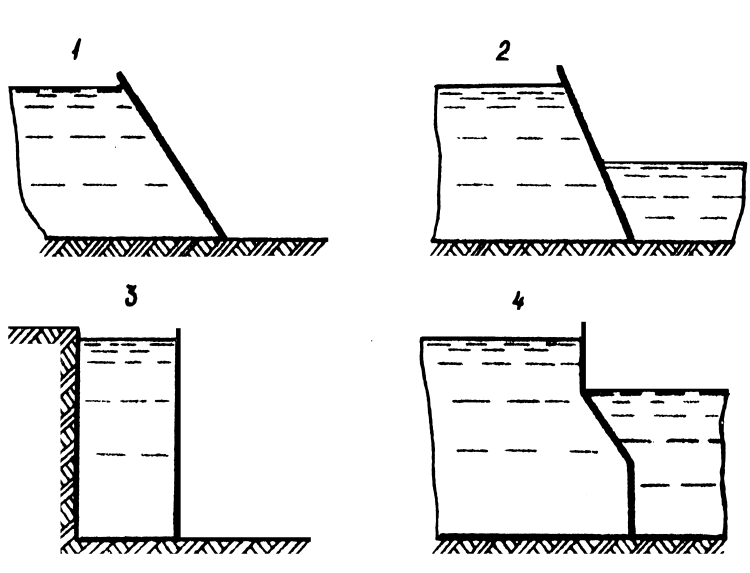
Эпюра давления на дно сосуда

Рис. 1.23

Для
приведённых на рисунке 1.24 криволинейных
стенок построить эпюры избыточного
гидростатического давления.

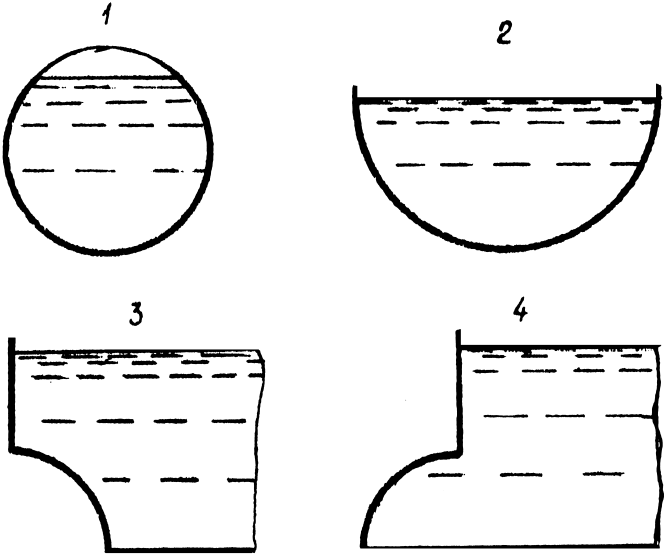
Эпюра давления на дно сосуда

Рис. 1.24

Определить
минимальный диаметр шарового поплавка,
который обеспечивает автоматическое
закрытие клапана при наполнении
резервуара (рис. 1.25), если а
= 120 мм,
b
= 600 мм.
Вода поступает в резервуар под давлением
p
= 1,5105 Па
по трубе диаметром 150 мм.
Массой рычага, клапана и поплавка
пренебречь.

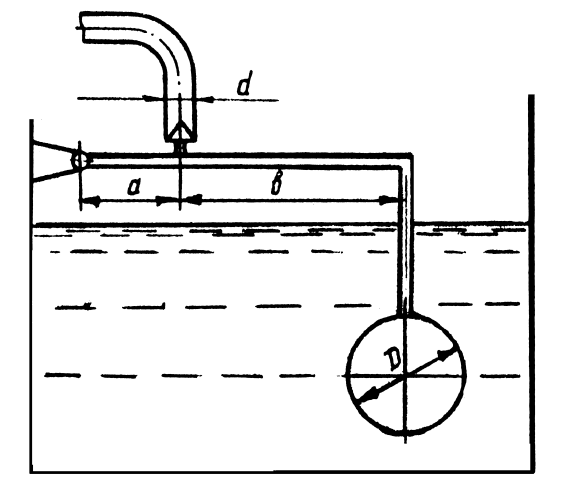
Эпюра давления на дно сосуда

Рис. 1.25

Плотность
жидкости измеряется при помощи ареометра
(рис. 1.26). Внешний диаметр трубки
20 мм,
диаметр шарика с дробью 30 мм,
масса ареометра 0,060 кг.
Определить плотность жидкости, если
глубина погружения в ней ареометра
составляет h
= 150 мм.

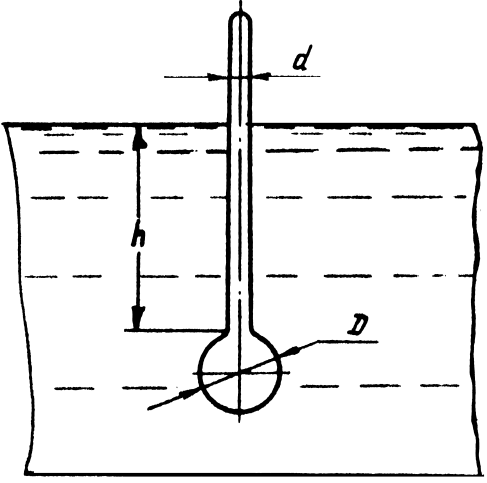
Эпюра давления на дно сосуда

Рис. 1.26

Определить
глубину погружения ареометра в жидкость
плотностью 800 кг/м3
(рис. 1.26), если внешний диаметр трубки
25 мм,
диаметр шарика с дробью 40 мм,
масса ареометра 0,080 кг.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Для решения многих практических задач приходится строить эпюры гидростатического давления, которые представляют собой графические изображения распределения гидростатического давления на плоские прямоугольные поверхности. Эпюра помогает уяснить характер неравномерности передаваемого от жидкости на стенку давления.

Рассмотрим случай определения гидростатического давления на плоскую вертикальную стенку АВ, шириной СВ, на которую давит жидкость с плотностью ρ и высотой h (рисунок 5).

Для этого воспользуемся основным уравнением гидростатики

Рабс = ρqh + Ра

Это уравнение гидростатического давления по глубине и является уравнением прямой.

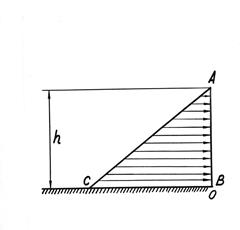Рисунок 5

Следовательно, для построения эпюры гидростатического давления, действующего на стенку, необходимо знать две точки: гидростатическое давление на поверхность жидкости и у днища резервуара.

Избыточное давление на поверхности жидкости равно нулю, т.к.

Рабс = Ра

У днища резервуара избыточное давление

Ризб = ρqh

Приняв за начало координат точку 0 и отложив в выбранном масштабе из точки 0 величину

Ризб = ρqh

перпендикулярно стенке АВ (согласно первому свойству гидростатического давления) соединяем полученную точку С с точкой А прямой линией. Треугольник АВС называют эпюрой избыточного давления на плоскую вертикальную стенку.

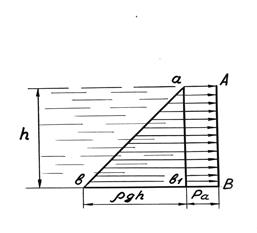Эпюра абсолютного гидростатического давления на стенку АВ изобразится трапецией АавВ (рисунок 6), состоящей из прямоугольника Аав1В, ширина которого Аа и Вв1, выраженная в масштабе, представляет собой атмосферное

Рисунок 6

давление и треугольника авв1, представляющего характер изменения избыточного давления ρqh по глубине резервуара, выраженного в том же масштабе, что и атмосферное давление.

Так как атмосферное давление оказывает воздействие на открытую свободную поверхность жидкости и на стенки сосуда (резервуара) с внешней стороны, то действие его уравновешивается. Поэтому в технических расчетах чаще всего определяют избыточное гидростатическое давление

Ризб = ρqh

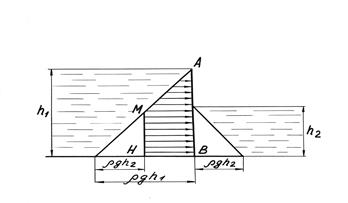Рассмотрим эпюру избыточного гидростатического давления для вертикальной плоскости АВ, подверженной действию жидкости с двух сторон (рисунок 7).

Рисунок 7

В данном случае на стенку АВ будут действовать параллельные и противоположно направленные силы гидростатического давления.

Поэтому силы, действующие справа налево, будут вычитаться из сил, действующих слева направо.

Получающаяся в результате эпюра представляет собой вертикальную трапецию.

Эпюра гидростатического давления на горизонтальное плоское днище резервуара представляет собой вертикальный прямоугольник (рисунок 8), так как при постоянной глубине избыточное гидростатическое давление на днище является постоянным.

Pизб= ρqhωдн

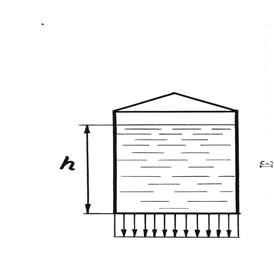Рисунок 8

В случае, когда сосуд имеет наклонную стенку, составляющую с горизонтальной плоскостью некоторый угол α, эпюра избыточного гидростатического давления представляет собой прямоугольный треугольник (рис.9) АbВ, в котором отрезки, изображающие давления, наклонены к горизонтальной плоскости под углом 900.

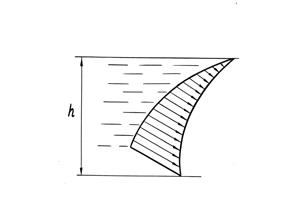Рисунок 9

На рисунке 10 изображены три сосуда различной формы, заполненные одинаковой жидкостью на одинаковую высоту h и во всех трёх сосудах площадь дна одинакова.

В каком сосуде будет больше сила гидростатического давления на дно сосуда?

(Проблемный вопрос).

В лекции отмечалось, что, если стенка расположена горизонтально, т.е. представляет собой не боковую стенку, а горизонтальное дно резервуара, то суммарное давление на дно резервуара определится по формуле

Ризб= ρqhω

где h—глубина жидкости в резервуаре.

Следовательно, давление на дно резервуара (сосуда) зависит не от формы объёма жидкости в нём, а только от площади дна и глубины жидкости в сосуде. Поэтому для сосудов разной формы (рисунок 12), заполненных одной и той же жидкостью до одного и того же уровня h и имеющих одинаковую площадь дна, сила полного гидростатического давления на дно будет одинакова.

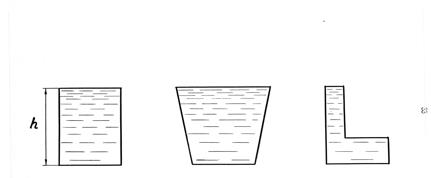Рис.12

Это явление известно под названием гидростатического парадокса.

Оно было впервые открыто итальянским физиком Галлилеем (1564-1642гг.) Это явление также известно как второй закон французского физика Паскаля (1623-1662гг.).

Источник

Ïîíÿòèå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ, îñíîâíîå óðàâíåíèå ãèäðîñòàòèêè. Îñíîâíûå âèäû äàâëåíèé: àáñîëþòíîå, àòìîñôåðíîå, èçáûòî÷íîå, âàêóóììåòðè÷åñêîå. Ïðèìåð îïðåäåëåíèÿ ãèäðîñòàòè÷åñêîãî (èçáûòî÷íîãî) äàâëåíèÿ è ïîñòðîåíèÿ ýïþðû íà äíî è ñòåíêè ñîñóäîâ.

Îòïðàâèòü ñâîþ õîðîøóþ ðàáîòó â áàçó çíàíèé ïðîñòî. Èñïîëüçóéòå ôîðìó, ðàñïîëîæåííóþ íèæå

Ñòóäåíòû, àñïèðàíòû, ìîëîäûå ó÷åíûå, èñïîëüçóþùèå áàçó çíàíèé â ñâîåé ó÷åáå è ðàáîòå, áóäóò âàì î÷åíü áëàãîäàðíû.

Ðàçìåùåíî íà https://www.allbest.ru/

ÐÃÐ 1

ïî ãèäðàâëèêå, ãèäðîëîãèè è ãèäðîìåòðèè äëÿ ñòóäåíòîâ ñòðîèòåëüíîé ñïåöèàëüíîñòè âñåõ ôîðì îáó÷åíèÿ

Òåìà: ïîñòðîåíèå ýïþð ãèäðîñòàòè÷åñêîãî äàâëåíèÿ íà äíî è ñòåíêè ñìåæíûõ ñîñóäîâ

1. Îñíîâíûå ñâåäåíèÿ è îïðåäåëåíèÿ

Ãèäðîñòàòè÷åñêîå äàâëåíèå – ýòî äàâëåíèå, âîçíèêàþùåå â ïîêîÿùåéñÿ æèäêîñòè ïîä äåéñòâèåì âíåøíèõ ñèë.

Åäèíèöû èçìåðåíèÿ äàâëåíèÿ:

1 áàð = 1,02 àò = 0,1 ÌÏà = 750 ìì ðò. ñò. = 10,2 ì âîä. ñò.

Îñíîâíîå óðàâíåíèå ãèäðîñòàòèêè

Ð = Ðàò + ñgH,

ãäå Ð – àáñîëþòíîå äàâëåíèå â äàííîé òî÷êå, Ïà; Ðàò – àòìîñôåðíîå äàâëåíèå íà ïîâåðõíîñòè, Ïà; ñ – ïëîòíîñòü æèäêîñòè, êã/ì3; g – óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ, ì/ñ2; Í – âûñîòà ñòîëáà îäíîðîäíîé æèäêîñòè, ì.

Ðàçëè÷àþò ñëåäóþùèå âèäû äàâëåíèé: àáñîëþòíîå, àòìîñôåðíîå (áàðîìåòðè÷åñêîå), èçáûòî÷íîå (ìàíîìåòðè÷åñêîå) è âàêóóììåòðè÷åñêîå (ðàçðåæåíèå). ãèäðîñòàòè÷åñêèé äàâëåíèå èçáûòî÷íûé ñîñóä

Àòìîñôåðíîå äàâëåíèå çàâèñèò îò ïîëîæåíèÿ ìåñòà, åãî âûñîòû íàä óðîâíåì ìîðÿ. Äëÿ ã. Êàðàãàíäû Ðàò=715 ìì ðò. ñò.

Åñëè ïîâåðõíîñòü æèäêîñòè ñîïðèêàñàåòñÿ ñ àòìîñôåðîé, òî Ð = Ðàò.

2. Ðàñ÷åòíàÿ ñõåìà

Òàáëèöà 1 Âàðèàíò çàäàíèÿ

¹ âàðèàíòà	Í	Í	Í	Í	Í	Í	Íàçâàíèå æèäêîñòè, ïëîòíîñòü (êã/ì3)
Âûñîòà ñëîÿ, ì, Ãëóáèíà	Æèäêîñòü 1	Æèäêîñòü 2	Æèäêîñòü 3	Æèäêîñòü 4	Æèäêîñòü 5	Æèäêîñòü 6
1	2	3	4	5	6	7	8	9	10	11	12	13
1	3	10	8	5	7	7	Ðòóòü, (13340)	Âîäà, (1000)	Áåíçèí, (720)	Ðòóòü, (13340)	Äåãîòü, (1100)	Ãàçîëèí, (750)
2	2,5	8	10	4	10	6	Ðòóòü, (13340)	Ìàçóò, (900)	Ìàøèííîå ìàñëî, (910)	Ðòóòü, (13340)	Êðåîçîòîâîå ìàñëî, (1070)	Ñêèïèäàð, (871)
3	4	6	11	1,5	15	7	Ðòóòü, (13340)	Äåãîòü, (1100)	Àëêîãîëü áåçâîäíûé, (790)	Ðòóòü, (13340)	NaCL, (1210)	Êåðîñèí, (845)
4	3	8	10	2	12	4	Ðòóòü, (13340)	Âîäà, (1000)	Áåíçèí, (720)	Ðòóòü, (13340)	Äåãîòü, (1100)	Ìàçóò, (850)
5	5	7	8	2	10	7	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	Âîäà, (1000)	Ðòóòü, (13340)	Äåãîòü, (1100)	Ìàøèííîå ìàñëî, (910)
6	3,5	10	6	7	5	11	Ðòóòü, (13340)	Âîäà, (1000)	Àëêîãîëü áåçâîäíûé, (790)	Ðòóòü, (13340)	NaCl, (1210)	Êåðîñèí, (900)
7	4,5	8	6	2	13	6	Ðòóòü, (13340)	Öèëèíäðè÷åñêîå ìàñëî, (915)	Áåíçèí, (?50)	Ðòóòü, (13340)	Ãëèíÿíîå òåñòî, (1450)	Ìàçóò, (920)
8	1,5	7	5	4	10	5	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî 1,5, (1260)	Ìàçóò, (880)	Ðòóòü, (13340)	Êðåîçîòîâîå ìàñëî, (1070)	Ìàøèííîå ìàñëî, (910)
9	4	9	7	3	4	12	Ðòóòü, (13340)	Òðåïåëüíîå òåñòî, (1370)	Âîäà, (1000)	Ðòóòü, (13340)	NaCL, (1210)	Êåðîñèí, (900)
10	3	5	7	5	10	8	Ðòóòü, (13340)	Äåãîòü, (1100)	Ãàçîëèí, (750)	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	Ìàçóò, (900)
11	2	8	10	4	9	7	Ðòóòü, (13340)	Âîäà, (1000)	Áåíçèí, (720)	Ðòóòü, (13340)	Ìàçóò, (900)	Ãàçîëèí, (750)
12	5	10	7	2	7	8	Ðòóòü, (13340)	Ãëèíÿíîå òåñòî, (1450)	Âîäà, (1000)	Ðòóòü, (13340)	Äåãîòü, (1100)	Ñêèïèäàð, (871)
13	3	5	7	7	3	8	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	Êðåîçîòîâîå ìàñëî, (1070)	Ðòóòü, (13340)	Ãëèíÿíîå òåñòî, (1450)	NaCL, (1210)
14	2,5	10	6	4	8	10	Ðòóòü, (13340)	Òðåïåëüíîå òåñòî, (1370)	Àëêîãîëü áåçâîäíûé, (790)	Ðòóòü, (13340)	NaCL, (1210)	Ìàøèííîå ìàñëî, (910)
15	4	15	2	3	6	11	Ðòóòü, (13340)	Äåãîòü, (1100)	Âîäà, (1000)	Ðòóòü, (13340)	Êðåîçîòîâîå ìàñëî, (1070)	Ñêèïèäàð, (871)
16	3	12	4	4	//	6	Ðòóòü, (13340)	Âîäà, (1000)	Ìàçóò, (900)	Ðòóòü, (13340)	Äåãîòü, (1100)	Êåðîñèí, (900)
17	5	10	7	2	7	8	Ðòóòü, (13340)	Êåðîñèí, (900)	Àëêîãîëü áåçâîäíûé, (790)	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	Âîäà, (1000)
18	0,5	3,5	2,5	1	4	2	Ðòóòü, (13340)	Âîäà, (1000)	Öèëèíäðè÷åñêîå ìàñëî, (915)	Ðòóòü, (13340)	Ìàøèííîå ìàñëî, (910)	Àëêîãîëü áåçâîäíûé, (790)
19	1	2	4	1,5	3	2	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	Äåãîòü, (1100)	Ðòóòü, (13340)	Êåðîñèí, (900)	Áåíçèí, (720)
20	1,5	2	4	0,5	2	5	Ðòóòü, (13340)	Ãëèíÿíîå òåñòî, (1450)	Âîäà, (1000)	Ðòóòü, (13340)	Ìàçóò, (900)	Áåíçèí, (720)
21	4	7	3	1	9	3	Ðòóòü, (13340)	Âîäà, (1000)	Àëêîãîëü áåçâîäíûé, (790)	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	NaCL, (1210)
22	3	5	8	2	9	4	Ðòóòü, (13340)	Òðåïåëüíîå òåñòî, (1370)	NaCL, (1210)	Ðòóòü, (13340)	Âîäà, (1000)	Ìàçóò, (900)
23	2,5	5,5	7	3	5,5	9	Ðòóòü, (13340)	Êåðîñèí, (900)	Ñêèïèäàð, (871)	Ðòóòü, (13340)	Òðåïåëüíîå òåñòî, (1370)	Áåíçèí, (720)
24	1	3	7	3	5	5	Ðòóòü, (13340)	Âîäà, (1000)	Ìàçóò, (900)	Ðòóòü, (13340)	Äåãîòü, (1100)	Àëêîãîëü áåçâîäíûé, (790)
25	1,5	7	8	5	3	7	Ðòóòü, (13340)	Èçâåñòêîâîå òåñòî, (1360)	Áåíçèí, (720)	Ðòóòü, (13340)	Âîäà, (1000)	Ñêèïèäàð, (871)

3. Ïðèìåð ðåøåíèÿ

Èñõîäíûå äàííûå:

Í1(ðòóòü) = 3 ì Í4 (ðòóòü) = 4,5 ì

Í2 (äåãîòü) = 10 ì Í5 (èçâåñòêîâîå òåñòî) = 7 ì

Í3 (ñêèïèäàð) = 5 ì Í6 (ìàçóò) = 10 ì

Ò.ê. àòìîñôåðíîå äàâëåíèå äåéñòâóåò îäèíàêîâî âî âñåõ òî÷êàõ, òî èñõîäÿ èç îñíîâíîãî óðàâíåíèÿ ãèäðîñòàòèêè Ð= Ðàò + ñgH äëÿ êàæäîé òî÷êè ãèäðîñòàòè÷åñêîå (èçáûòî÷íîå) äàâëåíèå âî âñåõ îòìå÷åííûõ òî÷êàõ Ðèçá= ñgH.

Òî÷êè:

Ð1=0

Ð2=ñ3gH3=8719,815=42722,6 Ïà=42,7 êÏà

Ð3=Ð2+ñ2gH2=42722,6+11009,8110=150,6 êÏà

Ð4=Ð2 +Ð3 +ñ1gH1=150,6+133409,813=543,2 êÏà

Ð5=0

Ð6=ñ6g3,5=9009,813,5=30901,5 Ïà=30,9 êÏà

Ð7=ñ6g8,5 – ñ3g5=9009,818,5 -8719,815=32,3 êÏà

Ð8=ñ6g10 – ñ3g5- ñ2g1,5=9009,8110 -8719,815 – 11009,811,5=29,4 êÏà

Ð9= ñ6g10 + ñ5g7 – Ð2 – ñ2g8,5=9009,8110 + 13609,817 – 42,71-10009,818,5=47,3 êÏà

Ð10= ñ6g10 + ñ5g7 + ñ4g1,5 – ñ3g5 – ñ2g10=9009,8110+13609,817+133409,811,5 -8719,815 -11009,8110=227,3 êÏà

Ð11= ñ6g10 + ñ5g7 + ñ4g4,5 – ñ3g5 – ñ2g10 – ñ1g3=9009,8110+13609,817+133409,814,5 -8719,815 – 11009,8110 – 133409,813=227,3 êÏà

Ð12=0

Ð13= ñ6g10=9009,8110=88,3 êÏà

Ð14= Ð13 + ñ5g7=88,3 + 13609,817=181,7 êÏà

Ð15= Ð14 + ñ4g4,5=181,7+133409,814,5=770,6 êÏà

Ïðîâåðêà: Ð15- Ð4 = Ð11;

770,6 – 543,2=227,3;

227,4?227,3 (íåâÿçêà 0,04%)

Ïîñòðîåíèå ýïþðû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ íà äíî è ñòåíêè ñîñóäîâ.

Ñïèñîê ó÷åáíîé ëèòåðàòóðû

1. Ïðîçîðîâ È.Â., Íèêîëàäçå Ã.È., Ìèíàåâ À.Â. «Ãèäðàâëèêà, âîäîñíàáæåíèå è êàíàëèçàöèÿ» -Ì. Âûñøàÿ øêîëà, 1990. -448ñòð.

2. Êàëèöóí Â.È., Êåäðîâ Â.Ñ., Ëàñêîâ Þ.Ì., Ñàôîíîâ Ï.Â. «Ãèäðàâëèêà, âîäîñíàáæåíèå è êàíàëèçàöèÿ»- Ì. Ñòðîéèçäàò, 2001.-298ñ.

3. Àëüòøóëü À.Ä., Êèñåëåâ Ï.Ã. «Ãèäðàâëèêà è àýðîäèíàìèêà».-Ì:Ñòðîéèçäàò,1975-212ñ.

4. Ýïîâ Ã.Ê., Êèì Ë.Á. «Ïðàêòèêóì ïî èíæåíåðíûì ñåòÿì».-Êàðàãàíäà:ÊàðÃÒÓ,2005.

5. Ëîÿöêèé Ë.Ã. «Ìåõàíèêà æèäêîñòè è ãàçà»-Ì:Íàóêà,1987-904ñ.

6. Äåé÷ Ì.Å., Çûðÿíêèí À.Å. «Ãèäðîäèíàìèêà».-Ì: Ýíåðãîèçäàò,1989-384ñ.

7. Êàëèöóí Â.È., Êåäðîâ Â.Ñ. è äð. «Îñíîâû ãèäðàâëèêè, âîäîñíàáæåíèÿ è êàíàëèçàöèè». -Ì: Ñòðîèçäàò,1980-359ñ. ñ èëë.

Ðàçìåùåíî íà Allbest.ru

…

Ïîäîáíûå äîêóìåíòû

Îïðåäåëåíèå êîýôôèöèåíòà óñòîé÷èâîñòè âîäîóäåðæèâàþùåé ñòåíêè îòíîñèòåëüíî ðåáðà “Î” ïðè çàäàííûõ ïåðåìåííûõ. Âû÷èñëåíèå äàâëåíèÿ ñèëû íà ó÷àñòêè ñòåíêè. Íàõîæäåíèå òî÷åê ïðèëîæåíèÿ ñèë, ïëîùàäè ýïþð è ñèëû äàâëåíèÿ. Îïðåäåëåíèå îïðîêèäûâàþùèõ ìîìåíòîâ.
êîíòðîëüíàÿ ðàáîòà [337,1 K], äîáàâëåí 13.10.2014
Îáçîð êðèòåðèåâ ïëàñòè÷íîñòè. Èçó÷åíèå ïðèìåðîâ îïðåäåëåíèÿ ýêâèâàëåíòíûõ íàïðÿæåíèé è êîýôôèöèåíòîâ çàïàñà. Ãèïîòåçà íàèáîëüøèõ êàñàòåëüíûõ íàïðÿæåíèé è ýíåðãèè ôîðìîèçìåíåíèÿ. Òîíêîñòåííûå îáîëî÷êè, íàõîäÿùèåñÿ ïîä äåéñòâèåì ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
êîíòðîëüíàÿ ðàáîòà [1,2 M], äîáàâëåí 11.10.2013
Ïîíÿòèå äàâëåíèÿ êàê ôèçè÷åñêîé âåëè÷èíû. Òèïû, îñîáåííîñòè óñòðîéñòâà äàò÷èêîâ äàâëåíèÿ: óïðóãèå, ýëåêòðè÷åñêèå ïðåîáðàçîâàòåëè, äàò÷èêè äèôôåðåíöèàëüíîãî äàâëåíèÿ, äàò÷èêè äàâëåíèÿ âàêóóìà. Äàò÷èêè äàâëåíèÿ, îñíîâàííûå íà ïðèíöèïå ìàãíåòîñîïðîòèâëåíèÿ.
ðåôåðàò [911,5 K], äîáàâëåí 04.10.2015
Íàõîæäåíèå äàâëåíèé â “õàðàêòåðíûõ” òî÷êàõ è ïîñòðîåíèå ýïþðû äàâëåíèÿ æèäêîñòè íà ñòåíêó â âûáðàííîì ìàñøòàáå. Îïðåäåëåíèå ñèëû äàâëåíèÿ æèäêîñòè íà ïëîñêóþ ñòåíêó è ãëóáèíû åå ïðèëîæåíèÿ. Ðàñ÷åò íåîáõîäèìîãî êîëè÷åñòâà áîëòîâ äëÿ êðåïëåíèÿ êðûøêè ëàçà.
êóðñîâàÿ ðàáîòà [641,4 K], äîáàâëåí 17.04.2016
Ïàêåò Flow Simulation ïðîãðàììû Solidworks 2012. Ìîäåëèðîâàíèå àýðîäèíàìè÷åñêîé òðóáû íà ïðèìåðå ÏÂÄ, ïîëó÷åíèå ýïþð ðàñïðåäåëåíèÿ äàâëåíèÿ. Ðàñïðåäåëåíèå äàâëåíèÿ âáëèçè êîðïóñà. Äèíàìè÷åñêîå äàâëåíèå âíóòðè òðóáêè Ïèòî. Ïðèåìíèê ñòàòè÷åñêîãî äàâëåíèÿ.
êóðñîâàÿ ðàáîòà [1,3 M], äîáàâëåí 29.05.2014
Íàçíà÷åíèå ãàáàðèòíûõ ðàçìåðîâ öèëèíäðè÷åñêîãî ðåçåðâóàðà íèçêîãî äàâëåíèÿ. Êîíñòðóèðîâàíèå äíèùà è îïðåäåëåíèå òîëùèíû ëèñòîâ ñòåíêè. Ðàñ÷åò àíêåðíûõ êðåïëåíèé è êîíñòðóèðîâàíèå ýëåìåíòîâ ñôåðè÷åñêîãî ïîêðûòèÿ. Ïðîâåðêà ñòåíêè ðåçåðâóàðà íà óñòîé÷èâîñòü.
êóðñîâàÿ ðàáîòà [513,0 K], äîáàâëåí 16.07.2014
Åäèíèöû èçìåðåíèÿ äàâëåíèÿ, îñíîâíîå óðàâíåíèå ãèäðîñòàòèêè, ïàðàìåòðû ñæèìàåìîñòè æèäêîñòè, óðàâíåíèå Áåðíóëëè. Ðàñõîä æèäêîñòè ïðè èñòå÷åíèè ÷åðåç îòâåðñòèå èëè íàñàäêó, ðåæèìû äâèæåíèÿ æèäêîñòè. Ãèäðàâëè÷åñêèå öèëèíäðû, íàñîñû, ðàñïðåäåëèòåëè, áàêè.
òåñò [525,3 K], äîáàâëåí 20.11.2009
Ðåãóëèðîâàíèå è êîíòðîëü äàâëåíèÿ ïàðà â ïàðîâîé ìàãèñòðàëè äëÿ êà÷åñòâåííîé ðàáîòû êîíâåéåðà òâåðäåíèÿ. Ñòàáèëèçàöèÿ äàâëåíèÿ ñ ïîìîùüþ ïåðâè÷íîãî ïðåîáðàçîâàòåëÿ äàò÷èêà äàâëåíèÿ Ìåòðàí-100Äè. Âûáîð ðåãóëèðóþùåãî óñòðîéñòâà, ñðåäñòâ àâòîìàòèçàöèè.
êóðñîâàÿ ðàáîòà [318,8 K], äîáàâëåí 09.11.2010
Æèäêîñòü è åå îñíîâíûå ôèçè÷åñêèå ñâîéñòâà, îïðåäåëåíèå è îñíîâíûå ñâîéñòâà æèäêîñòè. Ãèäðîñòàòèêà è ãèäðîñòàòè÷åñêîå äàâëåíèå, îñíîâíîå óðàâíåíèå ãèäðîñòàòèêè. Ïîíÿòèå î ïüåçîìåòðè÷åñêîé âûñîòå è âàêóóìå, ñèëà äàâëåíèÿ æèäêîñòè íà ïîâåðõíîñòè.
êóðñîâàÿ ðàáîòà [2,1 M], äîáàâëåí 17.11.2009
Îáùåå îïèñàíèå ïðèáîðîâ. Èçìåðåíèå äàâëåíèÿ. Êëàññèôèêàöèÿ ïðèáîðîâ äàâëåíèÿ. Îñîáåííîñòè ýêñïëóàòàöèè Èíäèâèäóàëüíîå çàäàíèå. Ïðåîáðàçîâàòåëü äàâëåíèÿ Ñàïôèð-22-Åx-Ì-ÄÄ. Íàçíà÷åíèå. Óñòðîéñòâî è ïðèíöèï ðàáîòû ïðåîáðàçîâàòåëÿ. Íàñòðîéêà ïðèáîðà.
ïðàêòè÷åñêàÿ ðàáîòà [25,4 K], äîáàâëåí 05.10.2008

Эпюра давления на дно сосуда