К дну высокого цилиндрического сосуда
Тема. Решение задач по теме “Гидростатика и гидродинамика”.
Цели:
- – рассмотреть основные приемы решения расчетных задач на тему “Гидростатика и гидродинамика”.
Ход занятия
В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач.
Прежде чем приступить к выполнению задания, следует повторить основные законы гидромеханики.
Основной закон гидростатики – закон Паскаля, согласно которому в состоянии равновесия давление жидкости в данной точке не зависит от ориентации площадки, на которую она действует.
Поскольку в школьном курсе рассматривается стационарное течение несжимаемой жидкости, то будет справедливо уравнение неразрывности струи.
Для идеальной жидкости выполняется уравнение Бернулли. Покажите, что уравнение Бернулли является следствием закона сохранения энергии.
Качественные задачи
- К концам равноплечного рычага подвесили две одинаковые гири. Что произойдет, если одну гирю поместить в воду, а другую в керосин?
Ответ: равновесие нарушится.
- Почему, если близко стоишь около быстро идущего поезда, возникает эффект “притягивания” к колесам?
Ответ: проходящий поезд увлекает за собой примыкающие к нему слои воздуха. Воздух, движущийся между человеком и поездом, оказывает на него меньшее давление, чем неподвижный. Эта разность давлений и обусловливает силу, увлекающую человека к поезду.
- При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял свой самолет. Как можно объяснить это явление?
- Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Ответ: чем сильнее вы вдуваете воздух, тем плотнее фильтр входит в воронку. Объясняется это с помощью закона Бернулли, согласно которому давление понижается в местах сужения. В узком просвете между воронкой и бумажным фильтром давление понижается, и внешнее атмосферное давление удерживает фильтр в воронке.
Примеры решения расчетных задач
Задача 1. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S1, сечение струи S2 (рис. 2). Найдите ускорение, с которым перемещается уровень воды в сосуде.
Решение:
Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать
S1v1 = S2v2, (1)
где v1 – скорость воды в сосуде, v2 – скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1)
,
где – ускорение воды в сосуде, – ускорение свободного падения, так на выходе из сосуда вода начинает свободно падать. Таким образом,
.
Ответ: .
Задача 2. В сосуде с жидкостью сделано отверстие площадью S. Размеры отверстия малы по сравнению с высотой столба жидкости. В одном случае отверстие закрыто пластинкой и измеряется сила давления жидкости на пластинку F1 при высоте столба жидкости h (рис. 3). В другом случае тот же сосуд стоит на тележке, отверстие открыто, и измеряется сила отдачи F2 при установившемся токе жидкости в момент, когда высота столба жидкости будет та же, что и в первом случае. Будут ли силы F1 и F2 равны?
Решение:
Согласно закону Паскаля давление на жидкость передается во всех направлениях одинаково, поэтому в первом случае давление, производимое на пластинку жидкостью, равно гидростатическому давлению столба жидкости высотой h, а значит, F1 = ρghS , где ρ – плотность жидкости.
Во втором случае сила F2 согласно второму закону Ньютона равна изменению импульса жидкости в единицу времени
.
Изменение импульса Δp = Δmv , где Δm – масса жидкости, вытекающей в единицу времени, v – скорость истечения жидкости из отверстия.
Масса вытекающей жидкости Δm = ρgS, скорость истечения согласно формуле Торричелли . Следовательно,
F2 = ρv2S = 2ρghS.
Таким образом, F2 = 2F1 . Объяснить это можно так. Когда жидкость вытекает из малого отверстия, линии тока вблизи него сгущаются, а значит, как следует из уравнения Бернулли, давление на стенку вблизи отверстия уменьшается. Поэтому сила реакции вытекающей струи оказывается больше силы статического давления на площадь отверстия.
Ответ: силы F1 и F2 не равны.
Задача 3. Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b (рис. 3). Сколько воды вытечет из крана за время t?
Решение:
Воспользуемся условием стационарности течения несжимаемой жидкости
. (1)
Для идеальной жидкости справедливо уравнение Бернулли:
.
Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:
. (2)
За время t через любое сечение протекает один и тот же объем воды, поэтому можно записать
. (3)
Выразим скорость v1 из (1) и (2):
.
Подставим полученное значение v1 в (3) и получим окончательный ответ:
.
Ответ: .
Задача 4. Площадь поршня в шприце S1 = 2 см2, а площадь отверстия S2 = 1 мм2 (рис. 4). Сколько времени будет вытекать вода из шприца, если действовать на поршень с силой F = 5 H и если ход поршня l = 5 см?
Решение:
Так как из шприца вытечет вся находившаяся в нем жидкость, то
S1l = S2v2t, (5)
где v2 – скорость истечения струи. Будем считать жидкость идеальной, тогда можно использовать уравнение Бернулли:
.
Шприц расположен горизонтально, следовательно, h = const. Уравнение Бернулли тогда запишется следующим образом:
, (6)
где Ра – атмосферное давление, а v1 – скорость движения поршня. Из уравнения неразрывности следует
S1v1 = S2v2. (7)
Решая совместно уравнения (6) и (7), получим
,
отсюда
.
Подставляя найденное значение v2 в (5), получим
.
Так как S2S1 , то можно записать
.
Ответ:
Задачи для самостоятельной работы
- “Вечерело. Уставший за нелегкий трудовой день Абдулла Ибн Сауд присел на берегу реки и стал обдумывать свой социальный статус. В колхоз не берут, кооперативы эмир разогнал, к нему самому на службу устраиваться – так стражники без золотых во дворец не пускают. Эх, жизнь… Но тут взгляд Абдуллы остановился: по реке плыл какой-то предмет, и лишь маленький кусочек сургуча был виден над водой. Абдулла бросился в воду и вытащил оттуда старинный глиняный кувшин, герметично закупоренный сургучом. Распечатав кувшин и перевернув его, Абдулла обомлел: сверкнуло золото. Из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а сосуд запечатал и бросил обратно в воду. Поплыл сосуд дальше, примерно треть его объема торчало над водой”.
Так говорится в одной из восточных сказок. Предполагая, что кувшин был двухлитровый, оцените массу одной золотой монеты.Ответ: m = 4,45 г.
- На некоторых железных дорогах пополнение паровозного котла водой производится без остановки паровоза. Для этой цели применяется изогнутая под прямым углом труба, которая опускается на ходу паровоза в канаву с водой, проложенную вдоль рельсов. При какой скорости паровоза вода может подняться на высоту 3 м?
Ответ: v = 28 км/ч.
- Из поднятого на высоту h резервуара выходит труба постоянного сечения S, переходящая в короткую трубу сечением S1, перекрытую краном. Найдите давление в магистральной трубе при открытом кране.
Ответ: Р = Ратм + ρgh.
- Определите расход воды Q, протекающей через слив плотины, имеющей ширину l, глубину потока d и понижение уровня потока по сравнению с уровнем воды в водохранилище, равное h.
Ответ: Q = ρdl·√(2gh).
- Какова примерно скорость катера, если при его движении вода поднимается вдоль его носовой части
на высоту h = 1 м?Ответ: v ≈ √(2gh) ≈ 4,4 м/с.
- На гладкой горизонтальной поверхности стоит цилиндрический сосуд с водой. В боковой стене сосуда у дна имеется отверстие площадью S0. Какую силу нужно приложить к сосуду в горизонтальном направлении, чтобы удержать его в равновесии? Площадь поперечного сечения сосуда равна S, высота столба жидкости h.
Ответ: .
- На поршень шприца площади S действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади s? Плотность жидкости ρ. Трением пренебречь.
Ответ: . Если s S, то .
Рекомендуемая литература
- Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 332-352.
- Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 420-436.
- Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 63-67.
- Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр “Март”, 2004. – С. 184-212.
Источник
.
Поскольку
труба горизонтальна, то
.
Уровни жидкости в манометрических
трубках характеризует давление жидкости
в сечении:
и
,
где
– давление на оси трубки,
и
– уровень жидкости в манометрических
трубках. Тогда,
,
,
.
Согласно теореме
о непрерывности
.
Решая совместно
последние два уравнения, получим
,
,
.
Объём
жидкости, протекающий в единицу времен
через сечение трубы, равен
.
8.2.
Вертикальная
струя идеальной жидкости вытекает из
горизонтального отверстия радиуса r
со скоростью
.
Найти радиус струи r
на уровне h
ниже отверстия.
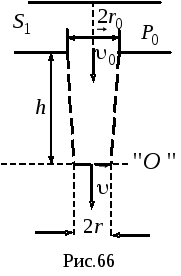Решение.
Из уравнения
непрерывности (рис.66):
,
.
Запишем уравнение
Бернулли:
.
Давление
в любой точке равно P
-атмосферному
давлению. Высота h
отсчитывается от уровня
,
положение которого показано на рис.66.
После математических преобразований
получим
,
тогда
.
8.3.
Из отверстия
в дне высокого цилиндрического сосуда
вытекает вода. Площадь сечения сосуда
в
раз больше сечения отверстия. Найти
ускорение, с которым перемещается
уровень воды в сосуде.
Решение.
Рассмотрим
два уровня жидкости (рис.67), один – на
уровне свободной поверхности жидкости
в цилиндре (координата x),
другой – на уровне отверстия снаружи.
Вблизи отверстия и на уровне x
давление атмосферное P0.
,
.
Согласно уравнению
непрерывности
,
откуда
,
.
Продифференцируем
последнее уравнение по времени:
.
Знак
«–» в правой части появляется вследствие
того, что
(уровень понижается).
или в векторной
форме:
.
Завершим
этот раздел рассмотрением течения
вязкой жидкости. В этом случае между
слоями жидкости действует сила трения,
рваная
,
где
– коэффициент внутреннего трения или
вязкость, S
– площадь соприкосновения слоёв жидкости,
– градиент модуля скорости в направлении,
перпендикулярном S.
8.4*.
По трубе радиуса R
течёт стационарный поток вязкой жидкости.
На оси трубы её скорость
.
Найти скорость жидкости как функцию
расстояния r
от оси трубы.
Решение.
Скорость
жидкости у стенок трубы равна нулю, а
на оси
.
Выделим цилиндрический объём жидкости
радиуса r
и длины l
(рис.68). Поскольку все элементы жидкости
движутся без ускорения, то сумма всех
сил, действующих на этот объём равна
нулю. В проекции на ось X:
,
где
P1
и P2
– давления
жидкости на переднее и заднее основания
выделенного цилиндрического объема
соответственно.
Сила
трения, действующая между двумя слоями
жидкости, равна:
,
где
S
– площадь поверхности выделенного
объёма. Кроме того
.
Поэтому,
,
.
Проинтегрируем
левую часть полученного выражения от
до 0 (скорость у стенок равна 0), а правую
от r
до R
.
.
При
r = 0
,
откуда
.
1. Кинематика
Задачи
этого параграфа носят иллюстративный
характер, то есть представляют собой
выводы, основанные на применении
преобразований Лоренца, некоторых
основных положений специальной теории
относительности (сокращение длин,
изменение промежутков времени,
относительность понятия одновременности
событий).
Решение задач
Лоренцево
сокращение длины
9.1.
Стержень движется в продольном направлении
с постоянной скоростью
относительно инерциальной K-системы
отсчёта. При каком значении
длина стержня в этой системе отсчёта
будет на
меньше его собственной длины?
Решение.
В системе
отсчёта, связанной с самим стержнем,
его длина l
– собственная длина, которая связана с
его длиной l
в системе K
соотношением:
.
По
условию задачи
:
,
откуда
.
9.2.
Найти собственную длину стержня, если
в некоторой K-системе
отсчёта его скорость
,
длина l
и угол между ним и направлением движения
.
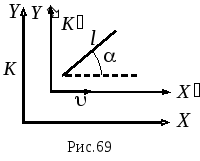Решение.
В поперечном
направлении (оси
и
рис.69) длина стержня не меняется, то есть
.
Вдоль
оси X
в системе K
длина стержня
,
в системе, связанной со стержнем, его
длина в этом направлении lx
и связь между ними:
,
,
тогда собственная
длина:
,
,
где
.
Замедление
хода движущихся часов
9.3.
Собственное время жизни некоторой
нестабильной частицы
.
Какой путь пролетит эта частица до
распада в лабораторной системе отсчёта,
где её время жизни
.
Решение.
Путь l,
пройденный частицей в лабораторной
системе отсчёта:
.
Связь между
и
:
,
где
.
Поэтому
,
.
9.4.
С какой скоростью двигались в K-системе
отсчёта часы, если за время t
(в K-системе)
они отстали от часов этой системы на
.
Решение.
Пусть в
момент t = 0
в системе K,
движущиеся часы показывали тоже t0 = 0.
Тогда:
и
.
2. Динамика
В
релятивистской механике импульс частицы
массы m, движущейся
со скоростью
.
Полная
энергия такой частицы
.
Решение задач
9.5.
Найти скорость, при которой релятивистский
импульс частицы в
раз (
)
превышает её Ньютоновский импульс.
Решение.
Релятивистский
импульс:
.
Ньютоновский
импульс
.
По условию задачи:
,
.
9.6.
При какой
скорости кинетическая энергия частицы
равна её энергии покоя?
Решение.
Кинетическая
энергия частицы определяется как:
,
то
есть как разность между полной энергией
и энергией покоя. По условию задачи
,
.
По
существу, в теории относительности при
любом характере взаимодействия тел
(при отсутствии внешних воздействий)
всегда справедливы законы сохранения
импульса и энергии. Полная энергия
частиц E
и их импульс Pсвязаны
соотношением
,
где
M
– масса образовавшейся частицы.
9.10.
Две частицы,
каждая массы m,
летят навстречу друг другу с одинаковой
скоростью
.
Найти
,
если масса образовавшейся при столкновении
частицы равна M.
Решение.
Полная
энергия частицы E
и ее импульс P
связаны
соотношением
,
где
M
– масса образовавшейся частицы. В нашем
случае P = 0,
так как две одинаковые частицы движутся
навстречу друг другу с одинаковыми
скоростями, следовательно, скорость
образовавшейся частицы равна нулю. До
столкновения полная энергия двух частиц:
.
Поэтому
,
откуда
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 1448
Из крана выливается вода. Начиная с некоторого места диаметр струи уменьшается на протяжении $h$ от $b$ до $c$.
Сколько воды вытечет из крана за время $t$?
Подробнее
Задача по физике – 1449
Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности $rho$. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха $P_{0}$.
Подробнее
Задача по физике – 1450
Сосуд с водой подвешен к потолку. Высота воды в сосуде $H$. На сколько изменится натяжение веревки, если в днище сосуда открыть маленькое отверстие сечения $S$, из которого вытекает вода?
Подробнее
Задача по физике – 1451
Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда $S_{1}$, сечение струи $S_{2}$. Уровень воды в сосуде перемещается с постоянным ускорением. Найдите это ускорение.
Подробнее
Задача по физике – 1452
Насос должен подавать ежесекундно объем воды $Q$ на высоту $H$ по трубе постоянного сечения $S$. Какова должна быть мощность насоса? КПД насоса $eta$, плотность воды $rho$.
Подробнее
Задача по физике – 1453
По трубе сечением $S$, изогнутой под прямым углом, течет вода со скоростью $v$. Плотность воды $rho$.
Чему равна сила бокового давления в месте закругления трубы?
Подробнее
Задача по физике – 1821
Как вы думаете, справедлив ли закон сообщающихся Сосудов (однородная жидкость в сообщающихся сосудах имеет один и тот же уровень), если в одном из сосудов на поверхности жидкости находится некоторый поплавок (капиллярность не учитывать)?
Подробнее
Задача по физике – 1822
Достаточно длинная открытая снизу трубка с плотно пригнанным поршнем, который может все же двигаться по трубке без трения, находится под водой и удерживается с помощью веревки (рис.). Верхний конец трубки над поршнем пустой. Как зависит сила натяжения веревки от глубины погружения трубки в воду?
Подробнее
Задача по физике – 1823
Ведро, имеющее массу $m$, вместимость $V$, вытаскивают с водой из колодца. Плотность материала, из которого сделано ведро, равна $rho$, плотность воды $rho_{в}$. Какую силу необходимо приложить для подъема этого ведра, пока оно находится под водой и когда его вытащили из воды? Сопротивление воды движению ведра не учитывать.
Подробнее
Задача по физике – 1824
Для того чтобы поднять уровень жидкости в сосуде на Высоту $h$ с помощью насоса, надо совершить некоторую работу. Изменится ли необходимая для этой же цели работа, если на поверхности жидкости плавает какое-нибудь тело?
Подробнее
Задача по физике – 1825
Изменится ли осадка парохода, перешедшего из северных вод в экваториальные, вследствие изменения ускорения свободного падения с широтой?
Подробнее
Задача по физике – 1826
Как зависит подъемная сила аэростата от температуры, при которой производится его подъем?
Подробнее
Задача по физике – 1827
Когда объясняют опыт со взвешиванием воздуха, [иногда говорят, что сначала взвешивают колбу с воздухом, а затем, после откачки воздуха из колбы, взвешивают одну колбу. Разность показаний весов в первом и втором случаях и составляет массу воздуха в объеме колбы. Правильно ли такое толкование опыта по взвешиванию воздуха?
Подробнее
Задача по физике – 1828
Можно ли измерить плотность воздуха, взвешивая мягкий воздухонепроницаемый мешок сначала пустой (сжатый), а потом наполненный воздухом? Объем мешка в наполненном Состоянии известен.
Подробнее
Источник