Как движется молекула газа в сосуде

§9. Молекулярно-кинетическая теория идеального газа

9.1. Модель идеального газа в молекулярно-кинетической теории

Законы идеальных газов, найденные опытным путём, находят довольно простое объяснение в молекулярно-кинетической теории (МКТ). Она исходит при этом из упрощённых представлений о строении газа. Это обусловлено рядом причин, в частности, неточным знанием сил взаимодействия между молекулами. Однако, как оказывается, даже такая упрощённая модель газа позволяет найти уравнение состояния, правильно описывающее его поведение.

В молекулярно-кинетической теории принимается следующая идеализированная модель газа – идеальный газ. Молекулы газа считаются твёрдыми, абсолютно упругими шариками, причём размеры молекул малы по сравнению со средним расстоянием между ними. Это означает, что собственный суммарный объём молекул значительно меньше объёма сосуда, в котором находится газ. Взаимодействие между молекулами проявляется только при непосредственном столкновении их друг с другом. Между столкновениями молекулы движутся по инерции. Движение молекул подчиняется законам механики Ньютона.

Для нахождения уравнения состояния газа необходимо сделать ещё важное упрощающее предположение, а именно, считать движение любой молекулы газа беспорядочным, хаотичным.

Аккуратный вывод основного уравнения молекулярно-кинетической теории идеального газа требует принимать во внимание ряд моментов, например, наличие в газе молекул, движущихся с разными по величине скоростями, столкновения молекул между собой, характер столкновения отдельной молекулы со стенкой сосуда (упругий или неупругий). В разделе 7.3 будет рассмотрен упрощённый вариант вывода основного уравнения молекулярно-кинетической теории.

9.2. Давление идеального газа

Давление, которое оказывает газ на стенку сосуда, есть результат ударов молекул газа о стенку. Если бы в сосуде содержалось всего несколько молекул, то их удары следовали бы друг за другом редко и беспорядочно. Поэтому нельзя было бы говорить ни о какой регулярной силе давления, действующей на стенку. Стенка подвергалась бы отдельным практически мгновенным бесконечно малым толчкам. Если же число молекул в сосуде очень велико, то велико и число ударов их о стенку сосуда. Одновременно о стенку сосуда ударяется громадное количество молекул. Очень слабые силы отдельных ударов складываются при этом в значительную по величине и почти постоянную силу, действующую на стенку. Среднее по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа, с которым имеет дело термодинамика.

Пусть в сосуде объёма $$ V$$ находятся $$ N$$ одинаковых молекул идеального газа, а $$ {m}_{0}$$ – масса одной молекулы. В рамках молекулярно-кинетической теории показывается, что давление $$ p$$ газа определяется выражением:

p = m 0 n v 2 ¯ / 3 p = m_0nbar{v^2}/3 , (11)

где $$ n=N/V$$ – концентрация молекул газа, v 2 ¯ bar{v^2} – среднее значение квадрата скорости молекулы. Выражение (11) называют основным уравнением молекулярно-кинетической теории идеального газа.

Заметим, что величина m 0 v 2 ¯ / 2 m_0bar{v^2}/2 есть средняя кинетическая энергия E ¯ bar{E} поступательного движения молекулы. Поэтому полученную формулу можно представить в другом виде:

p = 2 n E ¯ / 3 p = 2nbar E / 3 . (12)

Ниже приводится один из способов вывода уравнения (11). Данный раздел при первом прочтении можно пропустить.

9.3* Вывод основного уравнения МКТ идеального газа

Вычислим среднее давление газа на стенку сосуда.

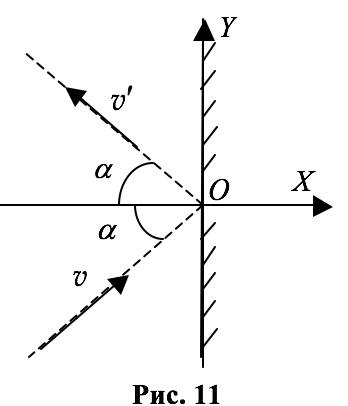
Для простоты будем считать, что удар молекулы о стенку происходит абсолютно упруго, а сама стенка идеально гладкая и молекула после удара отражается от неё под тем же углом, под каким она падала на стенку (см. рис. 11), или, как говорят, зеркально (однако ясно, что никаких гладких стенок не существует: ведь сама стенка состоит из молекул).

Введём систему координат, направив ось $$ OX$$ перпендикулярно стенке, а ось $$ OY$$ – вдоль стенки (см. рис. 11).

Пронумеруем все молекулы от $$ i=1$$ до $$ i=N$$. Пусть $$ {v}_{i,x},({v}_{i,x}>0) -$$ проекция скорости $$ i$$-ой молекулы на ось $$ OX$$ до удара. При абсолютно упругом ударе о стенку проекция скорости на ось $$ OX$$ изменяет знак: $$ {v}_{i,x}^{text{‘}}=-{v}_{i,x}$$. Изменение проекции импульса молекулы на ось $$ OX$$ при столкновении молекулы со стенкой равно:

$$ mathrm{Delta }{p}_{i,x}={m}_{0}{v}_{i,x}^{text{‘}}-{m}_{0}{v}_{i,x}=-2{m}_{0}{v}_{i,x}$$,

а передаваемый стенке импульс равен:

$$ mathrm{Delta }{p}_{i,x,mathrm{стен}}=-mathrm{Delta }{p}_{i,x}=2{m}_{0}{v}_{i,x}$$.

Так как давление газа не зависит от формы сосуда, возьмём для простоты сосуд в форме куба с ребром $$ l$$. Тогда промежуток времени между двумя последовательными столкновениями молекулы с одной и той же стенкой составит $$ {tau }_{i}=2l/{v}_{i,x}$$, а за большой интервал времени $$ t$$ она столкнётся со стенкой $$ {N}_{mathrm{столк},i}=t/{tau }_{i}$$ раз. Переданный стенке одной молекулой за это время импульс равен:

`2m_0v_(i,x)*N_(“столк”,i)=2m_0v_(i,x)*(v_(i,x)t)/(2l)=m_0v_(i,x)^2*t/l`.

Так как в сосуде находятся $$ N$$ молекул, то полный переданный стенке импульс всех молекул равен:

$$ mathrm{Delta }{p}_{x,sum }=sum _{i=1}^{i=N}Delta {p}_{i,x,mathrm{стен}}={displaystyle frac{{m}_{0}t}{l}}sum _{i=1}^{i=N}{v}_{i,x}^{2}$$.

Среднюю силу давления на стенку можно получить, разделив полный передаваемый стенке импульс на время $$ t$$:

`F_(x,”ср”)=(Deltap_(x,sum))/t=m_0/l sum_(i=1)^(i=N) v_(i,x)^2`,

а давление $$ p -$$ разделив эту силу на площадь стенки $$ S={l}^{2}$$:

`p=(F_(x,”ср”))/S=m_0/l^3 sum_(i=1)^(i=N) v_(i,x)^2=m_0/V sum_(i=1)^(i=N) v_(i,x)^2`.

Здесь учтено, что объём сосуда $$ V={l}^{3}$$. Если ввести среднее значение квадрата проекции скорости одной молекулы:

`bar(v_x^2)=1/N sum_(i=1)^(i=N) v_(i,x)^2`,

то для давления $$ p$$ получаем:

$$ p={displaystyle frac{{m}_{0}N}{V}}overline{{v}_{x}^{2}}$$.

Входящую в это выражение величину $$ overline{{v}_{x}^{2}}$$ можно выразить через среднее значение квадрата скорости молекулы. Из соотношения $$ {v}^{2}={v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}$$ для средних значений имеем: $$ overline{{v}^{2}}=overline{{v}_{x}^{2}}+overline{{v}_{y}^{2}}+overline{{v}_{z}^{2}}$$. Так как движение молекул беспорядочное, то все направления движения равновероятны и средние значения квадратов проекций на любое направление должны быть равны $$ overline{{v}_{x}^{2}}=overline{{v}_{y}^{2}}=overline{{v}_{z}^{2}}$$. Отсюда получаем: $$ overline{{v}^{2}}=3overline{{v}_{x}^{2}}$$, что позволяет записать выражение для давления в виде:

$$ p={displaystyle frac{1}{3}}{displaystyle frac{{m}_{0}N}{V}}overline{{v}^{2}}, mathrm{или} p={displaystyle frac{1}{3}}{m}_{0}noverline{{v}^{2}}$$,

где $$ n=N/V$$ концентрация молекул газа.

Источник

Это уравнение устанавливает связь между давлением и средней энергией теплового движения молекул. Давление, оказываемое газом на стенки сосуда, является результатом передачи стенке импульса сталкивающихся с ней молекул. При расчетах учтем, что движение молекул хаотично, и удары молекул об стенку являются абсолютно-упругими. Рассмотрим одноатомный газ, занимающий объем (рис. 1). Выделим на стенке сосуда элементарную поверхность и вычислим давление, оказываемое на эту поверхность. При соударении со стенкой молекула с

Рис.1

массой , движущаяся со скоростью перпендикулярно стенке, передает ей импульс . За время поверхности стенки достигнут только те молекулы которые заключены в объеме цилиндра с основанием и высотой .Это число молекул равно , где – число молекул в единице объема. Здесь мы упростили рассмотрение движения молекул. На самом деле молекулы к площадке движутся под разными углами, имея различные скорости. Для упрощения расчета хаотическое движение молекул по всем направлениям обычно заменяют движением вдоль трех взаимно перпендикулярных координатных осей так, что в любой момент времени вдоль каждой из них (например, оси х) движется 1/3 общего числа молекул, причем одна половина из этого числа, т.е. 1/6 часть молекул, движется вдоль положительной оси, другая половина – в противоположном направлении. Тогда число ударов о поверхность за время будет равно /6 При столкновении с поверхностью молекулы передают ей импульс . Воспользовавшись вторым законом Ньютона , можем выразить силу давления на поверхность

.

Давление газа на стенку выразится в виде

. (2.8)

Молекулы в сосуде движутся с самыми различными скоростями . Их общее число . Поэтому вместо скорости в эту формулу следует подставлять среднюю квадратичную скорость, которая характеризует всю совокупность молекул

. (2.9)

Поэтому

(2.10)

Здесь – средняя кинетическая энергия поступательного движения молекул. Тогда уравнение (2.10) перепишется в виде

. (2.11)

Таким образом, давление газа пропорционально средней кинетической энергии теплового движения молекул газа, заключенных в единице объема. Полученное выражение носит название основного уравнения молекулярно-кинетической теории газов.

Следствия из основного уравнения молекулярно-кинетической теории газов

Так как , то получаем

, (2.12)

где – средняя энергия поступательного движения всех молекул газа.

Отсюда (2.13)

С помощью уравнения Клапейрона-Менделеева

легко получаем

,

откуда

. (2.14)

Энергия поступательного движения одного моля газа будет равна

.

Поделив это уравнение на число Авогадро , получаем

.

Формула

(2.15)

имеет глубокий физический смысл – она выражает, что термодинамическая температура зависит толь от средней энергии поступательного движения молекул.

Существенно также, что средняя кинетическая энергия молекул зависит только от температуры и не зависит от массы молекул. При абсолютно нулевой температуре Т = 0 поступательное движение молекул прекращается. Подставив

в (2.15), получаем выражение для среднеквадратичной скорости в виде

(2.16)

Умножая числитель и знаменатель дроби под корнем на число Авогадро, получим

(2.17)

Источник

В жизни мы встречаем газообразное состояние вещества, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (он занимает весь предоставленный ему объем), состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Агрегатных состояния точно три?

На самом деле, есть еще четвертое – плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ – газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Давление газа

Мы только что выяснили, что молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.

Например, в комнате, в которой вы сейчас находитесь, на каждый квадратный сантиметр за 1 с молекулами воздуха наносится столько ударов, что их количество выражается двадцати трехзначным числом.

Хотя сила удара отдельной молекулы мала, действие всех молекул о стенки сосуда приводит к значительному давлению. Это как если бы один комар толкал машину, то она бы и не сдвинулась с места, а вот пару сотен миллионов комаров вполне себе способны эту машину сдвинуть.

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает: давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление

p = F/S

p – давление [Па]

F – сила [Н]

S – площадь [м^2]

То есть, если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы они толкали грузовой автомобиль (просто потому что легковая меньше грузовика).

Из формулы давления следует, что давление на легковой автомобиль будет больше из-за меньшей площади.

Давайте рассмотрим аналогичный пример с двумя сосудами разной площади.

Давление в левом сосуде будет больше, чем во втором, по аналогичной схеме – потому что площадь меньше. Но если площадь основания меньше, то и объем меньше. Это значит, что давление будет зависеть от объема следующим образом: чем больше объем, тем меньше давление – и наоборот.

При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

Такая зависимость называется законом Бойля-Мариотта.

Она экспериментально проверяется с помощью такой установки.

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в Жаком Шарлем.

Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке.

Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру, а соответствующее давление – по манометру.

Этот эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейно:

Эта зависимость называется законом Шарля.

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое, или когда газы необходимо длительно хранить – их помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или любым способом пытаться сделать в них отверстие, даже после использования.

Понимать и любить этот мир проще, когда разбираешься в физике. В этом помогут небезразличные и компетентные преподаватели онлайн-школы Skysmart.

Чтобы формулы и задачки ожили и стали более дружелюбными, на уроках мы разбираем примеры из обычной жизни современных подростков. Приходите на бесплатный вводный урок по физике и начните учиться в удовольствие уже завтра!

Источник