Как изменится h если в u образный сосуд залить ртуть
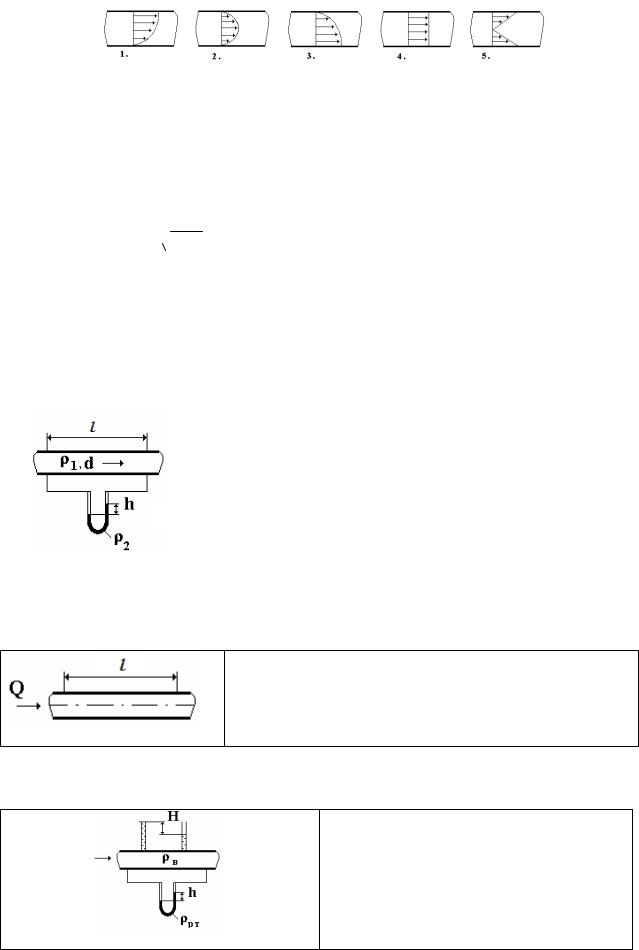
В U-образный сосуд налиты ртуть и вода. Линия раздела жидкостей расположена ниже свободной поверхности ртути на hpт=2 см. Определить разность уровней h в обеих частях сосуда.
Дано:
ρводы=1000 кг/м3;
ρртути=13600 кг/м3;
hрт=2 см =0,02 м.
Определить:
H
Решение:
Запишем уравнение для определения абсолютного гидростатического давления на уровне раздела жидкостей в левом колене U-образного сосуда:
(1)
где ра – атмосферное давление на свободной поверхности воды в левом колене U-образного сосуда, Па;
ρвghв – вес столба воды высотой hв, Па.
В правом колене на этом уровне абсолютное гидростатическое давление определяется по следующему выражению:
(2)
где ра атмосферное давление на свободной поверхности ртути в правом колене U-образного сосуда, Па;
ρpтghpт – вес столба ртути высотой hpт, Па.
Так как абсолютное гидростатическое давление на выбранном уровне в правом и левом колене U-образного сосуда будет одинаковым, то уравнения (1) и (2) можно приравнять:
Вариант №1
1) Уровень мазута в вертикальном цилиндрическом баке диаметром 2 м за некоторое время понизился на 0,5 м. Определить массу израсходованного мазута, если плотность его при температуре окружающей среды 20 °С равна ρ=990 кг/м3.
2) Найти давление на свободной поверхности в закрытом сосуде с бензином, если уровень жидкости в открытом пьезометре выше уровня жидкости в сосуде на h=2 м, а атмосферное давление ра=100 кПа.
3) Определить величину силы гидростатического давления воды на вертикальный щит шириной b=2 м, если глубина воды перед щитом Н=2,7 м.
4) Определить давление p1 в сечении 1-1 горизонтально расположенного сопла, необходимое для придания скорости воде в выходном сечении 2-2 V2=40 м/с (р2= ра), если скорость движения воды в сечении 1-1 V1=3 м/с.
5) Построить график зависимости коэффициента гидравлического трения λ от числа Рейнольдса в водопроводной трубе D=150 мм при расходе, изменяющемся в пределах Q=1÷30 л/с, кинематическом коэффициенте вязкости υ = 0,013 см2/с, если трубы асбестоцементные.
6) Из бака при постоянном напоре Н по трубопроводу, имеющем уклон, характеризуемый следующими данными: отметка сечения 1-1 z1=5 м, сечения 4-4 z4=3 м, длиной I=100 м и диаметром D=0,1 м вытекает вода в атмосферу. На расстоянии I1=80 м от начала трубопровода установлен вентиль. Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии, если Н=5 м; λ=0,03.
Вариант №2
1) Уровень мазута в вертикальном цилиндрическом баке диаметром 1,8 м за некоторое время понизился на 1 м. Определить массу израсходованного мазута, если плотность его при температуре окружающей среды 20°С равна ρ=990 кг/м3.
2) В U-образный сосуд налиты ртуть и вода. Линия раздела жидкостей расположена ниже свободной поверхности ртути на hpт=8 см. Определить разность уровней h в обеих частях сосуда.
3) Определить силу давления воды на дно сосуда и на каждую из четырех опор. Собственным весом сосуда пренебречь.
4)Определить давление p1 в сечении 1-1 трубопровода, необходимое для придания скорости воде в сечении 2-2 V2=20 м/с (р2=90 кПа) если скорость движения воды в сечении 1-1 V1=5 м/с.
5)Построить график зависимости коэффициента гидравлического трения λ от числа Рейнольдса в водопроводной трубе D=150 мм при расходе, изменяющемся в пределах Q=1÷30 л/с, кинематическом коэффициенте вязкости υ = 0,013 см2/с, если трубы неновые стальные.
6) Из бака при постоянном напоре Н по трубопроводу, имеющем уклон, характеризуемый следующими данными: отметка сечения 1-1 z1=4 м, сечения 4-4 z4=2 м, длиной I=100 м и диаметром D=0,1 м вытекает вода в атмосферу. На расстоянии I1=80 м от начала трубопровода установлен вентиль. Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии, если Н=6 м; λ=0,03.
Date: 2016-02-19; view: 3300; Нарушение авторских прав
Источник
d | c | z | d2 | H | z | z | d | c | z | d2 | |||
c | ( | ) ( | ) | c | |||||||||
D2 | D2 | ||||||||||||
H dc | dc | dc | dc | H dc | |||||||||
dc | ( l g) z | d2 | H z | z | dc | ( l g) z | |||||||
c | A( | ) ( | ) | ||||||||||
H | d | H | |||||||||||
l | d D2 | d d | см | l | d | ||||||||
c | c c | c | c | ||||||||||
H | z | ||
A( | ) | , | |
dc | dc | ||
(28.262) |
dc2 | H | z | (28.263 | ||
( | ) . | ||||
2 | d | d | ) | ||
D | c | ||||
c | |||||
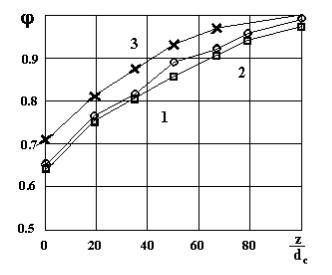
Известны опыты по определению концентраций в бугре с использовани-
ем метода отсечек. Полученные результаты показаны на рис. 28.2.
Рис. 28.2. Зависимость истинного газосодержания
от безразмерной высоты газожидкостного бугра и числа Фруда
1 – Fr = 19; 2 – Fr = 13; 3 – Fr = 8.4
Расчётная часть
1. По результатам видеосъёмки выполненной работы 27 составляют таблицу значений (для верхних и нижних оценок) истинного газосодержания
иплотностей смеси при пяти значениях безразмерной координаты бугра. Что-
-131 –
бы получить эти значения на экране телевизора останавливают одно из изображений истечения, снимают геометрические размеры бугра, производят вычисления левых и правых частей неравенств (28.262) и (28.263) и заполняют таблицу (форма 28.5).
2.По вычисленным значениям на экспериментальный график рис. 28.2 наносят соответствующие точки и соединяют линиями.
3.Рассчитывают число Фруда по формуле
Q | m | 2 | |
Fr | 2 | . | (28.264) |
ldc | gdc | ||
4. Рассчитывают для одних и тех же безразмерных координат отклонения верхних и нижних оценок от экспериментальных точек.
Форма 5 | ||||
№ | Величины | Вычислено | ||
1 | Высота бугра по результатам видеосъёмки, Н | |||
2 | Диаметр бугра по результатам видеосъёмки, D | |||
3 | Диаметр сопла, dc | |||
4 | Нижние оценки для (левая часть формулы | |||
(28.262)) при z=0, H/5, 2H/5, 3H/5, 4H/5, H | ||||
5 | Верхние оценки для (правая часть формулы | |||
(28.262)) при z=0, H/5, 2H/5, 3H/5, 4H/5, H | ||||
6 | Нижние оценки для | см | (левая часть формулы | |
(28.262)) при z=0, H/5, 2H/5, 3H/5, 4H/5, H | ||||
7 | Верхние оценки для | см | (правая часть формулы | |
(28.262)) при z=0, H/5, 2H/5, 3H/5, 4H/5, H | ||||
8 | Число Фруда, Fr | |||
9 | Оценки отклонений | |||
– 132 –
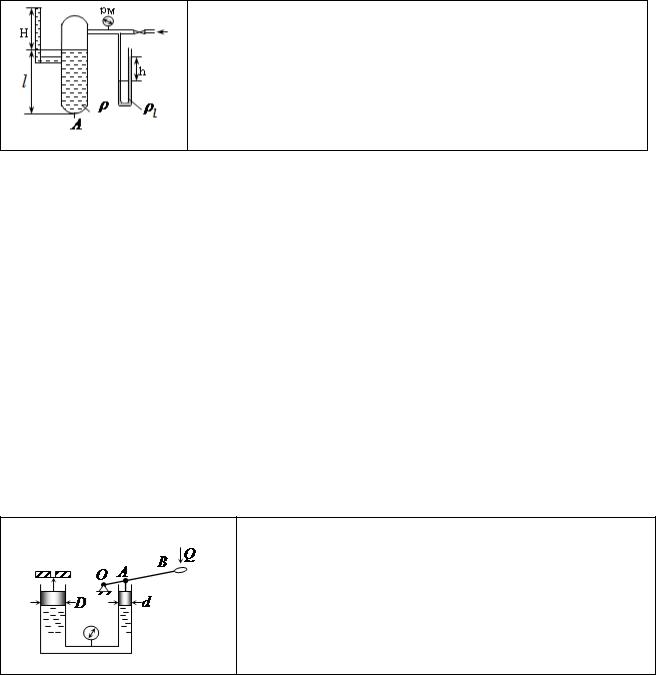
ПРИЛОЖЕНИЕ 1 ПРИМЕРЫ КОНТРОЛЬНЫХ КАРТ ДЛЯ ЗАЩИТЫ РАБОТ
1. Пример контрольной карты для защиты работ №№ 1, 2
Вопрос 1. По какому из выражений правильно определить величину рм?
1.рА gH рм ; 2. рА g(H ); 3. рА g рм 1gh ;
4.рА (H h) g ; 5. рА рм gH g .
Вопрос 2. Как изменится h, если в U – образный дифференциальный манометр залить ртуть l = рт ( рт – плотность ртути)?
1. Не изменится; 2. Увеличится в рт/ l раз; 3. Уменьшится в рт/ l раз;
4. Увеличится в / l раз; 5. Уменьшится в рт/ l раз.
Вопрос 3. Чему равно абсолютное давление воздуха рабс в сосуде, если известна величина H?
1. | рабс = gH; 2. рабс = gH + pатм; 3. рабс = gH + pм; |
4. | рабс = gH + pм + pатм; 5. рабс = l gH + pм. |
Вопрос 4. Как изменится выигрыш в силе на гидравлическом прессе, если давление в нем увеличится в 2 раза?
1. Не изменится; 2. Увеличится в 2 раза; 3. Уменьшится в 2 раза; 4. Увеличится в 4 раза; 5. Уменьшится в 4 раза.
Вопрос 5. Диаметр большого поршня увеличен в 2 раза. Как нужно изменить OBOA, чтобы выигрыш в силе остался неизменным?
1. Сделать ОА = ОВ; 2. Увеличить в 4 раза; 3. Уменьшить в 4 раза;
– 133 –
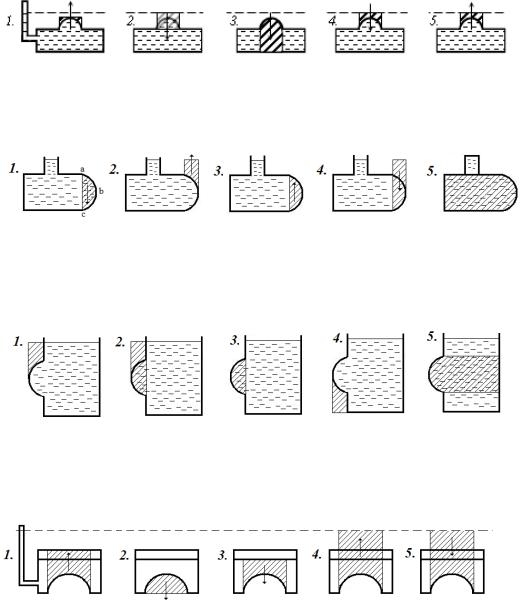
4.Увеличить в 2 раза; 5. Уменьшить в 2 раза.
2.Пример контрольной карты для защиты работ №№ 4 и 5
Вопрос 1. Построить «тело давления» и показать направление действия вертикальной составляющей силы давления жидкости для криволинейной поверхности.
Вопрос 2. Построить объем «тела давления» и показать направление действия вертикальной составляющей силы давления жидкости для криволинейной поверхности авс.
Вопрос 3. Полусферическая крышка расположена в боковой стенке открытого резервуара. Показать объем, с помощью которого определяется вертикальная составляющая силы давления жидкости на эту полусферическую крышку.
Вопрос 4. Построить «тело давления» и показать направление действия вертикальной составляющей силы давления жидкости для криволинейной поверхности.
Вопрос 5. Как связаны между собой давления в точках А и В жидкости, вращающейся с постоянной угловой скоростью?
– 134 –
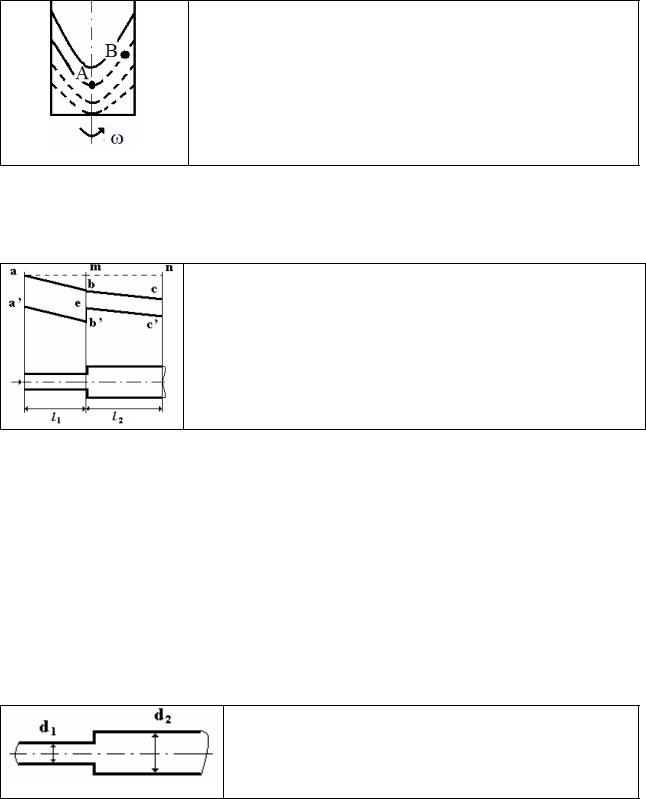
1. рА = рВ; 2. Нужно иметь определённые данные;
3. рА < рВ; 4. рА > рВ.
3. Пример контрольной карты для защиты работ №№ 7, 8, 9
Вопрос 1. На рисунке показаны линии полного и пьезометрического напоров (без учета местных сопротивлений). Для участков длиной l1 и l2 гидравлические уклоны определяются
1. | i1 mс / 1 , | i2 | nc / 2 /l2 ; | |
2. | i1 | mb/ 1 , | i2 | nc/ 2 ; |
3. | i1 | mb / 1, | i2 | (nc mb)/ 2 ; |
4. | i1 mb / 1, | i2 nc/ 2 ; | ||
5. | i1 | mb/ 1 , , | i2 (nc mb)/ 2 . | |
Вопрос 2. Может ли возрастать пьезометрический напор по направлению движения вязкой жидкости в потоке с горизонтальной осью?
1.Не может, как бы ни изменялась площадь по длине потока.
2.Может, если площадь сечения потока увеличивается по направлению движения.
3.Не может, так как из-за потерь энергии пьезометрический напор всегда падает.
4.Не может, так как труба горизонтальная.
5.Может, если площадь уменьшается по направлению движения.
Вопрос 3. Отношения диаметров участков трубопровода d1/d2 = 1/3. Каково отношение соответствующих скоростных напоров?
1. | 27; | 2. | 3; | ||
3. | 9; | 4. | 81; | 5. | 1/9. |
Вопрос 4. Какова средняя скорость во всасывающей линии центробежного насоса, если площадь ее живого сечения 20 см2 , а расход Q =10
л/с?
1. 0,5 м/с; 2. 5 м/c; 3. 50 м/с; 4. 25 м/с; 5. 2,5 м/с.
– 135 –
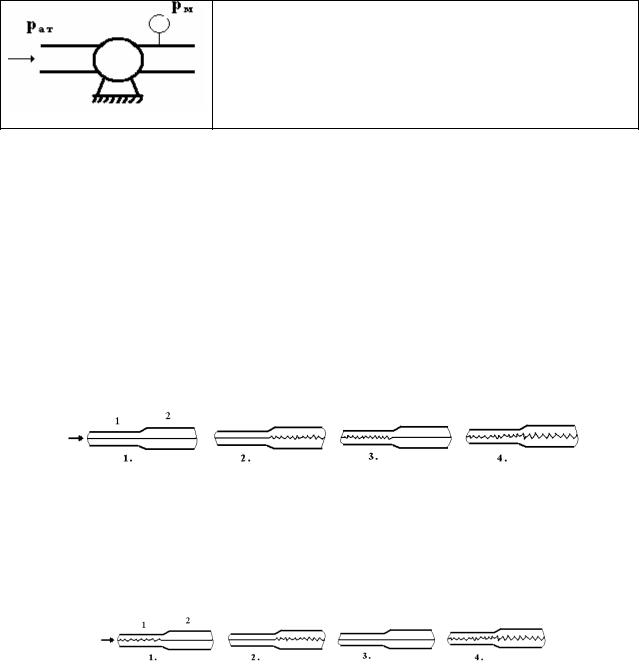
Вопрос 5. Параметры насоса: мощность(на валу) 4кВт, КПД = 80%. Каков будет расход при перекачке жидкости, если давление на входе ратм, а в начале нагнетательной линии манометр показывает рм = 200 кПа?
1. | 1,4 л/с; | 2. | 16 л/с; |
3. | 1,6 л/с; | 4. | 1,04 м3/с; |
5.0,16 м3/c
4.Пример контрольной карты для защиты работ №№ 11, 12
Вопрос 1. Как изменится величина критического расхода Qкр, если диаметр трубопровода увеличить в 2 раза?
1. Увеличится в 2 раза; | 2. Уменьшится в 4 раза; |
3. Останется прежней; | 4. Уменьшится в 2 раза. |
Вопрос 2. Как будет вести себя струйка чернил, если в 1 трубке режим движения ламинарный?
5. Ответ может быть дан, только если известна вязкость жидкости.
Вопрос 3. Какой вид примет чернильная струйка, если в 1 трубке число Re = 1000?
5. Ответ может быть дан только при известной вязкости протекающей жидкости.
Вопрос 4. Какой из приведенных графиков выражает закон распределения скоростей по живому сечению потока идеальной жидкости при установившемся течении в круглой трубе?
– 136 –

Вопрос 5. Как определяется расход жидкости в работе № 11?
1.Отношением количества истекающей жидкости ко времени ее движения.
2.Отношением объемного расхода к площади живого сечения.
3.По показаниям трубки Пито-Прандтля.
4.По показаниям дифференциального манометра.
5.По формуле 2gH.
5.Пример контрольной карты для защиты работы № 13
Вопрос 1. При течении вязкой жидкости в шероховатой трубе показания дифференциального манометра уменьшается, если остальные параметры остаются неизменными:
1. t0 – уменьшить; | 2. Q – | увеличить; |
3. d – уменьшить; | 4. ρ2 | – уменьшить; |
5. t0 – увеличить. | ||
Вопрос 2. Течение жидкости ламинарное. Как изменятся потери на участке, если l увеличить в 2 раза, а расход уменьшить в 2 раза?
1.Увеличатся в 2 раза; 2. Уменьшатся в 2 раза;
3.Останутся неизменными;
4.Увеличатся в 4 раза;
5.Уменьшатся в 8 раз.
Вопрос 3. Каково соотношение между показаниями ртутного дифференциального манометра (h) и пьезометра (H) при течении воды?
1. H/h=13,6 ; | ||
2. | H/h=12,6 ; | |
3. | H/h=1/13,6 ; | |
4. | H/h=1/12,6 ; | 5. H=h . |
– 137 –

Вопрос 4. Коэффициент гидравлического сопротивления λ связан функциональной зависимостью:
1. λ=λ(Re,L) ; | 2. | λ=λ(Δ,d) ; | 3. λ=λ(Re, Δ/d) ; |
4. λ=λ(Re,d) ; | 5. | λ=λ(Re, Δ/L) . |
Вопрос 5. При уменьшении диаметра и сохранении расхода:
1.Уменьшатся потери на участке 1-2;
2.Увеличатся потери на участке 1-2;
3.Потери на участке 1-2 не изменятся;
4.Уменьшится давление в сечении 1;
5.Уменьшится разность давлений между сечениями 1 и 2.
6.Пример контрольной карты для защиты работ № 16
Вопрос 1. Какой максимальный вакуум может образоваться в сжатом сечении струи внутри насадка?
1. 1 атмосфера; 2. рн.с. – давление насыщенных паров; 3. ратм – рн.с.; 4. 0,5 атм.
Вопрос 2. Формула для теоретической скорости истечения vт плучена при следующих предположениях и имеет вид
1. | Жидкость считается идеальной, vт = ·(2gH)0/5; | |
2. | Жидкость считается вязкой, | vт = (2gH)0/5; |
3.Жидкость считается вязкой, vт = ·(2gH)0/5;
4.Жидкость считается идеальной, vт = (2gH)0/5.
Вопрос 3. В лабораторной работе Вы определяете коэффициенты скорости и расхода цилиндрического насадка , следующим образом
1.= · , определяется с помощью значений x и y траектории струи при помощи координатной сетки;
2.= Q/QТ, = / ;
3.определяется через измерение действительного расхода Q и вычисле-
ние теоретического расхода QТ, = / ;
4. = Q/QТ, определяется с помощью значений x и y траектории струи при помощи координатной сетки.
5.
Вопрос 4. При определении времени опорожнения резервуара принимаются следующие предположения
1.Движение считается установившимя ( зависит от числа Re);
2.Движение в течение всего времени опорожнения считется установив-
шимя ( = const);
– 138 –

3. Используют гипотезу последовательной смены стационарных состояний
( = const).
Вопрос 5. Найти отношение расходов при истечении из отверстий
1. Q1/Q2 = 1;
2. Q1/Q2 = d1H20,5/ d2 H10,5; 3. Q1/Q2 = d12H1/ d2 2H2;
4. Q1/Q2 = (d1/d2 )(H2 – H1)0,5 ; 5. Q1/Q2 = (d1/d2 )2 (H1/H2 )0,5
7. Пример контрольной карты для защиты работы № 18
Вопрос 1. Напорную емкость 1 подняли выше. Остальные условия опыта остались неизменными. Как изменится величина ударного давления?
1.Не изменится; 2. Увеличится, т.к. увеличится с;
3. Уменьшится, т.к. уменьшится с; 4. Уменьшится, т.к. уменьшится υ;
5.Увеличится, т.к. увеличится υ.
Вопрос 2. Напорную емкость 1 установили ниже. Остальные условия остались неизменными. Как изменится величина ударного давления?
1. Не изменится; 2. Увеличится, т.к. увеличится υ; 3. Уменьшится, т.к. уменьшится υ; 4. Уменьшится, т.к. уменьшится с; 5. Увеличится, т.к. увеличится с.
Вопрос 3. Величина ударного давления увеличится, если:
1. Диаметр трубопровода уменьшить; | 2. Длину трубы увеличить; | |
3. | Плотность жидкости уменьшить; | 4. Толщину стенок трубы умень- |
шить; | 5. Модуль упругости жидкости уменьшить. | |
Вопрос 4. На какой из осциллограмм правильно показано время двойного пробега ударной волной расстояния L от датчика до начала трубопровода?
– 139 –
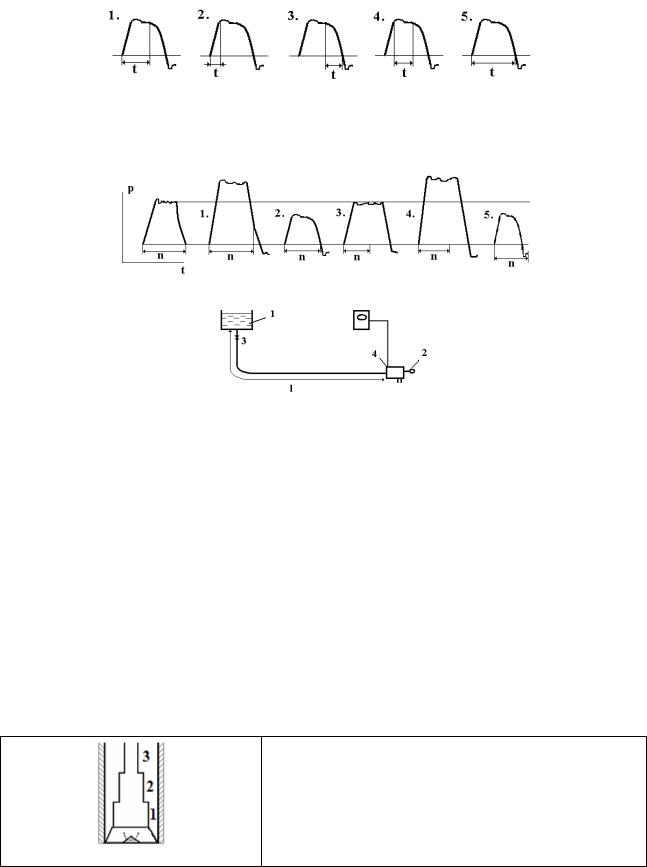
Вопрос 5. Как изменится осциллограмма, если расход жидкости уменьшится?
8. Пример контрольной карты для защиты работы № 19
Вопрос 1. Режим течения турбулентный. Во сколько раз скорость витания частицы размером dч=5 мм будет отличаться от скорости для частицы dч=20 мм при прочих равных условиях?
1. В 0,5 раза; 2. В 2 раза; 3. В 4 раза; 5. равны
Вопрос 2. Расчетным путем получено, что из скважины при бурении выносятся частицы из кольцевого пространства 2 (см.рисунок). Будут ли выносится частицы того же диаметра из других затрубных пространств?
1. Будут из 1 и 3;
2. Будут из 1 и 2;
3. Будут из 1, 2 и 3;
4. Будут из 3 и не будут из 1;
5. Будут из 1 и не будут из 3.
Вопрос 3. Частица витает в потоке жидкости. Если плотность жидкости уменьшить, не изменяя других параметров, то как поведет себя частица?
– 140 –
Источник
В U-образный сосуд налиты ртуть и вода. Линия раздела жидкостей расположена ниже свободной поверхности ртути на hpт=2 см. Определить разность уровней h в обеих частях сосуда.
Дано:
ρводы=1000 кг/м3;
ρртути=13600 кг/м3;
hрт=2 см =0,02 м.
Определить:
H
Решение:
Запишем уравнение для определения абсолютного гидростатического давления на уровне раздела жидкостей в левом колене U-образного сосуда:
(1)
где ра – атмосферное давление на свободной поверхности воды в левом колене U-образного сосуда, Па;
ρвghв – вес столба воды высотой hв, Па.
В правом колене на этом уровне абсолютное гидростатическое давление определяется по следующему выражению:
(2)
где ра атмосферное давление на свободной поверхности ртути в правом колене U-образного сосуда, Па;
ρpтghpт – вес столба ртути высотой hpт, Па.
Так как абсолютное гидростатическое давление на выбранном уровне в правом и левом колене U-образного сосуда будет одинаковым, то уравнения (1) и (2) можно приравнять:
Вариант №1
1) Уровень мазута в вертикальном цилиндрическом баке диаметром 2 м за некоторое время понизился на 0,5 м. Определить массу израсходованного мазута, если плотность его при температуре окружающей среды 20 °С равна ρ=990 кг/м3.
2) Найти давление на свободной поверхности в закрытом сосуде с бензином, если уровень жидкости в открытом пьезометре выше уровня жидкости в сосуде на h=2 м, а атмосферное давление ра=100 кПа.
3) Определить величину силы гидростатического давления воды на вертикальный щит шириной b=2 м, если глубина воды перед щитом Н=2,7 м.
4) Определить давление p1 в сечении 1-1 горизонтально расположенного сопла, необходимое для придания скорости воде в выходном сечении 2-2 V2=40 м/с (р2= ра), если скорость движения воды в сечении 1-1 V1=3 м/с.
5) Построить график зависимости коэффициента гидравлического трения λ от числа Рейнольдса в водопроводной трубе D=150 мм при расходе, изменяющемся в пределах Q=1÷30 л/с, кинематическом коэффициенте вязкости υ = 0,013 см2/с, если трубы асбестоцементные.
6) Из бака при постоянном напоре Н по трубопроводу, имеющем уклон, характеризуемый следующими данными: отметка сечения 1-1 z1=5 м, сечения 4-4 z4=3 м, длиной I=100 м и диаметром D=0,1 м вытекает вода в атмосферу. На расстоянии I1=80 м от начала трубопровода установлен вентиль. Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии, если Н=5 м; λ=0,03.
Вариант №2
1) Уровень мазута в вертикальном цилиндрическом баке диаметром 1,8 м за некоторое время понизился на 1 м. Определить массу израсходованного мазута, если плотность его при температуре окружающей среды 20°С равна ρ=990 кг/м3.
2) В U-образный сосуд налиты ртуть и вода. Линия раздела жидкостей расположена ниже свободной поверхности ртути на hpт=8 см. Определить разность уровней h в обеих частях сосуда.
3) Определить силу давления воды на дно сосуда и на каждую из четырех опор. Собственным весом сосуда пренебречь.
4)Определить давление p1 в сечении 1-1 трубопровода, необходимое для придания скорости воде в сечении 2-2 V2=20 м/с (р2=90 кПа) если скорость движения воды в сечении 1-1 V1=5 м/с.
5)Построить график зависимости коэффициента гидравлического трения λ от числа Рейнольдса в водопроводной трубе D=150 мм при расходе, изменяющемся в пределах Q=1÷30 л/с, кинематическом коэффициенте вязкости υ = 0,013 см2/с, если трубы неновые стальные.
6) Из бака при постоянном напоре Н по трубопроводу, имеющем уклон, характеризуемый следующими данными: отметка сечения 1-1 z1=4 м, сечения 4-4 z4=2 м, длиной I=100 м и диаметром D=0,1 м вытекает вода в атмосферу. На расстоянии I1=80 м от начала трубопровода установлен вентиль. Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии, если Н=6 м; λ=0,03.
Источник
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
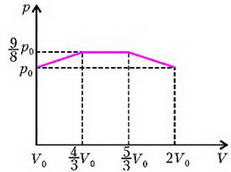
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
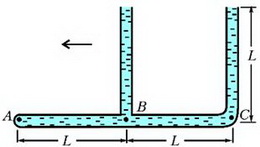
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
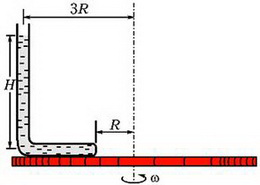
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
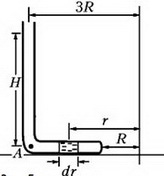
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
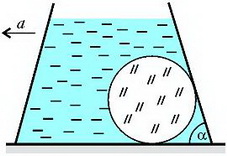
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
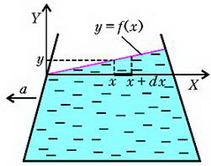
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде —
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
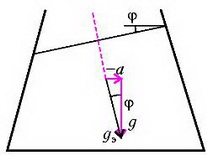
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
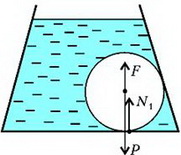
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
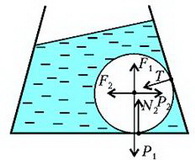
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с не?
