Как изменяются величины при охлаждении сосуда с идеальным газом

КПД тепловой машины.
Если понизить температуру холодильник при неизменной температуре нагревателя, КПД идеальной тепловой машины увеличится.
Формулы для КПД тепловой машины
η=(1-Tх/Tн)*100% – зависимость КПД тепловой машины от температуры нагревателя и холодильника.
η=((Тн-Тх)/Тн)*100% – развёрнутая формула.
В абсолютном смысле, КПД связан с работой газа А и количеством теплоты Q, полученным газом за цикл, соотношением: η=(A/Q)*100%
Qхол=Q-A
Qхол – количество теплоты, отданное холодильнику.
Поскольку при понижении температуры холодильника количество теплоты, полученное газом от нагревателя за цикл, не изменяется, заключаем, что работа газа за цикл увеличивается. Отданное количество теплоты холодильнику можно найти, вычитая из количества затраченной теплоты совершённую работу. Если повысить температуру холодильника при неизменной температуре нагревателя, КПД идеальной тепловой машины уменьшится (см. формулу в рамке слева).
КПД связан с работой газа и количеством теплоты, полученным газом за цикл, отношением количества совершённой работы к количеству затраченной теплоты. Таким образом, при повышении температуры холодильника работа газа за цикл уменьшится. Количество теплоты, отданное холодильнику, увеличится.
Совершённой за цикл механической работе тепловой машины на диаграмме p-V соответствует площадь внутри цикла на диаграмме. Если площадь двух равных циклов одинакова, значит одинакова и работа, совершённая в этих циклах. При увеличении давления, а также при увеличении объёма неизменного количества газа, его температура увеличивается. И напротив, при уменьшении объёма, а также при уменьшении давления, температура тоже уменьшается.
При изохорном увеличении давления температура газа увеличивается так, что всё поступающее от нагревателя тепло, расходуется на увеличение внутренней энергии, без совершения работы: Q=ΔU=(3/2)vRΔT.
При изобарном уменьшении объёма, всё поступающее тепло расходуется на увеличение объёма, без изменения внутренней энергии: Q=A=p0(V2-V1). Если в результате изменения цикла работа газа не изменяется, а передаваемое от нагревателя количество теплоты увеличивается, то КПД тепловой машины уменьшается.
Характеристики газа в закрытом сосуде
Для газа в герметично закрытом сосуде соблюдаются законы изохорных процессов. При изохорном охлаждении давление газа уменьшается, так как уменьшается кинетическая энергия молекул, а объём не меняется. Плотность газа не изменяется, так как не меняется объём, занимаемый газом, и не изменяется количество газа. Внутренняя энергия, как было отмечено, уменьшается, так как для фиксированного количества вещества зависит только от его температуры.
Внутренняя энергия газа
U=(i/2)vRT, где i – число степеней свободы газа.
Если же газ из сосуда выпускать или выкачивать наружу, то его количество в сосуде будет уменьшаться. Значит давление в сосуде будет уменьшаться, так как прежний объем занимает меньшее количество газа. Внутренняя энергия содержимого уменьшится, так как уменьшится количество молекул, а именно они и являются носителями этой энергии. Температура не изменится, если с внешней средой будет установлено тепловое равновесие (сначала температура снизится по идее, но потом извне поступит тепло). Если же сказано, что после выпускания газа давление в сосуде осталось неизменным, а плотность и количество уменьшились, значит была увеличена температура газа.
При изохорном нагревании концентрация молекул газа не изменяется; внутренняя энергия увеличивается, поскольку для фиксированного одноатомного идеального газаона зависит только от температуры: ΔU=(3/2)vRT. Поскольку объём фиксирован, теплоёмкость зависит только от количесвта теплоты и изменения температуры: c=Q/ΔT=ΔU/ΔT, так как всё поступающее тепло расходуется только на изменение внутренней энергии, ведь газ не совершает работу. В итоге все величины, от которых зависит теплоёмкость, в данном случае не изменяются, а значит и теплоёмкость не изменяется.
При изохорном уменьшении температуры, давление газа уменьшается, объём не изменяется, внутренняя энергия уменьшается. Внутренняя энергия в данном случае зависит только от температуры.
В изохорном процессе при неизменном количестве вещества, по закону Шарля, p/T=const.
Характеристика газа с постоянным давлением
Процессы, происходящие при постоянном давлении, называются изобарными.
При изобарном нагреванииV/T=const, значит объём газа увеличивается. Плотность обратно пропорциональна объёму и, так как количество газа не меняется, плотность газа уменьшается. Внутренняя энергия с увеличением температуры увеличивается.
При изобарном процессе, давление газа не меняется, при увеличении температуры объём увеличивается.
в изобарном процессе при неизменном количестве вещества,по закону Гей-Люссака, V/T=const.
Изотермические процессы
При изотермическом расширении температура газа остаётся неизменной, объём газа увеличивается, давление газа уменьшается, поскольку в изотермических процессах величина pV не изменяется, так как pV~T, T=const.
В изотермическом процессе при неизменном количестве вещества по закону Бойля-Мариотта, pV=const.
Адиабатические процессы
При адиабатическом увеличении объёма сосуда, температура уменьшается. Дело в том, что при расширении газ совершает работу, теплообмен с внешней средой отсутствует ,а значит внутренняя энергия уменьшается: Q=ΔU+A; ΔU=-A, т.к. Q=0 при адиабатическом процессе. Температура газа зависит только от его внутренней энергии, а значит, уменьшается. Объём увеличивается, а количество молекул газа не изменяется, а значит уменьшается концентрация: n=N/V. Давление связано с концентрацией молекул и температурой соотношением p=nKT. Таким образом, при адиабатическом увеличении объёма, давление уменьшится.
Внутренняя энергия, работа, температура
Согласно первому началу термодинамики, переданное газу количество теплоты идёт на изменение его внутренней энергии, а также на совершение газом работы против внешних сил: Q=ΔU+A.
Всё переданное газу количество теплоты идёт на совершение газом работы при изотермическом процессе, так как при постоянной температуре внутренняя энергия не изменяется. При изохорном процессе изменение внутренней энергии газа равно количеству переданной теплоты, так как при постоянном объёме газ не совершает работу.
При совершении газом положительной работы, его объём увеличивается, давление уменьшается (при изотермическом процессе), внутренняя энергия не изменяется.
Согласно первому началу термодинамики, внутреннюю энергию тела можно изменить, совершая над газом работу или передавая ему тепло. При плавлении льда, его температура не изменяется, а внутренняя энергия увеличивается. При выделении же тепла, внутренняя энергия вещества уменьшается. При кристаллизации воды, её температура не меняется, а внутренняя энергия уменьшается: Q=λm.
Температура при плавлении остаётся постоянной, поэтому постоянной будет и средняя кинетическая энергия движения молекул, но изменяется потенциальная энергия их взаимодействия. Следовательно, изменяется и сумма всех кинетических и потенциальных энергий всех молекул (внутренняя энергия). Из-за изменения взаимодействия молекул при кристаллизации уменьшается внутренняя энергия, а при плавлении – увеличивается.
Внутренняя энергия одноатомного идеального газа связана с его температурой соотношением U=(3/2)vRT. Следовательно, температура равна T=2U/(3vR). Давление, температура и занимаемый газом объём не независимы, они связаны уравнением состояния Менделеева-Клапейрона: pV=vRT. Таким образом, давление газа равно p=vRT/V=(2/3)*(U/V).
При изотермическом процессе, температура остаётся неизменной, поэтому внутренняя энергия идеального газа не меняется, а значит, согласно первому началу термодинамики, всё переданное тепло полностью превращается в работу.
При изобарном процессе, давление не изменяется, но меняются как температура, так и объём газа, а значит при передаче газу тепла в данном процессе, газ совершает работу, нагреваясь при этом, то есть кроме совершения работы, происходит увеличение внутренней энергии.
При изохорном процессе объём газа фиксирован, значит газ не может совершать работу, следовательно всё поступающее тепло идёт на увеличение внутренней энергии.
При постоянном давлении изменение внутренней энергии прямо пропорционально изменению объёма газа, так как внутренняя энергия напрямую зависит от температуры. Внутренняя энергия уменьшается с потерей температуры. Если изменение внутренней энергии положительно, значит абсолютная температура тела уменьшилась.
Теплоёмкость газа постоянна.
Насыщенный пар
При изотермическом уменьшении объёма сосуда с насыщенным паром, давление в сосуде не изменяется, масса конденсированной воды увеличивается, масса пара уменьшается. Это объясняется тем, что в данном процессе пар конденсируется и его концентрация не изменяется, но уменьшается объём (давление не меняется в отсутствии воздуха; в присутствии воздуха, суммарное давление газов увеличивается, парциальное давление пара не изменяется, парциальное давление воздуха увеличивается).
Сосуд с поршнем
Давление поршня на газ
p=mg/S
m – масса поршня;
g – ускорение свободного падения;
s – площадь поршня
Если система находится под атмосферным давлением, то давление газа под поршнем равно сумме давление поршня и атмосферного давления
При добавлении газа в сосуд с подвижным свободным поршнем, объём газа увеличивается, давление не изменяется. Поршень находится в равновесии, а значит pатмS+mg=pгазаS, так как поршень покоится. Увеличение количества вещества при неизменной температуре и давлении приведёт к увеличению объёма. Архимедова сила определяется плотностью среды, в которую помещено тело: FA=ρgVтела. Поскольку плотность газа не изменяется, сила Архимеда тоже неизменна.
При охлаждении газа под свободным поршнем, объём газа уменьшается, так как идёт изобарный процесс. Давление не изменится, а Архимедова сила, действующая на тело, находящееся в сосуде, увеличится, так как при уменьшении объёма количество газа осталось прежним, значит концентрация увеличилась, следовательно, увеличилась плотность газа, а сила Архимеда с увеличением плотности, увеличилась.
В газе, находящемся под свободным поршнем все процессы происходят изобарически. Переданное тепло идёт на работу газа против внешних сил, а также на увеличение внутренней энергии, а значит и температуры.
В результате изобарного расширения, да и вообще любого расширения газа, с фиксированным количеством вещества, концентрация молекул уменьшается.
Испарение жидкости
Испарение жидкости, в отличие от кипения, происходит при любой температуре. Процесс испарения воды представляет собой вылет молекул воды с поверхности жидкости. При этом преимущественно вылетают самые быстрые молекулы, и средняя кинетическая энергия движения молекул воды в сосуде уменьшается, а значит, уменьшается и температура жидкости, что можно подтвердить с помощью термометра (данный эффект используется для измерения влажности окружающего воздуха при помощи психрометра). Присутствует и обратный процесс, конденсация, но при относительной влажности воздуха ниже 100% процесс испарения преобладает. Если относительная влажность воздуха равна 100%, то количество испаряющихся в единицу времени молекул равно количеству конденсирующихся, а значит в среднем в сосуде количество молекул не изменяется. Если относительная влажность воздуха менее 100%, то количество молекул в сосуде постепенно уменьшается, а значит уменьшается внутренняя энергия и температура воды. При плавлении и кипении же температура не изменяется, но изменяется внутренняя энергия вещества. При испарении без кипения, чтобы молекулы жидкости переходили из жидкого состояния в газообразное, им тоже нужна добавка к энергии, которая идёт за счёт уменьшения средней энергии движения оставшихся молекул, в результате чего температура жидкости уменьшается.
при испарении жидкости без кипения, температура пара увеличивается, а температура жидкости уменьшается.
Тепловое равновесие
При установлении теплового равновесия, температуры всех тел сравниваются. Внутренние энергии тел разной температуры при тепловом контакте изменяются: внутренняя энергия горячего ела уменьшается, а холодного – увеличивается. Суммарная внутренняя энергия замкнутой системы не изменяется (по закону сохранения энергии).
Изохорный процесс
При постоянном объёме с увеличением внутренней энергии давление увеличивается прямо пропорционально.
Плавление и кристаллизация
Если 1 кг льда при температуре 0°С передать 330 кДж энергии (удельная теплота плавления льда равна 330 кДж/кг), то вся энергия будет израсходована на плавление, весь лёд растает. При этом его температура не изменится, внутренняя энергия увеличится, объём уменьшится. при кристаллизации же напротив, внутренняя энергия уменьшится, температура не изменится, объём увеличится.
Если в тёплую воду погрузить кусок льда, то когда он растает, уровень воды не изменится по сравнению с тем, что был тогда, когда погрузили лёд, так как несмотря на то, что объём льда уменьшился, его плотность была меньше, чем у воды, и он плавал на поверхности, вытесняя такой объём жидкости, который потом сам займёт, когда растает.
Источник
12. МКТ и Термодинамика (изменение физических величин в процессах, установление соответствия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В цилиндрическом сосуде под поршнем находится газ. Поршень не закреплён и может перемещаться в сосуде без трения (см. рисунок). Газ медленно охлаждают. Как изменятся в результате этого давление газа и концентрация его молекул?

Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Давление газа}&text{Концентрация}\
&text{молекул газа}\
hline
&\
hline
end{array}]
“Демоверсия 2019”
Поскольку поршень не закреплён и может перемещаться в сосуде без трения, давление газа не изменится. При охлаждении объём газа уменьшится, значит, его концентрация увеличится.
Ответ: 31
Идеальный газ совершает два процесса. В процессе 1 газ сначала нагревался при постоянном давлении, потом его давление увеличивалось при постоянном объеме, затем при постоянной температуре давление газа уменьшилось до первоначального значения. В процессе 2 объем газа с давлением сначала увеличивались, затем его объем уменьшался при постоянном давлении, потом давление газа уменьшалось при постоянном объеме и газ вернулся в первоначальное состояние. Какие из графиков в координатных осях (p – V) соответствует этим изменениям состояния газа? 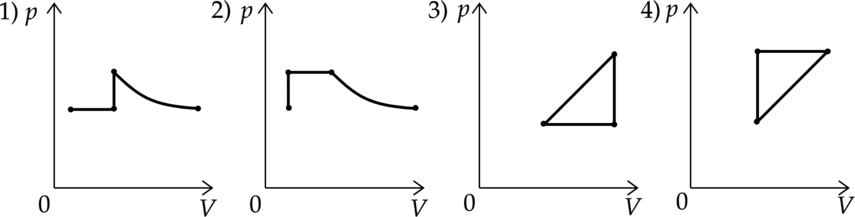
Запишите в таблицу выбранные цифры для каждого процесса в указанном порядке. [begin{array}{|c|c|c|}
hline
text{ Процесс } 1&text{ Процесс }2\
hline
&\
hline
end{array}]
Распишем, как должны выглядеть процессы в координатах (p-V).
Процесс 1:
Газ сначала нагревался при постоянном давлении, значит на графике это будет горизонтальная прямая. Потом его давление увеличивалось при постоянном объеме — это будет вертикальная прямая. Затем при постоянной температуре давление газа уменьшилось до первоначального значения — на графике это будет гипербола.
Нам подходит первый вариант.
Процесс 2:
Объем газа с давлением сначала увеличивались, значит на графике это прямая, направленная под углом к осям. Затем его объем уменьшался при постоянном давлении — на графике это будет горизонтальная прямая. Потом давление газа уменьшалось при постоянном объеме – это будет вертикальная прямая.
Нам подходит график 4.
Ответ: 14
Идеальный газ совершал два процесса. В процессе 1 газ сначала охлаждался при постоянном давлении, потом его давление уменьшалось при постоянном объеме, затем при увеличении температуры давление газа увеличилось до первоначального значения. В процесс 2 газ сначала давление газа уменьшалось при постоянной температуре, потом газ расширялся при постоянном давлении, затем увеличивал давление до первоначального, при постоянном объеме. Какие из графиков в координатных осях (p-V) соответствует этим изменениям состояния газа? 
Запишите в таблицу выбранные цифры для каждого процесса в указанном порядке. [begin{array}{|c|c|c|}
hline
text{ Процесс } 1&text{ Процесс }2\
hline
&\
hline
end{array}]
Распишем, как должны выглядеть процессы в координатах (p-V).
Процесс 1:
Газ сначала охлаждался при постоянном давлении — горизонтальная прямая. Потом его давление уменьшалось при постоянном объеме — вертикальня прямая. Затем при увеличении температуры давление газа увеличилось до первоначального значения — прямая, направленная под углом к осям.
Это график 4.
Процесс 2:
Сначала давление газа уменьшалось при постоянной температуре — гипербола. Потом газ расширялся при постоянном давлении — горизонтальная прямая. Затем увеличивал давление, до первоначального, при постоянном объеме — вертикальная прямая.
Таким образом, нам подходит вариант 1.
Ответ: 41
В сосуде неизменного объема находится идеальный газ. Часть газа выпускали из сосуда так, что давление оставалось неизменным. Как изменились при этом температура газа, оставшегося в сосуде, и количество вещества?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|c|}
hline
text{ Температура газа}& text{ Количество вещества}\
hline
& \
hline
end{array}]
Температура — 1
1)Уравнение состояния газа: [pV=nu RT,] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества газа, (R) — универасальная газовая постоянная, (T) — абсолютная температура.
Выразим температуру газа: [T=dfrac{pV}{nu R}] При уменьшении количества газа ((V=const), (p=const)) температура увеличится.
Количество вещества — 2
2) Так как из сосуда выпустили часть газа, то количество вещества уменьшилось.
Ответ: 12
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменится в результате этого объём газа и его давление?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться. [begin{array}{|c|c|c|}
hline
text{ Объем газа}&text{ Давление}\
hline
&\
hline
end{array}]
Объем газа — 2
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлении. Уравнение состояния газа: [pV=nu RT,] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества газа, (R) — универасальная газовая постоянная, (T) — абсолютная температура.
Выразим отсюда объем газа: [V=dfrac{nu RT}{p}] При уменьшении количества вещества газа ((T=const), (p=const)) его объем уменьшится.
2) Давление — 3
Ответ: 23
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменится в результате этого объём газа и действующая на шарик архимедова сила?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|c|}
hline
text{ Объем газа}&text{ Сила Архимеда, действующая на шарик}\
hline
&\
hline
end{array}]
Объем газа — 2
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлении. Уравнение состояния газа: [pV=nu RT,] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества газа, (R) — универасальная газовая постоянная, (T) — абсолютная температура.
Выразим отсюда объем газа: [hspace{5 mm} V=dfrac{nu RT}{p} hspace{5 mm} (1)] При уменьшении количества вещества газа ((T=const), (p=const)) его объем уменьшится.
Сила Архимеда — 3
2) Сила Архимеда: [F_{text{Арх}}=rho gV_{text{ш}},] где (rho) — плотность газа, (g) — ускорение свободного падения, (V_{text{ш}}) — объем шарика.
Плотность газа по определению равна: [hspace{5 mm} rho = dfrac{m}{V}, hspace{5 mm} (2)] где (m) — масса газа.
Подставим (1) в (2) с учетом того, что (nu = dfrac{m}{mu}), где (mu) — молярная масса газа: [rho = mcdotdfrac{p}{RT}cdotdfrac{mu}{m} hspace{3 mm} Rightarrow hspace{3 mm} rho=dfrac{pmu}{RT}] Плотность газа не изменится и сила Архимеда, следовательно, тоже.
Ответ: 23
В закрытом сосуде находится идеальный газ. Как при охлаждении сосуда с газом изменятся величины: давление газа и его плотность?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|c|}
hline
text{ Давление газа}&text{ Плотность}\
hline
&\
hline
end{array}]
1) Уравнение состояния газа: [pV=nu RT,] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества газа, (R) — универасальная газовая постоянная, (T) — абсолютная температура.
Выразим отсюда давление: [p=dfrac{nu RT}{V}] Так как (V=const), а температура уменьшается, значит, давление газа уменьшается (изохорный процесс).
2) Плотность газа: [rho=frac{m}{V},] где (m) — масса газа.
Так как никакие величины не изменяются, то плотность газа также остается неизменной.
Ответ: 23
Источник
