Как найти диаметр сосуда формула

Что такое вместимость сосуда

Вместимость сосуда – это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ – кубический метр, но в случае жидкости чаще используют литр.

Особенности расчета объема жидкости в сосуде

Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества – твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.

В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.

Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.

За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:

(h = frac{p}{rho s g}.)

(p) здесь – давление в паскалях, (rho) – плотность, (g) – ускорение свободного падения, константа.

Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.

При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов.

Задача

Найти объем керосина, зная массу одного и того же сосуда с ним, и без него. Масса пустого сосуда 440 грамм, полного – 600 грамм.

Решение:

Плотность керосина можно узнать из справочной таблицы – 800 (frac{кг}{м^{3}}.)

Вычислим массу керосина в сосуде: 600 – 440 = 160.

Подставим известные данные в формулу:

(V = frac{m}{rho} = frac{0,16}{800} = 0,0002 м^{3} = 200 см^{3}.)

Ответ: 200 (см^{3}.)

Как определить вместимость сосудов разных форм

Вычисление объема параллелепипеда

Параллелепипед – это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.

(V = S_{осн} s H. )

Прямоугольный параллелепипед – это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, – это куб.

Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:

(V = AB s AD s AA_{1} = abc.)

Объем куба равен кубу его стороны:

(V = a^{3}.)

Нахождение объема пирамиды

Пирамида – это многогранник, состоящий из основания – плоского многоугольника, вершины – точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды – это перпендикуляр, опущенный из вершины на плоскость основания.

(V = frac{1}{3} s S_{осн} s h.)

Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований – (S_{1}) и (S_{2}).

(V = frac{1}{3} s h s (S_{1} + S_{2} + sqrt{S_{1} s S_{2}}). )

Как найти объем цилиндра

Цилиндр – это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

(R) – радиус основания цилиндра, (h) – его высота, равная образующей оси.

(V = S_{осн} s h = pi s R^{2} s h.)

Если нужно найти объем усеченного цилиндра, то понадобится не только R – радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l – (l_{1}) и (l_{2}).

(V = pi s R^{2} s frac{l_{1} + l_{2}}{2}.)

Как высчитать объем конуса

Конус – это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.

(V = frac{1}{3} s S_{осн} s h = frac{1}{3} s pi s R^{2} s h.)

Чтобы найти объем усеченного конуса, понадобятся (R_{1}) и (R_{2}) – радиусы оснований, а также высота (h).

(V = frac{pi s h}{3} s (R_1^2 + R_2^2 + R_1 s R_2).)

Нахождение объема шара

Шар – это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.

(R) – радиус полукруга, равный радиусу шара.

(V = frac{4pi s R^{3}}{3}.)

Источник

2 октября 2011

Автор КакПросто!

Объем определяет величину пространства, которую занимает какое-либо тело. Эта величина связана постоянными соотношениями с другими характеристиками физических тел – их геометрическими размерами, весом и плотностью. Поэтому измерение этих дополнительных параметров может стать базой для вычисления объема, например, сосуда.

Инструкция

Если есть возможность наполнить сосуд водой, то для определения его объема достаточно иметь какую-либо мерную форму. В зависимости от размеров сосуда мерной посудой может стать шприц, мензурка, стакан, банка, ведро или любая другая посуда, вместимость которой вам известна. Подобрав подходящий измерительный сосуд, заполните водой до краев сосуд исследуемый, а затем переливайте воду в измерительный сосуд, отсчитывая таким образом объем.

Если заполнить исследуемый сосуд жидкостью нет возможности, но можно поместить его в жидкость, то определите объем по количеству вытесненной им воды. Для этого тоже потребуется какая-либо мерная посуда. Заполнив ее частично водой, отметьте уровень, затем поместите в мерную посуду исследуемый сосуд таким образом, чтобы он полностью оказался под водой, и сделайте вторую отметку. Затем определите разницу объемов мерной посуды по разнице двух сделанных отметок.

Если мерной посуды нет, но есть возможность взвешивать сосуд, то определите разницу между сосудом пустым и заполненным водой. Исходя из того, что один кубический метр объема должен вмещать воду, весом в одну тонну, рассчитайте объем сосуда.

Если сосуд имеет геометрически правильную форму, то его объем можно рассчитать, измерив размеры. Для нахождения объема сосуда цилиндрической формы (например, кастрюли) надо измерить диаметр (d) его основания (дна кастрюли) и ее высоту (h). Объем (V) будет равен одной четверти от произведения возведенного в квадрат диаметра на высоту и число Пи: V=d²∗h∗π/4.

Для нахождения объема сосуда, имеющего форму шара, достаточно определить его диаметр (d). Объем (V) будет равен одной шестой части от произведения возведенного в куб диаметра на число Пи: V=d³∗π/6. Если измерить длину окружности (L) шарообразного сосуда в самой широкой его части проще (например, с помощью сантиметра), чем измерить диаметр, то объем можно рассчитать и через эту величину. Возведенную в куб длину окружности надо разделить на увеличенное в шесть раз число Пи, возведенное в квадрат: V=L³/(π²∗6).

Для нахождения объема (V) сосуда прямоугольной формы, надо измерить его длину, ширину и высоту (a, b и h) и перемножить полученные значения: V=a∗b∗h. Если этот сосуд имеет кубическую форму, то достаточно возвести длину одного его ребра в третью степень: V=a³.

Войти на сайт

или

Забыли пароль?

Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

4.2. Элементы гидростатики

4.2.5. Сообщающиеся сосуды

Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.

Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:

h 1 h 2 = ρ 2 ρ 1 ,

где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.

Указанный закон справедлив в отсутствие сил поверхностного натяжения.

Если сообщающиеся сосуды заполнены однородной жидкостью

ρ1 = ρ2,

то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):

h1 = h2,

где h1 – высота столба жидкости в левом колене; h2 – высота столба жидкости в правом колене сообщающихся сосудов.

Рис. 4.14

Если сообщающиеся сосуды заполнены разнородными жидкостями

ρ1 ≠ ρ2,

то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение

h 1 h 2 = ρ 2 ρ 1 ,

где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.

Рис. 4.15

Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой

p1 = ρ1gh1,

в правом колене –

p2 = ρ2gh2 + ρ3gh3.

Рис. 4.16

Равенство давлений на указанном уровне

p1 = p2

позволяет записать тождество:

ρ1h1 = ρ2h2 + ρ3h3.

Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.

Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.

Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:

• в первом сосуде оказывается масса жидкости

m1 = ρV1 = ρ∆h1S1,

где ρ – плотность жидкости; V1 = S1∆h1 – объем жидкости в первом сосуде; S1 – площадь поперечного сечения первого сосуда; ∆h1 – повышение уровня жидкости в первом сосуде;

• во втором сосуде оказывается масса жидкости

m2 = ρV2 = ρ∆h2S2,

где V2 = S2∆h2 – объем жидкости во втором сосуде; S2 – площадь поперечного сечения второго сосуда; ∆h2 – повышение уровня жидкости во втором сосуде.

Повышение уровней жидкости в обоих сосудах одинаково:

∆h1 = ∆h2 = ∆h,

поэтому масса жидкости, добавленной в систему, определяется формулой

m = m1 + m2 = ρ∆h(S1 + S2).

Выразим отсюда искомое значение ∆h:

Δ h = m ρ ( S 1 + S 2 ) .

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для первого (широкого) сосуда

S 1 = π d 1 2 4 ,

• для второго (узкого) сосуда

S 2 = π d 2 2 4 ,

где d1 = 2d2 – диаметр первого (широкого) сосуда; d2 – диаметр второго (узкого) сосуда.

Отношение площадей

S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4

позволяет найти площадь широкого сосуда:

S1 = 4S2.

Подставив S1 в формулу для ∆h

Δ h = m ρ ( 4 S 2 + S 2 ) = m 5 ρ S 2 ,

рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:

Δ h = 0,12 5 ⋅ 1,6 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 15 ⋅ 10 − 3 м = 15 мм.

Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем – 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.

Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:

p1 = p2,

где p1 – давление в широком сосуде; p2 – давление в узком сосуде.

На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.

Гидростатическое давление на выбранном уровне:

• в широком сосуде

p1 = ρ1gh1,

где ρ1 – плотность жидкости, заполняющей систему изначально; g – модуль ускорения свободного падения; h1 – высота столба жидкости в широком сосуде;

• в узком сосуде

p2 = ρ2gh2 + ρ3gh3,

где ρ2 – плотность первой жидкости, добавленной в узкий сосуд; h2 – высота столба первой жидкости; ρ3 – плотность второй жидкости, добавленной в узкий сосуд; h3 – высота столба второй жидкости.

Равенство давлений на указанном уровне

ρ1gh1 = ρ2gh2 + ρ3gh3

позволяет определить высоту столба жидкости в широком сосуде:

h 1 = 1 ρ 1 ( ρ 2 h 2 + ρ 3 h 3 ) ,

где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:

• для первой жидкости

h 2 = m 2 ρ 2 S 2 ;

• для второй жидкости

h 3 = m 3 ρ 3 S 2 ,

где S2 – площадь поперечного сечения узкого сосуда; m2 – масса первой жидкости, добавленной в узкий сосуд; m3 – масса второй жидкости, добавленной в узкий сосуд.

Подстановка h2 и h3 в формулу для h1 дает

h 1 = 1 ρ 1 ( ρ 2 m 2 ρ 2 S 2 + ρ 3 m 3 ρ 3 S 2 ) = m 2 + m 3 ρ 1 S 2 .

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для широкого сосуда

S 1 = π d 1 2 4 ,

• для узкого сосуда

S 2 = π d 2 2 4 ,

где d1 = 2d2 – диаметр широкого сосуда; d2 – диаметр узкого сосуда.

Отношение площадей

S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4

позволяет найти площадь узкого сосуда:

S 2 = S 1 4 .

Таким образом, высота столба жидкости в широком сосуде определяется выражением

h 1 = 4 ( m 2 + m 3 ) ρ 1 S 1 .

Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:

h 2 + h 3 = m 2 ρ 2 S 2 + m 3 ρ 3 S 2 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) .

Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле

Δ h = ( h 2 + h 3 ) − h 1 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) − 4 ( m 2 + m 3 ) ρ 1 S 1 =

= 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 − ( m 2 + m 3 ) ρ 1 ) .

Произведем вычисление:

Δ h = 4 10 ⋅ 10 − 4 ( 0,12 2,0 ⋅ 10 3 + 0,12 4,0 ⋅ 10 3 − 0,12 + 0,12 6,0 ⋅ 10 3 ) = 0,20 м = 20 см.

Источник

Определение

Соединенные между собой сосуды называют сообщающимися.

В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.

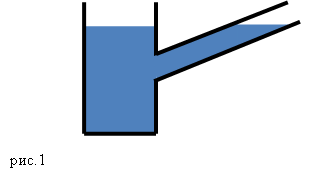
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:

[p=rho gh left(1right),]

где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.

Жидкости разной плотности в сообщающихся сосудах

Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).

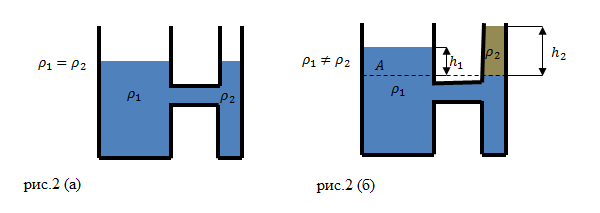
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:

[{rho }_1gh_1={rho }_2gh_2left(2right),]

где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:

[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]

Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.

Гидравлический пресс и другие примеры использования сообщающихся сосудов

В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.

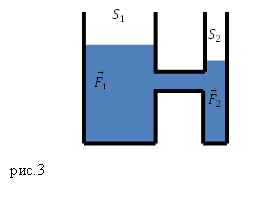
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:

[p_1=frac{F_1}{S_1}left(4right).]

Второй поршень давит на жидкость:

[p_2=frac{F_2}{S_2}left(5right).]

Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:

[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]

Получим:

[F_1=F_2frac{S_1}{S_2}(7)]

величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.

По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.

Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.

Примеры задач с решением

Пример 1

Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.

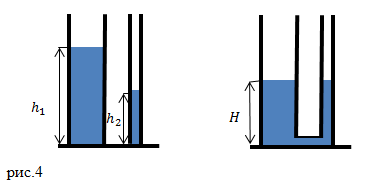
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:

[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]

где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:

[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]

где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:

[Delta V_1=Delta V_2left(1.3right).]

Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:

[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]

Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:

[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=] [=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]

Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$

Пример 2

Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?

Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):

[F_1=F_2frac{S_1}{S_2}(2.1)]

Ответ. $F_1=F_2frac{S_1}{S_2}$

Читать дальше: условия плавания тел.

Источник