Как найти массу тела сосуда с водой

Предположим на дне водоема находится некий объект, который нам необходимо поднять на поверхность. Для расчета толщины металлического троса необходимо знать массу этого объекта. Как можно измерить массу объекта находящегося на дне водоема? bezdelnik 4 года назад Измерить массу тела находящегося на дне водоёма нельзя, её можно только рассчитать. Для этого надо опустить на дно водолаза или батискаф,определить форму тела и произвести измерения его размеров, отрезать небольшой кусок тела, поднять его на поверхность и определить его плотность ρ в кг/дм3, подсчитать, исходя из размеров и формы, объём тела V в дм3. Тогда массу тела m можно рассчитать по формуле m=ρ*V кг. автор вопроса выбрал этот ответ лучшим Sachishin 4 года назад Массу можно найти по закону Архимеда. F=ρgV. V- объём вытесняемой жидкости,ρ – ее плотность. откуда находим массу вытесненной жидкости m=ρV. А массы вытесненной жидкости будет равна массе тела,погруженного в жидкость RIOLIt 4 года назад Так не бывает,- в воду падают известные предметы,- автомобиль, так его масса известна, труба- семисотка валяется, тоже- “не бином Ньютона”,( и так далее, и тому подобное…) Грустный Роджер 4 года назад Масса тела не зависит от того, погружено оно в воду или нет. От этого зависит вес. Поэтому для измерения массы надо просто вынуть тело из воды, высушить его и воспользоваться любыми подходящими весами. Лучше рычажными, а не пружинными. Magnus 4 года назад Если бы знать, какой конкретно объект вам нужно поднять, можно было бы предложить что-то конкретное, а так… Масса тела, погруженная в воду, равняется произведению его объема на (плотность минус единица). Знаете ответ? |
Источник
Задачи на плотность, массу и объем с решением
Формулы, используемые в задачах по физике на плотность, массу и объем.
Название величины | Обозначение | Единицы измерения | Формула |
Масса | m | кг | m = p * V |
Объем | V | м3 | V = m / p |
Плотность | p | кг/м3 | p = m / V |
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Найдите плотность молока, если 206 г молока занимают объем 200 см3?

Задача № 2.
Определите объем кирпича, если его масса 5 кг?

Задача № 3.
Определите массу стальной детали объёмом 120 см3
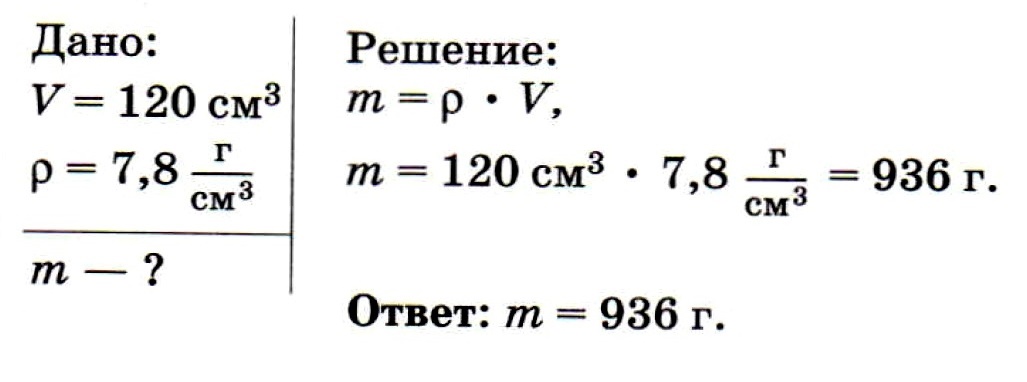
Задача № 4.
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5.
Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.

Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6.
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7.
Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.
Задача № 8 (повышенной сложности).
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
РЕШЕНИЕ: Объем кубика VK = а3 = 216 см3. Объем стенок VС можно вычислить, зная массу кубика mК и плотность меди р: VС = mК / р = 91 см3. Следовательно, объем полости VП = VK — VC = 125 см3. Поскольку 125 см3 = (5 см)3, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.
Задача № 9 (олимпиадный уровень).
Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.
Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?
- Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
- Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
- Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
- Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
- Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
- Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
- Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
Конспект урока «Задачи на плотность, массу и объем с решением».
Следующая тема: «Задачи на силу тяжести и вес тела».
Источник
18 июля 2011
Автор
КакПросто!
Воду, как и любую жидкость, не всегда можно взвесить на весах. Но узнать массу воды бывает необходимо как на некоторых производствах, так и в обычных житейских ситуациях, от расчета резервуаров до решения вопроса, какой запас воды вы можете взять с собой в байдарку или резиновую лодку. Для того, чтобы вычислить массу воды или любой жидкости, помещенной в тот или иной объем, прежде всего необходимо знать ее плотность.
Вам понадобится
- Весы
- Мерная посуда
- Линейка, рулетка или любой другой измерительный прибор
- Сосуд для переливания воды
Инструкция
Если вам нужно вычислить массу воды в небольшом сосуде, это можно сделать с помощью самых обычных весов. Взвесьте сначала сосуд вместе с водой. Затем перелейте воду в другую посуду. После этого взвесьте пустой сосуд. Из массы полного сосуда вычтите массу пустого. Это и будет масса содержавшейся в сосуде воды. Таким образом можно определять массу не только жидких, но и сыпучих веществ, если есть возможность их пересыпать в другую посуду. Такой способ иногда еще можно наблюдать в некоторых магазинах, где нет современного оборудования. Продавец сначала взвешивает пустую банку или бутылку, затем заполняет ее сметаной, взвешивает снова, определяет вес сметаны и только после этого рассчитывает ее стоимость.
Для того, чтобы определить массу воды в сосуде, который невозможно взвесить, необходимо знать два параметра — плотность воды (или любой другой жидкости) и объем сосуда. Плотность воды составляет 1 г/мл. Плотность другой жидкости можно найти в специальной таблице, которая обычно бывает в справочниках по химии.
Если нет мерной посуды, в которую можно перелить воду, вычислите объем сосуда, в котором она находится. Объем всегда равен произведению площади основания на высоту, и с сосудами постой формы обычно проблем не возникает. Объем воды в банке будет равен площади круглого основания на высоту, заполненную водой. Умножив плотность ? на объем воды V, вы получите массу воды m: m=?*V.
Обратите внимание
Определить массу можно и зная количество воды и ее молярную массу. Молярная масса воды равна 18, поскольку состоит из молярных масс 2 атомов водорода и 1 атома кислорода. MH2O = 2MH+MO=2·1+16=18 (г/моль). m=n*M, где m – масса воды, n – количество, M – молярная масса.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Источник
Опубликовано ср, 07/17/2019 – 14:49 пользователем fizportal.ru
ГИДРОСТАТИКА. Вес тела. Сила Архимеда. Тема 12-2
12.18. Вес тела в воде в 2 раза меньше, чем в воздухе. Какова плотность вещества тела? Ответ дайте в г/см3.
12.19. Решите задачу Архимеда – найдите массу золота (в г) в короне, изготовленной из сплава золота с серебром. Вес короны в воздухе 25,4 H, в воде – 23,4 H. Плотность золота 19,3 г/м3, серебра – 10,5 г/м3.
12.20. Самородок золота вместе с кварцем, в который он заключен, растягивает пружину динамометра с силой 2,26 Н. При погружении самородка в воду на него действует выталкивающая сила 0,2 Н. Найдите массу (в г) самородка золота. Плотность золота 19,3 г/см3, кварца – 3,3 г/см3.
12.21. В цилиндрический сосуд с площадью дна 100 см2 налита вода. На какую величину изменится давление на дно сосуда, если на поверхности воды будет плавать кусок льда массой 300 г?
12.22. Полый шар плавает в жидкости, наполовину погрузившись в нее. Какую долю объема шара (в процентах) составляет его внутренняя полость? Плотность жидкости в 2 раза меньше плотности вещества шара.
12.23. Тело плавает на границе двух жидкостей. Плотность тяжелой жидкости в 2,5 раза больше плотности тела, а плотность легкой – в 2 раза меньше плотности тела. Какая часть объема тела (в процентах) погружена в тяжелую жидкость?
12.24. Определите выталкивающую силу (в кН), действующую на погруженный в воду камень объемом 0,5 м3.
12.25. Чему равна архимедова сила (в мН), действующая в воздухе на тело объемом 50 дм3? Плотность воздуха 1,29 кг/м3.
12.26. Какую силу надо приложить, чтобы удержать в воде камень, вес которого в воздухе 350 Н? Плотность вещества камня 2500 кг/м3.
12.26. Кусок алюминия в воздухе весит 270 Н, а в глицерине 144 Н. Определите плотность глицерина, если плотность алюминия равна 2700 кг/м3.
12.27. На какую величину плотность некоторого тела больше, чем у жидкости с плотностью 800 кг/м3, если вес тела в этой жидкости в 3 раза меньше, чем в воздухе?
12.28. Плотность некоторого тела в 1,25 раза больше, чем плотность воды. Во сколько раз вес этого тела в воде будет меньше, чем в воздухе?
12.29. Кусок металла весит в воде 6800 Н, а в бензине 7100 Н. Определите плотность бензина. Плотность металла 7800 кг/м3.
12.30. Тело весит в воздухе 3 Н, в воде 1,8 Н и в жидкости неизвестной плотности 2,04 Н. Какова плотность этой неизвестной жидкости?
12.31. Кусок пробки имеет в воздухе вес 1 Н, кусок некоторого металла 10 Н. Если эти куски связать ниткой и погрузить полностью в керосин, то их общий вес будет 5 H. Найдите плотность пробки. Плотность керосина 800 кг/м3, металла – 4000 кг/м3.
12.32. В цилиндрический сосуд радиусом R налита вода. На сколько повысится уровень воды, если в сосуд поместить деревянный брусок массой M?
12.33. Кубик со стороной 5 см плавает между керосином и водой, находясь ниже уровня керосина на 2,5 см. Нижняя поверхность кубика на 1 см ниже поверхности раздела. Какова плотность кубика? Изменится ли глубина погружения в воду при доливании керосина?
12.34. В сосуде с водой плавает кусок льда. Что будет с уровнем воды в сосуде после того, как лед растает? Что будет, если в сосуд вместо воды налить жидкость с большей плотностью?
12.35. Полый шар из чугуна (7800 кг/м3) плавает в воде, погрузившись в нее ровно наполовину. Найти объем внутренней полости шара. Масса шара 3,9 кг.
12.36. В цилиндрическом сосуде с несмешивающейся с водой жидкостью, плотность которой r = 1,2 г/см3, при температуре t = 0 оС плавает льдинка массой m = 1 кг. На какую величину изменится уровень этой жидкости в сосуде, когда льдинка растает? Площадь основания сосуда S = 10–1 м2.
12.37. В одном из двух одинаковых заполненных водой цилиндрических сообщающихся сосудов плавает шарик. Масса шарика m, плотность воды $rho$, сечение каждого сосуда (площадь дна) S. На сколько изменится уровень воды, если вынуть шарик?
Ответ
Источник
Учимся решать экспериментальные задачи: учащимся 7-10 класса, желающим участвовать в олимпиадах по физике
Физика – наука экспериментальная. Именно поэтому проведение экспериментального тура уже давно вошло в практику физических олимпиад. Выполняя задания этого тура, учащиеся должны продемонстрировать умение своими руками создать экспериментальную установку, провести на ней измерения, выявить определенные физические закономерности, оценить точность полученных результатов.
Решение экспериментальных задач воспитывает стремление собственными силами добывать знания, активно познавать Мир, приучает самостоятельно анализировать явления, заставляет напряженно думать, привлекая свои теоретические знания и практические навыки. Разбор экспериментальных задач воспитывает критический подход к результатам измерений, привычку обращать внимание на условия, при которых производится эксперимент. Экспериментальные задачи помогают лучше решать расчетные, так как при решении экспериментальных задач ученику приходится сначала осмыслить физическое явление или закономерность, выявить, какие данные ему нужны, продумать способы и возможности их определения, найти их и только на заключительном этапе уже вполне осмысленно подставить в формулу.
Предлагаем несколько экспериментальных задач с решением по теме «Законы гидростатики» из числа тех, что предлагались в разное время на олимпиадах по физике самого разного уровня: от городского до российского.
Экспериментальные задачи
Задача 1. Определите плотность деревянного бруска.
Оборудование: линейка, сосуд с водой, мерный стакан.
Указание. Воспользуйтесь условием плавания тела: если тело плавает, значит, сила тяжести равна выталкивающей силе.
Возможное решение. Заполним сосуд (рекомендуется взять пластиковую тарелку) водой насколько это возможно. Пусть объем жидкости равен Vтaр. Аккуратно опустим брусок в пластиковую тарелку с водой. Объем вытесненной воды V1 определим с помощью мерного стакана. Аккуратно погрузим весь брусок в воду. Некоторая часть воды вновь выльется из тарелки. Ясно, что всего из тарелки будет вытеснен объем воды равный объему бруска Vбрус. ρвV1= Vбрусρбрус Þ ρбрус = ρвV1/Vбрус. Несмотря на идейную простоту, задача требует известного экспериментального искусства и внимательности: объем воды умещающийся в тарелке оказывается больше объема тарелки, т. к. заметная часть воды “возвышается” над краем тарелки за счет сил поверхностного натяжения. Небрежно выполненный эксперимент приводит к ощутимой ошибке в определении плотности дерева.
Задача 2. Определите плотность металла, находящегося в одном из двух кусков пластилина, если известно, что массы пластилина в обоих кусках одинаковы. Оцените точность полученного результата. Извлекать металл из пластилина не разрешается.
Оборудование: весы с разновесами, стакан с водой, штатив, два одинаковых по массе куска пластилина, небольшой кусок металла или моток проволоки, введенный внутрь одного из кусков пластилина.
Возможное решение. Задача очень похожа на знаменитую задачу о короне царя Гиерона (определение наличия примесей в золоте), только с более доступными материалами — пластилином и железом (кусок железа находился внутри пластилина).
Пользуясь весами с разновесами, можно определить массу куска пластилина с металлом (mпл+mм), массу чистого пластилина mпл и по их разности — массу металла mм, находящегося в одном из кусков пластилина. Взвесив данные куски пластилина сначала в воздухе, а потом в воде, можно найти выталкивающую силу и, зная плотноcть воды, можно вычислить объемы кусков (Vпл+Vм) и Vпл. Объем металла Vм можно определить по разности этих объемов.
Тогда плотность металла ρм= mм/Vм.
Возможны два варианта: в одних кусках пластилинa находился кусок алюминия, в других – кусок железа.
Весьма интересным было бы решение этой задачи, если бы вместо определенного куска чистого пластилина массой, равной массе пластилина в составном куске, давался просто пластилин (в неопределенном количестве). В этом случае для решения задачи надо было бы взять кусок чистого пластилина, масса которого равна массе (m) составного куска (объема V), и определить его объем V0. Плотность металла можно найти, решив следующую систему четырех уравнений с четырьмя неизвестными:
m = ρмVм+ ρплVпл
V = Vпл+Vм
V0 = Vпл+Vм
ρпл= m/ V0
Задача 3. Определите плотность тела.
Оборудование: динамометр, стакан с водой, стакан с машинным маслом, тело неправильной формы.
Возможное решение. На тело, подвешенное на нити в жидкости, действуют три силы: сила тяжести F1 = mg, архимедова сила FA и сила натяжения нити Т (рис.5).
Модуль силы натяжения равен весу тела в жидкости: ‘Г – Р. Направим координатную ось OY вертикально вверх и запишем условие равновесия тела и проекциях на эту ось: Т+ FA- Fт= 0.
Отсюда T = Fт – FA, или T = mg – ρжgV = g(m – ρжV).
Таким образом, получаем следующую формулу для веса тела массой m в жидкости с плотностью ρж: Р= g(m – ρжV).
Для двух разных жидкостей имеем:
P1= g(m – ρ1V);
P2 = g(m – ρ2V).
Разделив левые и правые части этих уравнений на gV и учтя, что ρ =, получим: = ρ – ρ1; = ρ – ρ2. Решая совместно эти уравнения, найдем плотность тела ρ = . Измерив вес тела в двух разных жидкостях с известными плотностями, рассчитаем плотность твердого тела.
Задача 4. Определите плотность неизвестной жидкости.
Оборудование: динамометр, стакан с водой, стакан с неизвестной жидкостью, грузик.
Возможное решение. Определим вес тела в двух различных жидкостях Р1 и Р2. Вес тела в жидкости равен: P1= mg – FA1 = mg – ρ1gV;
P2 = mg – FA2 = mg – ρ2gV или
mg – P1 = ρ1gV;
mg – P2 = ρ2gV.
Отсюда =; ρ2 = ρ1.
Задача 5. Найдите плотность деревянного бруска и кусочков металла.
Оборудование: мерный сосуд, деревянный брусок, мелкие кусочки металла, сосуд с водой.
Возможное решение. Пусть V0- объем воды, налитой в мерный сосуд. Опустим брусок плавать. При этом суммарный объем воды и погруженной в воду части бруска (измеренный по шкале сосуда) обозначим через V1.
Будем накладывать на брусок кусочки металла до тех нор, пока его верхняя грань не окажется на одном уровне с поверхностью воды. Новый суммарный объем воды и погруженного в воду бруска обозначим V2. Сбросим теперь кусочки металла в сосуд. Суммарный объем воды и бруска обозначим V3. Запишем условие равновесия для обеих ситуаций, когда брусок погружен в воду полностью, а кусочки металла находятся на нем, и когда кусочки металла сброшены с бруска в воду: ρбVбg = ρвgVп; ρмVмg+ ρ бVбg = ρвgVб, где ρб – плотность бруска, Vб – его объем, Vп – объем погруженной части бруска, ρм – плотность металла, Vм – суммарный объем всех кусочков металла.
ρб = ; ρм = ; => ρб = ; ρм =.
Задача 6. Определить плотность данной жидкости.
Оборудование: сосуд с неизвестной жидкостью, сосуд с водой, измерительная линейка, два металлических бруска, рычаг.
Примечание. Плотность воды принять равной 103 кг/м3.
Возможное решение. Надо провести три измерения по установлению равновесия рычага, когда один брусок находится попеременно в воздухе, в воде, в неизвестной жидкости, а другой брусок — все время в воздухе. При этом разумно длину плеча рычага с первым грузом оставлять неизменной, а длину плеча рычага со вторым грузом соответственно изменять. Запишем уравнения моментов сил для трех случаев равновесия рычага (рис.6): m1gl = m2gl1,
(m1g – ρвVg) l= m2gl2, (m1g – ρVg)l = m2gl3.
Исключая из этих уравнений m1, m2, V и g, получаем формулу для определения плотности ρ неизвестной жидкости (раствора медного купороса) : .
Задача 7. Определить плотность неизвестной жидкости (чуть подкрашенный концентрированный раствор поваренной соли в воде).
Оборудование: небольшая колба известного объема с тонким длинным горлышком и миллиметровка. Неизвестная жидкость налита в один большой сосуд, обычная вода — в другой.
Возможное решение. Один из способов измерения: сделать из колбочки ареометр, налив туда некоторое количество жидкости и пустив ее плавать в сосуде с водой. Количество жидкости нужно подобрать так, чтобы над поверхностью торчало только горлышко колбы, диаметр которого легко измерить,— в этом случае можно произвести теоретический расчет плотности. Для достижения приемлемой точности приходится учитывать и поверхностные эффекты. В целом задача не очень сложная, но требует аккуратности в измерениях.
Задача 8. Взвешивание сверхлёгких грузов. Определить с помощью предложенного оборудования массу m кусочка фольги.
Оборудование. Банка с водой, кусок пенопласта, набор гвоздей, деревянные зубочистки, линейка с миллиметровыми делениями, остро отточенный карандаш, фольга, салфетки.
Возможное решение. Измеряем диаметр d цилиндрической части зубочистки методом рядов (положив несколько зубочисток плотно в ряд и измерив линейкой их общую ширину). На одну из зубочисток наносим карандашом через 1 мм деления.
Втыкаем в пенопласт гвоздики, пока он не погрузится в воду почти полностью. Сверху втыкаем зубочистку с делениями, чтобы пенопласт был ниже уровня воды, а зубочистка вертикально выступала из воды не меньше, чем на 3/4 длины. При необходимости от пенопласта можно отделить небольшой кусо чек. Затем на верхний конец зубочистки прикрепляем кусочек фольги (рис.7) и находим изменение Δh глубины погружения зубочистки.
Изменение объёма ΔV погруженной части: ΔV=, откуда масса фольги m=ρΔV=ρΔhd2, где ρ — плотность воды.
Рекомендации для организаторов. Для эксперимента подходит литровая банка (или двухлитровая пластиковая бутылка с отрезанным верхом), она должна быть наполнена водой почти до краёв. Зубочистки должны быть не искривлёнными, одинакового диаметра, а их длина должна быть не меньше 6 см, количество: 5 ¸ 10 штук. Размеры пенопласта: высота 0,5 ¸ 1 см, длина и ширина 2 ¸ 4 см. Размеры фольги должны быть такими, чтобы под её весом зубочистка погружалась приблизительно на 2/3 своей длины. Для пищевой фольги эти размеры составляют от 2 см х 2 см до 4 см х 4 см. Масса гвоздей должна позволять утопить пенопласт. Гвозди следует взять разного диаметра: крупные — для грубой настройки системы, а мелкие — для точной.
Задача 9. Определите массу тела.
Оборудование: пружина, тело неизвестной массы, мензурка, штатив с муфтой и лапкой, сосуд с водой, линейка измерительная.
Возможное решение. Подвесим к пружине груз неизвестной массы и измерим удлинение х, пружины. Условие равновесия груза на пружине в воздухе запишем так:
mg = kx1 (1).
Опустим груз в сосуд с водой и измерим новое удлинение х2 пружины. Условие равновесия для груза, опушенного в сосуд с водой: mg – FA = kx2 (2), где FA – архимедова сила, действующая на груз. Она равна FA = p0gV, где ρ0 – плотность воды, V – объем тела.
Измерив объем тела с помощью мензурки, используя выражения (I) и (2), рассчитаем жесткость пружины: k = и искомую массу груза: m = .
Контрольное задание по физике №3 для учащихся 7-10 классов.
Задача 10. Определите плотность растительного масла.
Оборудование: линейка, сосуд с водой, сосуд с маслом.
Указание: Плотность неизвестной жидкости (в данном случае, масла) можно определить методом сравнения масс при равных объемах или методом сравнения объемов при равных массах. Считайте плотность воды известной, равной 1000 кг/м3. Воспользуйтесь линейкой как рычагом.
Задача 11. Определить плотность дерева, из которого изготовлена палочка.
Оборудование: линейка, деревянная палочка, узкий цилиндрический сосуд с водой.
Задача 12. Определите плотность стекла, из которого изготовлена банка из-под майонеза.
Оборудование: майонезная банка, мензурка объемом V=250 мм3, стеклянный сосуд, полоска из мягкого металла размером 2х20 см, сосуд с водой (водопроводный кран).
Источник
