Как найти массу воздуха в сосуде
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Воздушный шар, оболочка которого имеет массу (M) = 145 кг и объём (V) = 230 м(^3), наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры (t) = 265 (^{circ})С. Определите максимальную температуру (t_o) окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок).
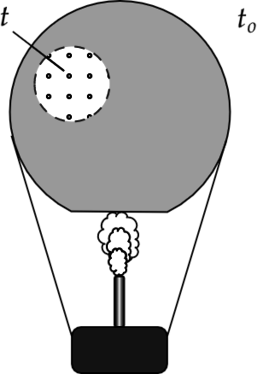
“Демоверсия 2019”
Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):
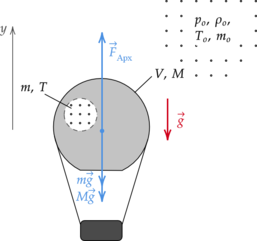
Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} – mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V – m – M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o – m – M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} – dfrac{p_o VMr}{RT} – M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} – dfrac{1}{T} – dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]
Ответ: 0 ∘С (273 К)
В теплоизолированном сосуде в начальный момент находится одноатомный газ при температуре (T_o) = 300 К и кусочек железа массой (m) = 2 кг, нагретый до температуры (T_1) = 500 К. Начальное давление газа (p_o) = 10(^5) Па, его объем (V_o) = 10000 см(^3), удельная теплоемкость железа (c) = 0,45 кДж/(кг(cdot)К). Найдите давление газа в равновесном состоянии, считая объем газа неизменным.
Так как по условию задачи система замкнута, то внутренняя энергия ее неизменна. Поэтому равновесное состояние системы будет устанавливаться при передаче тепла газу от более горячего куска железа. По первому закону термодинамики: [Delta U=Q-A,] где (Delta U) — изменение внутренней энергии, (Q) — количество теплоты, которое подводили к телу, (A) — работа газа.
В данном случае работа газа равна нулю, так как (V=const). Уравнение теплового баланса в этом случае имеет вид: [dfrac{3}{2}nu R(T-T_o)=cm(T_1-T), hspace{7 mm} (1)] где (nu) — количество вещества газа, (R) — универсальная газовая постоянная.
Запишем уравнение Менделеева – Клапейрона: [p_oV_o=nu R T_o] Выразим отсюда: [hspace{5 mm} nu R=dfrac{p_oV_o}{T_o} hspace{7 mm} (2)] Выразим из (1) температуру газа (T): [T=dfrac{cmT_1+1,5nu RT_0}{cm+1,5nu R}hspace{5 mm} (3)] Так как объем постоянен и количество вещества газа не меняется, то по закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_o}{T_o}hspace{3 mm} Rightarrow hspace{3 mm} p_1=p_ocdotdfrac{T}{T_o}hspace{5 mm} (4)] Подставим (3) в (4): [p_1=p_ocdotdfrac{cmT_1+1,5nu RT_o}{T_o(cm+1,5nu R)}hspace{5 mm} (5)] Подставим (2) в (5): [p_1=p_ocdotdfrac{cmT_1+1,5dfrac{p_oV_o}{T_o}T_o}{T_oleft(cm+1,5dfrac{p_oV_o}{T_o}right)} = p_ocdotdfrac{cmT_1+1,5p_oV_o}{T_ocm+1,5p_oV_o}] Найдем давление газа в равновесном состоянии: [p_1 = 10^5 text{ Па}cdotdfrac{450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг} cdot500 text{ К}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}}{300text{ К}cdot450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}} approx 166 text{ кПа}]
Ответ: 166 кПа
Два литра жидкого аргона находится при температуре своего кипения -186 (^{circ})С. Какое количество теплоты нужно сообщить этому количеству аргона для того, чтобы при постоянном давлении перевести его в газ, имеющий температуру 0 (^{circ})С? Плотность жидкого аргона 1400 кг/м(^3), его удельная теплота испарения 87 кДж/кг.
Чтобы перевести аргон в газ, имеющий температуру 0 (^circ)С, сначала необходимо перевести его из жидкого состояния в газообразное, а затем нагреть до нужной температуры.
Общее количество теплоты (Q), которое необходимо для этого, будет складываться из двух составяющих: [; ; ; ; Q = Q_1 + Q_2 ; ; ; ; (1)] Количество теплоты, которое потребуется для парообразования аргона: [; ; ; ; Q_1=rm, ; ; ; ; (2)] где (m) — масса аргона, (r) — удельная теплота испарения.
Когда аргон превратится в газ, мы будем его рассматривать как идеальный одноатомный газ. Значит, для нагрева аргона до 0 (^{circ}) С запишем перове начало термодинамики: [Q_2=Delta U+A,] где (Q_2) — количество теплоты, необходимое для нагревания, (Delta U) — изменение внутренней энергии аргона, (A) — работа аргона.
[Q_2=dfrac{3}{2}nu RDelta T+p(V_2-V_1), hspace{7 mm} (3)] где (nu) — количество вещества, (Delta T) — изменение температуры, (p) — давление, (V_2) и (V_1) — конечное и начальное давлени газа, а в дальнейшнем (mu) — молярная масса газа, (rho) — плотность аргона.
По уравнению Клапейрона — Менделеева: [p(V_2-V_1)=nu R Delta T hspace{7 mm} (4)] Подставим (4) в (3): [Q_2=dfrac{3}{2}nu RDelta T+nu RDelta T] [; ; ; ; Q_2 = dfrac{5}{2}nu RDelta T ; ; ; ; (5)] Подставим (2), (5) в (1): [Q=rm+dfrac{5}{2}nu RDelta T] Количество вещества аргона можно найти по формуле: (nu = dfrac{m}{mu}), где (mu) — молярная масса аргона.
Массу аргона можно найти, зная его плотность и объем: (m = rho V).
С учетом этого: [Q=rrho V+dfrac{5}{2}cdotdfrac{rho V}{mu}RDelta T] [Q=87cdot10^3text{ кДж/кг}cdot2cdot10^{-3}text{ м$^3$}cdot1400text{ кг/м$^3$} +dfrac{5}{2}cdotdfrac{1400text{ кг/м$^3$}cdot2cdot10^{-3}text{ м$^3$}}{40cdot10^{-3}text{кг/моль}}cdot8,31cdot186^circtext{C} approx 591 text{ кДж}]
Ответ: 591 кДж
Когда легковой автомобиль едет с постоянной скоростью по горизонтальному шоссе, расход бензина составляет (mu_1) = 7 л/100 км. Каков будет расход бензина (mu_2), если этот автомобиль поедет с той же скоростью вверх по наклонному участку шоссе, образующему угол (alpha) = 0,01 рад с горизонтом? Качество дорожного покрытия на горизонтальном и наклонном участках шоссе одинаково. Масса автомобиля (M) = 1000 кг, коэффициент полезного действия двигателя (eta = 30%), удельная теплота сгорания бензина (q) = 42 МДж/кг, плотность бензина (rho) = 0,7 кг/л. При расчетах положить (sin alpha approx alpha).
По условию задачи КПД двигателя автомобиля равен 30%. Это означает, что только 30% от выделевшегося количества теплоты пойдет на совершение работы по перемещению автомомбиля: [; ; ; ; A = 0,3Q ; ; ; ; (1)] Количество теплоты, которое выделится при сгорании бензина, равно: [; ; ; ;Q = qm ; ; ; ; (2)] где (m) — масса сгоревшего бензина.
Массу бензина можно найти, зная его плотность: [; ; ; ; rho = dfrac{m}{V} ; ; ; Rightarrow ; ; ; m = rho V ; ; ; ; (3)] где (V) — объем сгоревшего бензина.
Зная расход бензина и пройденное расстояние, найдем объем израсходованного бензина: [; ; ; ;V = mu l ; ; ; ;(4)] Подставим последовательно (4), (3), (2) в (1): [; ; ; ;A = 0,3qrhomu l ; ; ; ; (5)] В то же время работа при перемещении автомобиля на расстояние (l) по определению равна: [A = Flcosalpha_o] где (F) — модуль равнодействующей всех сил, действующих на автомобиль, (alpha_o) — угол между направлением силы и направлением перемещения.
В рассматриваемых случаях и для горизонтального движения и для движения под углом к гори3 зонту (cosalpha = 1): [; ; ; ; A = Fl ; ; ; ;(6)] 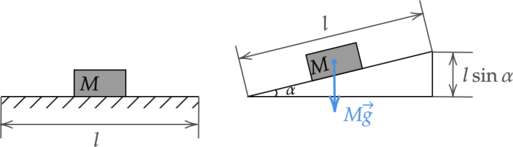
Рассмотрим движение автомобиля по горизонтальному участку шоссе.
В этом случае работа, совершенная двигателем, по величине равна работе сил сопротивления.
Исходя из формул (5) и (6), получаем, что: [0,3qrhomu_1 l = Fl] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_1 ; ; ; ; (7)] Рассмотрим движение автомобиля по наклонному участку шоссе той же длины.
В этом случае работа двигателя равна сумме величины работы сил сопротивления и изменения (приращения) потенциальной энергии автомобиля в поле силы тяжести: [A = Fl + Mglsinalpha] С учетом формулы (5) имеем, что: [0,3qrhomu_2 l = Fl + Mglsinalpha] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_2 – Mgsinalpha ; ; ; ; (8)] Приравняем (7) и (8) с учетом того, что по условию (sinalpha approx alpha), и выразим искомый расход бензина: [0,3qrhomu_1 = 0,3qrhomu_2 – Mgsinalpha] [mu_2 = mu_1 + dfrac{Mgalpha}{0,3rho q}] [mu_2 = 7(text{ л/$100$ км}) + dfrac{1000text{ кг}cdot10text{ м/с}^2cdot0,01}{0,3cdot0,7text{ кг/л}cdot 42cdot10^6text{ Дж/кг}}cdot10^5 approx 8,13text{ л/100 км}]
Ответ: 8,13 л/100 км
Мальчик решил подняться в воздух на воздушных шарах с гелием. Известно, что мальчик весит 40 кг, а на улице нормальное атмосферное давление и температура 27 (^{circ})С. Учитывая, что объем одного шара составляет 10 литров, найдите, сколько потребуется шаров для такого путешествия. Массой оболочки шаров и объемом мальчика пренебречь.
Cила тяжести, действующая на систему, уравновешивается силой Архимеда.
Рассмотрим предельный случай, когда мальчик на воздушных шарах вот-вот оторвется от поверхности земли, и запишем второй закон Ньютона для данной системы: [vec{F}_text{Арх} + Mvec{g} + nmvec{g} = 0] где (M) — масса мальчика, (m) — масса гелия в одном шарике, (n) — количество шаров, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на вертикальную ось, направленную вверх: [F_text{Арх} – Mg – nmg = 0] [; ; ; ; F_text{Арх} = Mg + nmg ; ; ; ; (1)] Сила Архимеда равна: [F_text{Арх} = rho_o gnV] где (rho_o) — плотность воздуха, (V) — объем одного шарика.
Подставим (2) в (1): [rho_o gnV = Mg + nmg] [; ; ; ; rho_o nV = M + nm ; ; ; ; (3)] Запишем уравнение Менделеева-Клапейрона для воздуха: [; ; ; ; p_oV_o = dfrac{m_o}{mu_o} RT_o ; ; ; ; (4)] где (p_o) — атмосферное давление, (V_o) — объем, занимаемый воздухом, (m_o) — (mu_o) — масса воздуха, (R) — универсальная газовая постоянная, (T_o) — абсолютная температура воздуха.
Плотность воздуха равна: [; ; ; ; rho_o = dfrac{m_o}{V_o} ; ; ; ; (5)] Подставим (5) в (4) и выразим плотность воздуха: [; ; ; ; p_o = dfrac{rho_o}{mu_o}RT_o ; ; ; Rightarrow ; ; ; rho_o = dfrac{p_omu_o}{RT_o} ; ; ; ; (6)] Найдем массу гелия в одном шарике из уравнения Менделеева-Клапейрона: [; ; ; ; p_o V = dfrac{m}{mu}RT_o ; ; ; Rightarrow ; ; ; m = dfrac{p_o Vmu}{RT_o} ; ; ; ; (7)] где (m) — масса гелия, (mu) — молярная масса гелия.
Подставим (6), (7) в (3) и выразим количество шариков: [M + ndfrac{p_o Vmu}{RT_o} = dfrac{p_o mu_o}{RT_o}nV] [n = dfrac{MRT_o}{p_o V(mu_o – mu)}] [n = dfrac{40text{ кг}cdot8,31text{Дж/(моль$cdot$К)}cdot300text{ К}}{10^5text{ Па}cdot10^{-2}text{ м}^3cdot(29-4)cdot10^{-3} text{кг/моль}}=3989]
Ответ: 3989
Воздушный шар, оболочка которого имеет массу (M) = 145 кг и объём (V) = 230 м(^3), наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры (t) = 265 (^{circ})С. Определите максимальную температуру (t_o) окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок). 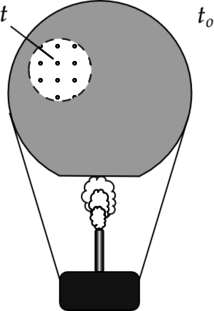
Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):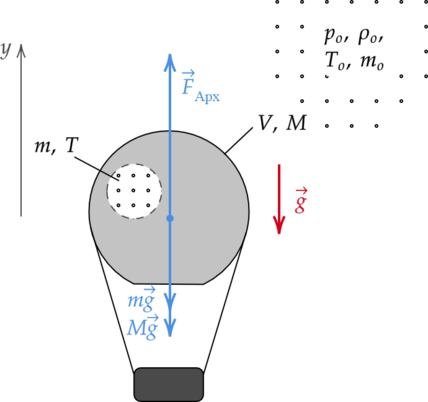
Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} – mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V – m – M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o – m – M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} – dfrac{p_o VMr}{RT} – M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} – dfrac{1}{T} – dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]
Ответ: 0 ∘С (273 К)
Сосуд объемом (V) л, содержащий (nu) моль воздуха при давлении (p) Па и температуре (T_o) К, сверху заткнут пробкой массой (m) кг с площадью (S) см(^2). Найдите на какую величину надо увеличить температуру газа, чтобы пробка вылетела из сосуда, если коэффицент трения пробки о стенки сосуда равен (mu), а атмосферное давление равно (p_o).
Запишем 2 закон Ньютона для предельного случая, когда пробка вот-вот вылетит из сосуда: [; ; ; ; F = F_text{тяж}+F_text{тр}+F_text{атм}, ; ; ; ; ; (1)] где (F) — сила, с которой газ воздействует на пробку, (F_text{тяж}) — сила тяжести, действующая на пробку , (F_text{тр}) — сила трения пробки о стенки сосуда, (F_text{атм}) — сила давления атмосферы на пробку.
Сила, с которой газ воздействует на пробку, равна: [; ; ; ; p=dfrac{F}{S} ; ; ; Rightarrow ; ; ; F=pS ; ; ; ; (2)] По уравнению Клайперона – Менделеева: [; ; ; ; pV=nu R T ; ; ; Rightarrow ; ; ; p=dfrac{nu R T}{V},; ; ; ; (3)] где (T) — абсолютная температура газа, (Delta T) — изменение температуры газа.
Подставим (3) в (2): [; ; ; ; F = dfrac{nu R T}{V}S ; ; ; ; (4)] Сила давления атмосферы на пробку равна: [; ; ; ; F_text{атм}=p_oS ; ; ; ; (5)] Силу тяжести и силу трения найдем по формулам: [; ; ; ; F_text{тяж}=mg ; ; ; (6) ; ; ; ; ; ; ; ; ; ; ; F_text{тр}=mu mg, ; ; ; (7)] где (g) — ускорение свободного падения.
Подставим (4), (5), (6), (7) в (1) и получим: [; ; ; ; S dfrac{nu R T}{V} = mg +mu m g +p_o S ; ; ; ; (8)] Конечная температура газа равна: [; ; ; ; T=T_o + Delta T ; ; ; ; (9)] Подставим (9) в (8) и выразим (Delta T), на которую нужно увеличить температуру газа, чтобы пробка вылетела: [S dfrac{nu R (T_o + Delta T)}{V} = mg +mu m g +p_o S] [Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o]
Ответ: $Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o$
Источник
Примеры решения задач
скачать (258 kb.)
Доступные файлы (1):
- Смотрите также:
- Боровой А.А., Финкельштейн Э.Б., Херувимов А.Н. Законы электромагнетизма (Документ)
- Второв В.Б. Примеры решения задач по ТАУ (Документ)
- Панова Л.И. Вертикальная планировка (примеры задач) (Документ)
- Денисенко Н.В., Корзюк А.Ф. Учебно-методическое пособие. Линейная алгебра и математический анализ + примеры решения типовых задач (Документ)
- Романцева Л.М., Лещинская З.Л., Суханова В.А. Сборник задач и упражнений по общей химии (Документ)
- Гидравлика и гидростатика. Теория и примеры решения типовых задач (Документ)
- Экзаменационные примеры решения задач по экологии на произведение растворимости (ПР) (Документ)
- Фирганг Е.В. Руководство к решению задач по курсу общей физики (Документ)
- Решенные задачи к экзамену и просто пример решения задач (Документ)
- Колистратова Л.Ф. Сборник задач по электромагнетизму (Документ)
- Авсеев Г.М., Алексеенко А.Ф., Гармаш И.Л. Сборник задач по горной электротехнике (Документ)
- Имаев Д.Х., Ковальски З., Яковлев В.Б., Кузьмин Н.Н., Пошехонов Л.Б., Цапко Г.П. Анализ и синтез систем управления (Документ)
n1.doc
1 ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
Параметры состояния тела
Примеры решения задач
1. Давление воздуха по ртутному барометру равно 770 мм при 0° С. Выразить это давление в барах и Па.
Решение
1мм рт. ст. = 133,3 Па, 770 мм рт. ст. =102700 Па = 1,027 бар.
2. Определить абсолютное давление пара в котле, если манометр показывает Р = 1,3 бар, а атмосферное давление по ртутному барометру составляет 680 мм при t = 25° С.
Решение
Показание барометра получено при температуре t = 25° С. Это показание необходимо привести к 0 єС по уравнению (5):
Ро = Рt (1 – 0,000172 t) = 680 · 0,9957 = 677,1 мм рт. ст.
Абсолютное давление пара в котле по формуле (3) равно
Рабс = 130000 + 677,1 * 133,3 = 0,22 МПа.
3. Давление в паровом котле Р = 0,4 бар при барометрическом давлении 725 мм рт. ст.Чему будет равно избыточное давление в котле, если показание барометра повысится до 785 мм рт. ст., а состояние пара в котле останется прежним? Барометрическое давление приведено к 0 °С.
Решение
Абсолютное давление в котле
Рабс = 400000 + 725 * 133,3 = 136642 Па
Избыточное давление при показании барометра 785 мм рт. ст.
Ризб = 136642 – 785 * 133,3 = 32000 Па.
4. Ртутный вакуумметр, присоединенный к сосуду, показывает разрежение 420 мм при температуре ртути в вакуумметре t = 20 °С. Давление атмосферы по ртутному барометру 768 мм при температуре t = 18 °С. Определить абсолютное давление в сосуде.
Решение
Приводим показания вакуумметра и барометра к температуре ртути 0 °С (уравнение 5):
Рвак = 420 (1—0,000172 * 20) = 418,5 мм рт. ст.
Ратм = 768 (1—0,000172 * 18) = 765,6 мм рт. ст.
Абсолютное давление в сосуде по формуле (4)
Рабс = 765,6 – 418,5 = 347,1 мм рт. ст. = 46,3 кПа.
5. Водяной пар перегрет на 45 °С. Чему соответствует этот перегрев по термометру Фаренгейта?
Решение
При переводе разности температур, выраженной градусами шкалы Цельсия, в градусы Фаренгейта и наоборот надо исходить только из цены деления того и другого термометров. Поэтому формула (8) принимает следующий вид:
Следовательно, для нашего случая
Основные газовые законы
Примеры решения задач
6. Какой объем занимает 1 кг азота при температуре 70 °С и давлении 0,2 МПа.
Решение
Из характеристического уравнения для 1 кг газа (16) имеем
7. Во сколько раз объем определенной массы газа при -20 °С меньше, чем при +20°C, если давление в обоих случаях одинаковое?
Решение
При постоянном давлении объем газа изменяется по уравнению (10):
следовательно
8. Определить массу 5 м3 водорода, 5 м3 кислорода и 5 м3 углекислоты при давлении 6 бар и температуре 100 °С.
Решение
Характеристическое уравнение для произвольного количества газа
РV = mRT.
Значение газовой постоянной берем из табл. (приложение А). Получаем
Rн2. = 4124 дж/(кг·град); Rо2 = 259,8 дж/(кг·град);
Rco2 = 188,9 дж/(кг·град).
Следовательно,
Отсюда:
9. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 15 °С. После расходования части кислорода давление понизилось до 7,6 МПа, а температура упала до 10 °С.
Определить массу израсходованного кислорода.
Решение
Из характеристического уравнения (15) имеем
m = P V / R T .
Следовательно, начальная и конечная масса кислорода соответственно равны
Таким образом расход кислорода:
10. Сосуд емкостью 10 м3 заполнен 25 кг углекислого газа. Определить абсолютное давление в сосуде, если температура в нем 27 °С.
Решение
Из характеристического уравнения (15) имеем
11. Определить подъемную силу воздушного шара, наполненного водородом, если объем его равен 1 м3 при давлении 750 мм рт. ст. и температуре 15 °С.
Решение
На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (весов) воздуха и водорода в объеме шара:
,
где g = 9,81 м/сек2 — ускорение силы тяжести на уровне земли.
Значения плотностей воздуха и водорода могут быть определены из уравнения состояния (15) :
Значения газовых постоянных могут быть легко вычислены или взяты из табл. (приложение А): Rвозд = 287 Дж/(кг·град); Rн2 = 4124 Дж/(кг·град). Так как давление водорода и воздуха равно 750 мм рт. ст., то
Следовательно, подъемная сила шара
12. Какова будет плотность окиси углерода при 20 °С и 710 мм рт. ст., если при 0 °С и 760 мм рт. ст. она равна 1,251 кг/м3?
Решение
Согласно уравнению (22)
Следовательно,
Примерырешениязадач1з-нт/д
24.В котельной электрической станции за 20 ч работы сожжены 62 т каменного угля, имеющего теплоту сгорания 28900 кДж/кг. Определить среднюю мощность станции, если в электрическую энергию превращено 18% тепла, полученного при сгорании угля.
Решение
Количество тепла, превращенного в электрическую энергию за 20 ч работы,
Q=62∙1000∙28900∙0,18 = 3,2∙109 кДж.
Эквивалентная ему электрическая энергия или работа
.
Следовательно, средняя электрическая мощность станции
N=89590 / 20 = 4479 кВт.
25. Паросиловая установка мощностью 4200 кВт имеет КПД равный 0,2. Определить часовой расход топлива, если его теплота сгорания равна 25000 кДж/кг.
Решение
По формуле (67) находим выражение для расхода топлива
Часовой расход топлива составит
0,72 ∙ 4200 = 3024 кг/ч.
26. Найти изменение внутренней энергии 1 кг воздуха при изменении его температуры от 300°С до 50°С. Зависимость теплоемкости от температуры принять линейной.
Решение
Изменение внутренней энергии можно определить на основании формулы (53). Рассчитаем среднюю теплоемкость воздуха в данном интервале температур (табл. В.1 приложения):
Следовательно,
Примеры решения задач 2з-н тд
46. 1 кг кислорода при температуре 127°С расширяется до пятикратного объема; температура его при этом падает до 27єС. Определить изменение энтропии. Теплоемкость считать постоянной.
Решение
По уравнению (100)
47. 1 кг воздуха сжимается по адиабате так, что объем его уменьшается в 6 раз, а затем при V = const давление повышается в 1,5 раза. Определить общее изменение энтропии воздуха. Теплоемкость считать постоянной.
Решение
Изменение энтропии воздуха в адиабатном процессе будет равно нулю. Изменение энтропии в изохорном процессе определится по формуле (103):
следовательно
48. 10 м3 воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400°С. Сжатие производится: 1) изохорно, 2) изобарно, 3) адиабатно и 4) политропно с показателем политропы n = 2,2. Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, определить энтропию воздуха в конце каждого процесса.
Решение
Находим массу 10 м3 воздуха при нормальных условиях:
Определяем изменение энтропии в каждом из перечисленных процессов:
1) изохорное сжатие
2) изобарное сжатие
3) адиабатное сжатие
4) политропное сжатие
49. В процессе политропного расширения воздуха температура его уменьшилась от 25°С до – 37°С. Начальное давление воздуха 4 бар, количество его 2 кг. Определить изменение энтропии в этом процессе, если известно, что количество подведенного к воздуху тепла составляет 89,2 кДж.
Решение
Количество тепла, сообщаемого газу в политропном процессе на основании уравнения (85) составляет
Подставляя значения известных величин, получаем
Отсюда показатель политропы n = 1,2.
Из соотношения параметров политропного процесса определяем конечное давление:
Изменение энтропии по уравнению (101)
50. В сосуде объемом 300 л заключен воздух при давлении 50 бар и температуре 20°С. Параметры среды: Р = 1 бар, t = 20°С. Определить максимальную полезную работу, которую может произвести сжатый воздух, находящийся в сосуде.
Решение
Так как температура воздуха в начальном состоянии равна температуре среды, то максимальная работа, которую может выполнить воздух, может быть получена лишь при условии изотермического расширения воздуха от начального давления Р1= 50 бар до давления среды Р2= 1 бар. Максимальная полезная работа определяется на основании формулы (109):
Lmax(полезн) = T∙ (s2 — s1) – Р ∙ (V2 – V1)
или
Lmax(полезн) = m∙Т ∙ (s2 — s1) — P ∙ (V2 – V1).
Определяем массу воздуха, находящегося в сосуде, и объем воздуха после изотермического расширения:
.
Так как изменение энтропии в изотермическом процессе определяется по формуле (106)
то
51. Определить максимальную полезную работу, которая может быть произведена 1 кг кислорода, если его начальное состояние характеризуется параметрами t1 = 400°С и Р1 = 1 бар, а состояние среды — параметрами t = 20єС,Р = 1 бар.
Решение
Максимальная работа, которую произведет при данных условиях кислород, может быть получена лишь при условии перехода его от начального состояния к состоянию среды обратимым путем. Так как температура кислорода в начальном состоянии выше температуры среды, то прежде всего необходимо обратимым процессом снизить температуру кислорода до температуры среды. Таким процессом может явиться только адиабатное расширение кислорода. При этом конечный объем и конечное давление определяются из следующих соотношений:
;
После адиабатного расширения необходимо обратимым путем при t = const сжать кислород от давления 0,0542 бар до давления окружающей среды, т. е. осуществить изотермическое сжатие кислорода до 1 бар. При этом конечный объем кислорода
Максимальная полезная работа определяется по формуле (110):
Задача может быть решена также и графическим способом –через площади на PV-диаграмме.
Круговыепроцессы
Примеры решения задач
52. 1 кг воздуха совершает цикл Карно (см. рис. 2) в пределах температур t1 = 627°С и t2 = 27oС, причем наивысшее давление составляет 60 бар,а наинизшее — 1 бар.
Определить параметры состояния воздуха в характерныхточках цикла, работу, термический КПД цикла и количество подведенного и отведенного тепла.
Решение
Точка 1: Р1 = 60 бар; Т1 = 900 К. Удельный объем газа определяем из характеристического уравнения (16)
Точка 2: Т2 = 900 К. Давление находим из уравнения адиабаты (процесс 2-3)
Удельный объем находим из уравнения изотермы (процесс 1-2)
Точка 3: Р3 = 1 бар; Т3 = 300 К;
Точка 4: Т4 = 300 К. Давление воздуха находим из уравнения адиабаты (процесс 4 – 1), удельный объем – из уравнения изотермы (процесс 3 – 4):
Термический КПД цикла
Подведенное количество тепла
Отведенное количество тепла
Работа цикла
Для проверки можно воспользоваться формулой (111):
53. Для идеального цикла поршневого ДВС с подводом тепла при V = const определить параметры в характерных точках, полученную работу, термический КПД, количество подведенного и отведенного тепла, если:Р1=1 бар; t1=20оC, = 3,6; = 3,33; k = 1,4. Рабочее тело – воздух. Теплоемкость принять постоянной.
Решение
Расчет ведемдля I кгвоздуха.
Точка 1: P1=1бар; t1=20oС. Удельный объем определяем из уравнения состояния (15):
Точка 2. Удельный объем находим исходя из степени сжатия
Температура в конце адиабатного сжатия определяется из соотношения
Давление в конце адиабатного сжатия определяем по характеристическому уравнению (15)
Точка 3. Удельный объем v3=v2=0,233 м3/кг. Из соотношения параметров в изохорном процессе (линия 2-3) получаем
Следовательно,
Точка 4. Удельный объем v4=v1=0,84 м3/кг. Температура в конце адиабатного расширения – уравнение (78)
Давление в конце адиабатного расширения определяем из соотношения параметров в изохорном процессе (линия 4-1):
Определяем количество подведенного и отведенного тепла
Термический КПД цикла определяем по формуле (111)
или по формуле (115)
Работа цикла
54. В идеальном одноступенчатом компрессоре массовой производительностью G=180 кг/чсжимается воздух до давления Р2=4,9 бар.Определить теоретически необходимую мощность электродвигателя компрессора, отведенное в рубашку цилиндра компрессора тепло и расход охлаждающей воды, если сжатие происходит политропно (п=1,3), а охлаждающая вода нагревается на 25°С. Начальное давление воздуха Р1=0,98 бари температура t1=0С.
Решение
Работа, расходуемая на сжатие 1 кг газа в одноступенчатом компрессоре при политермическом режиме, определяется по формуле (125)
Мощность, расходуемая на сжатие газа в компрессоре, определяем по формуле (129)
Удельное количество отведенной теплоты определяем по формуле (85)
Температуру в конце политропного сжатия определяем из соотношения (83)
Определяем полное количество отведенной теплоты
Расход охлаждающей воды составляет
55. Определить расход воды на охлаждение воздуха в рубашке двухступенчатого компрессора производительностью 10 м3/мин.в промежуточном и концевом холодильниках, если в холодильниках воздух охлаждается до начальной температуры, а вода нагревается на 15С. Воздух перед компрессором имеет давление Р1=0,98 бари температуру t1=10С, сжатие воздуха в компрессоре происходит политропно (п=1,3) до конечного давления Р2=8,8 бар.
Решение
Количество тепла, отводимого в рубашке компрессора
от 1 кгвоздуха,
;
от G кгвоздуха
.
Количество тепла, отводимого в промежуточном и концевом холодильниках: от 1 кгвоздуха
;
от G кг воздуха
.
Массовую производительности компрессора определяем из характеристического уравнения (15)
.
Промежуточное давление – уравнения (132) и (133)
.
Температура в конце сжатия – уравнение (83)
.
Количество тепла, отводимого в рубашке .компрессора,
.
Количество тепла, отводимого в промежуточном и концевом холодильниках,
.
Расход охлаждающей воды
.
Истечение газов и паров. Дросселирование
1 ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
Источник
