Как найти площадь цилиндрического сосуда
Определение цилиндра
Цилиндр – геометрическое тело, которое можно получить при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор
На самом деле, это определение только самого простого, кругового цилиндра. Более общее определение цилиндрического тела следующее:
Цилиндром называют тело, образованное пересечением параллельных друг другу прямых и двух плоских поверхностей.
Такие прямые называются образующими данного цилиндра.
Прямая, перпендикулярная обоим основаниям, является высотой цилиндра.
Плоские поверхности называют основаниями данного цилиндра. Часто, они параллельны друг другу, но не всегда.
Виды цилиндра
Виды цилиндра зависят от того, под каким углом пересекаются образующие и основания нашего тела.
Если угол равен 90 градусам, то получим, так называемый, прямой цилиндр. У него есть ось симметрии – это перпендикуляр, соединяющий центры его оснований.
Если угол другой, то цилиндр называется наклонным.
Если форма основания – гипербола, то цилиндр гиперболический, если парабола – параболический, если эллипс – эллиптический, если круг – круговой.
Если основания цилиндра не параллельны, то он называется косым.
Формула площади поверхности цилиндра
Полная площадь поверхности цилиндра является суммой его боковой площади поверхности и площади оснований.
S = S осн + S бок S=S_{text{осн}}+S_{text{бок}} S=Sосн+Sбок
S осн S_{text{осн}} Sосн – площадь оснований;
S бок S_{text{бок}} Sбок – площадь боковой поверхности.
При вычислении площади поверхности цилиндра важным фактором является вид цилиндра. От него зависит и конкретная формула для площади.
Формула площади поверхности кругового цилиндра
S осн = 2 ⋅ π ⋅ r 2 S_{text{осн}}=2cdotpicdot r^2 Sосн=2⋅π⋅r2
S бок = 2 ⋅ π ⋅ r ⋅ h S_{text{бок}}=2cdotpicdot rcdot h Sбок=2⋅π⋅r⋅h
r r r – радиус круга (основания кругового цилиндра);
h h h – высота этого цилиндра.
Сокращенно, это формулу можно записать так:
S = S осн + S бок = 2 ⋅ π ⋅ r 2 + 2 ⋅ π ⋅ r ⋅ h = 2 ⋅ π ⋅ r ⋅ ( r + h ) S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+2cdotpicdot rcdot h=2cdotpicdot rcdot(r+h) S=Sосн+Sбок=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)
Пример
Радиус круга, лежащего в основании прямого кругового цилиндра, имеет длину 6 (см.). Высота цилиндра – 20 (см.). Найдите полную площадь его поверхности.
Решение:
r = 6 r=6 r=6
h = 20 h=20 h=20
По формуле:
S = 2 ⋅ π ⋅ r ⋅ ( r + h ) = 2 ⋅ π ⋅ 6 ⋅ ( 6 + 20 ) ≈ 979 , 68 S=2cdotpicdot rcdot(r+h)=2cdotpicdot 6cdot(6+20)approx979,68 S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68 (см. кв.)
Ответ: 979,68 см. кв.
Формула площади поверхности наклонного кругового цилиндра
S осн = 2 ⋅ π ⋅ r 2 S_{text{осн}}=2cdotpicdot r^2 Sосн=2⋅π⋅r2
S бок = p ⋅ l S_{text{бок}}=pcdot l Sбок=p⋅l
r r r – радиус круга (основания кругового цилиндра);
p p p – периметр сечения наклонного цилиндра перпендикулярно образующей;
l l l – длина образующей этого цилиндра.
Пример
Найти площадь поверхности наклонного цилиндра, если периметр p p p сечения плоскости, составляющей прямой угол с образующей, равен 30 (см.), а сама образующая равна 7 (см.) Радиус окружности, лежащей в основе цилиндра в два раза меньше его образующей.
Решение:
r = l 2 r=frac{l}{2} r=2l
p = 30 p=30 p=30
l = 7 l=7 l=7
Найдем сначала радиус основания:
r = l 2 = 7 2 = 3.5 r=frac{l}{2}=frac{7}{2}=3.5 r=2l=27=3.5
Тогда полная площадь:
S = S осн + S бок = 2 ⋅ π ⋅ r 2 + p ⋅ l = 2 ⋅ π ⋅ 3. 5 2 + 30 ⋅ 7 ≈ 76 , 93 + 210 = 286 , 93 S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+pcdot l=2cdotpicdot 3.5^2+30cdot 7approx76,93+210=286,93 S=Sосн+Sбок=2⋅π⋅r2+p⋅l=2⋅π⋅3.52+30⋅7≈76,93+210=286,93 (см. кв.)
Ответ: 286,93 см. кв.
Тест по теме «Площадь поверхности цилиндра»
Источник
Площадь цилиндра – как правильно рассчитать
Определение
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.
Перед тем, как начать вычисление площади цилиндра, необходимо учесть, что существует два ее вида:
- Полная площадь поверхности цилиндра. Она равна сумме боковой поверхности цилиндра и двойной площади его основания.
- Площадь боковой поверхности цилиндра. Она равняется произведению высоты цилиндра на длину окружности основания.
Чтобы вычислить общую площадь поверхности цилиндра, нужно применить формулу:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(S=2spis Rs h+2spis R^2=2spis Rsleft(h+Rright))
Здесь R – радиус окружности, а h – высота.
Чтобы найти площадь боковой поверхности цилиндра, нужно воспользоваться формулой:
(S=2spis Rs h)
«Компоненты» стереометрической фигуры
Цилиндр состоит из нескольких составляющих.
- Цилиндрическая поверхность – это поверхность, которая образуется большим количеством параллельных прямых, проходящих через точки некоторой кривой.
- Основания – это плоские фигуры, которые образованы пересечением ЦП с двумя параллельными плоскостями, ограничивающими цилиндр. Оснований у цилиндра два.
- Боковой поверхностью называют часть ЦП, которая находится между основаниями.
- И, наконец, высота – это отрезок, который высекается плоскостями оснований цилиндра на прямой, перпендикулярной им.
Примечание
Дополнительно можно измерить периметр Sбок. Для этого нужно длину окружности l сложить с высотой h и умножить данную сумму на 2.
Рассмотрим, как различаются типы рассматриваемой геометрической фигуры по форме. Цилиндр может быть:
- Прямой. Его основания имеют центры симметрии, то есть являются кругами или эллипсами. При этом прямая между центрами перпендикулярна плоскостям оснований. Данная прямая называется осью цилиндра.
- Косой. Его основания имеют центры симметрий, однако отрезок между ними не перпендикулярен плоскостям оснований.
- Круговой. Имеет окружность в роли направляющей.
- Прямой круговой. Его можно получить с помощью вращения прямоугольника вокруг одной из его сторон. Тогда эта сторона будет осью цилиндра и осью симметрии.
- Равносторонний. Его диаметр равен высоте.
- Эллиптический, гиперболический и параболический. Образованы соответственно эллипсами, гиперболами и параболами.
- Усеченный. Геометрическое тело, которое отсекается от цилиндра плоскостью, не параллельной основанию.
- Призма. Является разновидностью цилиндра, если имеет основание в виде многоугольника.
Основные формулы для вычисления боковой и полной площади
Кроме рабочих способов, перечисленных выше, рассчитать площадь рассматриваемого тела можно следующими методами:
- Через диаметр и высоту: ( S_{полн.}=Dspileft(h+frac D2right); S_{бок.}=Dspis h.)
- Через объем: (S=frac Vh.)
- Через длину окружности. Так как (l=2spis R), то (S_{бок.}=ls h), а (S_{полн.}=ls h+2spis R^2).
Приведем примеры расчета.
Задача 1
Радиус основания цилиндра равен 2, высота равна 3. Высчитать площадь боковой поверхности цилиндра.
Решение
(S_{бок.}=2spis Rs h)
Из этого: (S_{бок.}=2s3,14s2s3=6,28s6=37,68.)
Ответ: (S_{бок.}=37,68.)
Задача 2
(S_{бок.}=24pi), а диаметр основания – 3. Узнать высоту цилиндра.
Решение
(S_{бок.}=2spis Rs h)
Высоту отсюда вычислим так:
(h=frac{S_{бок.}}{2pi R})
Радиус равен: (R=frac D2. h=frac{24pi}{2pis0,5D}=frac{24pi}{2pis0,5s3}=frac{12}{1,5}=8)
Ответ: (h=8.)
Источник
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики – более 33 лет.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.
Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr2 + πr2 = 2πr2.
Боковая поверхность цилиндра
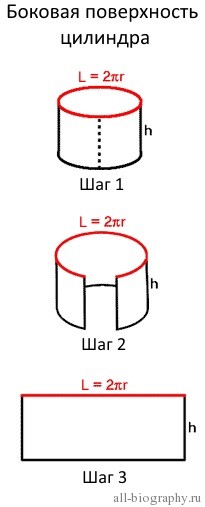
 Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
Sбок. = 2πrh
r – радиус цилиндра, h – высота цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь боковой поверхности рассчитывается по формуле: Sбок. = 2πrh
Sбок. = 2 * 3,14 * 2 * 3
Sбок. = 6,28 * 6
Sбок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr2 + 2πrh
S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
S = 376,8
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания – 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:
h = Sбок./2πr
Значение радиуса получаем из формулы: d = 2r
h = 24π / (2π * 0,5d)
h = 24π / (2π * 0,5 * 3)
h = 12 / 1,5
h = 8
Высота цилиндра равна 8.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Dark Spyro
5/5
Татьяна Матвиенко
5/5
Юрий Евдокимов
5/5
Михаил Чепурной
5/5
Дмитрий Новиков
5/5
Дилноза Саипова
4/5
Darya Simonova
5/5
Тамара Иванова
5/5
Татьяна Немчинова
5/5
Рамиль Сагиров
5/5
Оценка статьи
Средняя оценка: 4.6. Всего получено оценок: 9312.
Источник
