Как найти сколько килограмм кислоты в сосуде
ÐадаÑа â807 из 1084 |
ÐмеÑÑÑÑ Ð´Ð²Ð° ÑоÑÑда, ÑодеÑжаÑие 10 кг и 16 кг ÑаÑÑвоÑа киÑлоÑÑ ÑазлиÑной конÑенÑÑаÑии. ÐÑли Ð¸Ñ ÑлиÑÑ Ð²Ð¼ÐµÑÑе, Ñо полÑÑиÑÑÑ ÑаÑÑвоÑ, ÑодеÑжаÑий 55% киÑлоÑÑ. ÐÑли же ÑлиÑÑ ÑавнÑе маÑÑÑ ÑÑÐ¸Ñ ÑаÑÑвоÑов, Ñо полÑÑеннÑй ÑаÑÑÐ²Ð¾Ñ Ð±ÑÐ´ÐµÑ ÑодеÑжаÑÑ 61% киÑлоÑÑ. СколÑко килогÑаммов киÑлоÑÑ ÑодеÑжиÑÑÑ Ð² пеÑвом ÑаÑÑвоÑе?
РеÑение задаÑи:
Ðведем обознаÑениÑ:
x – конÑенÑÑаÑÐ¸Ñ ÐºÐ¸ÑлоÑÑ Ð² пеÑвом ÑоÑÑде.
10x – маÑÑа киÑлоÑÑ Ð² 10 кг ÑаÑÑвоÑа в пеÑвом ÑоÑÑде, Ñ.е. Ñо ÑÑо надо найÑи в задаÑе.
y – конÑенÑÑаÑÐ¸Ñ ÐºÐ¸ÑлоÑÑ Ð²Ð¾ вÑоÑом ÑоÑÑде.
16y – маÑÑа киÑлоÑÑ Ð² 16 кг ÑаÑÑвоÑа во вÑоÑом ÑоÑÑде.
СоÑÑавим ÑÑавнение Ð´Ð»Ñ Ð¿ÐµÑвого ÑÑловиÑ:
10x+16y=26*0,55 (26 – ÑÑо маÑÑа нового ÑаÑÑвоÑа 10+16, 0,55 – конÑенÑÑаÑÐ¸Ñ Ð½Ð¾Ð²Ð¾Ð³Ð¾ ÑаÑÑвоÑа).
10x+16y=14,3
10x=14,3-16y
СоÑÑавим ÑÑавнение Ð´Ð»Ñ Ð²ÑоÑого ÑÑловиÑ:
10x+10y=20*0,61
10x+10y=12,2
ÐодÑÑавлÑем во вÑоÑое ÑÑавнение знаÑение 10Ñ
:
14,3-16y+10y=12,2
14,3-6y=12,2
6y=14,3-12,2
6y=2,1
y=0,35
ÐодÑÑавлÑем знаÑение y в пеÑвое ÑÑавнение:
10x=14,3-16y
10x=14,3-16*0,35
10x=8,7
ÐÑвеÑ: 8,7
ÐоделиÑеÑÑ ÑеÑением
ÐÑиÑоединÑйÑеÑÑ Ðº нам…
ÐÑ Ð¼Ð¾Ð¶ÐµÑе поблагодаÑиÑÑ Ð°Ð²ÑоÑа, напиÑаÑÑ Ñвои пÑеÑензии или пÑÐµÐ´Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°
ÑÑÑаниÑе ‘ÐÑо нађ
ÐÑÑгие задаÑи из ÑÑого Ñаздела

ÐадаÑа âF92A32
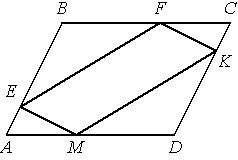 РпаÑаллелогÑамме ÐÐСD ÑоÑки E, F, K и Ð Ð»ÐµÐ¶Ð°Ñ Ð½Ð° его ÑÑоÑонаÑ
, как показано на ÑиÑÑнке, пÑиÑÑм СF = ÐM, BE = DK. ÐокажиÑе, ÑÑо EFKM â паÑаллелогÑамм.
РпаÑаллелогÑамме ÐÐСD ÑоÑки E, F, K и Ð Ð»ÐµÐ¶Ð°Ñ Ð½Ð° его ÑÑоÑонаÑ
, как показано на ÑиÑÑнке, пÑиÑÑм СF = ÐM, BE = DK. ÐокажиÑе, ÑÑо EFKM â паÑаллелогÑамм.

ÐадаÑа â3A1860
 ÐлоÑÐ°Ð´Ñ Ð¿ÑÑмоÑголÑного ÑÑеÑголÑника Ñавна 968√3. Ðдин из оÑÑÑÑÑ
Ñглов Ñавен 60°. ÐайдиÑе Ð´Ð»Ð¸Ð½Ñ ÐºÐ°ÑеÑа, пÑилежаÑего к ÑÑÐ¾Ð¼Ñ ÑглÑ.
ÐлоÑÐ°Ð´Ñ Ð¿ÑÑмоÑголÑного ÑÑеÑголÑника Ñавна 968√3. Ðдин из оÑÑÑÑÑ
Ñглов Ñавен 60°. ÐайдиÑе Ð´Ð»Ð¸Ð½Ñ ÐºÐ°ÑеÑа, пÑилежаÑего к ÑÑÐ¾Ð¼Ñ ÑглÑ.

ÐадаÑа â956EDE
ÐайдиÑе плоÑÐ°Ð´Ñ Ð¿Ð°ÑаллелогÑамма, изобÑажÑнного на ÑиÑÑнке.

ÐадаÑа âA1451C
ÐÑÑмаÑ, паÑаллелÑÐ½Ð°Ñ ÑÑоÑоне AC ÑÑеÑголÑника ABC, пеÑеÑÐµÐºÐ°ÐµÑ ÑÑоÑÐ¾Ð½Ñ AB и BC в ÑоÑÐºÐ°Ñ M и N ÑооÑвеÑÑÑвенно, AC=44, MN=24. ÐлоÑÐ°Ð´Ñ ÑÑеÑголÑника ABC Ñавна 121. ÐайдиÑе плоÑÐ°Ð´Ñ ÑÑеÑголÑника MBN.

ÐадаÑа â01130C
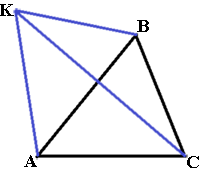 СÑоÑÐ¾Ð½Ñ AC, AB, BC ÑÑеÑголÑника ABC ÑÐ°Ð²Ð½Ñ 2√5, √11 и 2 ÑооÑвеÑÑÑвенно. ТоÑка K ÑаÑположена вне ÑÑеÑголÑника
СÑоÑÐ¾Ð½Ñ AC, AB, BC ÑÑеÑголÑника ABC ÑÐ°Ð²Ð½Ñ 2√5, √11 и 2 ÑооÑвеÑÑÑвенно. ТоÑка K ÑаÑположена вне ÑÑеÑголÑника
ABC, пÑиÑÑм оÑÑезок KC пеÑеÑÐµÐºÐ°ÐµÑ ÑÑоÑÐ¾Ð½Ñ AB в ÑоÑке, оÑлиÑной Ð¾Ñ B. ÐзвеÑÑно, ÑÑо ÑÑеÑголÑник Ñ Ð²ÐµÑÑинами K, A и C подобен иÑÑ
одномÑ. ÐайдиÑе коÑинÑÑ Ñгла AKC, еÑли ∠KAC>90°.
Источник
Математику нельзя изучать,
наблюдая, как это делает сосед.
А.Нивен.
Цель урока: Создание условий для выработки
алгоритма решения задач на смеси, сплавы,
растворы.
Задачи урока:
Обучающие:
- Обобщение и систематизация знаний, умений и
навыков учащихся по теме “Решение задач на
смеси, сплавы, растворы”; - Формирование умений и навыков применения
знаний в нестандартной ситуации.
Развивающие:
- Способствовать развитию внимания, логического
мышления, самостоятельной учебно-познавательной
деятельности.
Воспитывающие: Воспитывать математическую
культуру, ответственность, настойчивость в
учебе.
Тип урока: практикум по решению задач.
Формы работы учащихся: коллективная,
индивидуальная.
Оборудование: Компьютер,
мультимедиа-проектор, дидактический раздаточный
материал.
Ход урока
1. Организационный момент.
Эпиграф СЛАЙД 2
– Сообщение темы урока. СЛАЙД 3
– Постановка цели урока.
2. Подготовительный этап.
Повторение теоретического материала о
процентах: СЛАЙД 4
– Что такое процент? (Сотая часть числа)
– Как перевести проценты в дробь? (Разделить
количество процентов на 100)
– Как перевести дробь в проценты? (Умножить
данную дробь на 100)
– Как найти проценты от данного числа? (Проценты
перевести в дробь и умножить данное число на эту
дробь)
– Как найти число по его процентам? (Проценты
перевести в дробь и разделить данное число на эту
дробь)
– Как найти процентное отношение двух чисел?
(Первое число разделить на второе и результат
умножить на 100)
– Что такое концентрация вещества? (Это
величина, которая определяет содержание
компонента в сплаве, смеси, растворе)
3. Закрепление материала. Решение задач.
Рассмотрим способы решения задач:
арифметический, с помощью уравнения и с помощью
систем уравнений. СЛАЙД 5
Арифметический способ.
СЛАЙД 6. Задача 1. В сосуд, содержащий 5 литров 12
процентного водного раствора некоторого
вещества, добавили 7 литров воды. Сколько
процентов составляет концентрация
получившегося раствора?
Рассмотрим три способа решения этой задачи.
Первый способ.
объем
получившегося раствора
объем
чистого вещества в первом растворе.
концентрацияполучившегося раствора.
Второй способ. По формуле.
где концентрация
первого и второго растворов соответственно.
объемы
первого и второго растворов соответственно
Третий способ.
Объем раствора увеличился в 2,4 раза (было 5 л.,
стало 12 л. 12:5 = 2,4),
содержание вещества не изменилось, поэтому
процентная концентрация получившегося раствора
уменьшилась в 2,4 раза.12:2,4=5(%)
Ответ: 5 %.
СЛАЙД 7. Задача 2. Сколько литров воды нужно
добавить в 2 л водного раствора, содержащего 60%
кислоты, чтобы получить 20 процентный раствор
кислоты?
Объем чистой кислоты в растворе не меняется,
процентное содержание кислоты в растворе
уменьшится в 3 раза (60:20=3)
Объем раствора увеличится в 3 раза: 2 * 3=6(л)
6 – 2 = 4 (л) воды нужно добавить.
Ответ: 4 л.
СЛАЙД 8. Задача 3. Смешали 4 литра 15 процентного
водного раствора с 6 литрами 25 процентного
водного раствора этого же вещества. Сколько
процентов составляет концентрация
получившегося раствора?
Рассмотрим два способа решения этой задачи.
Первый способ. По формуле.
где концентрация
первого и второго растворов соответственно.
объемы
первого и второго растворов соответственно.
Второй способ.
объем
получившегося раствора.
объем
чистого вещества в четырех литрах раствора.
объем
чистого вещества в шести литрах раствора.
объем
чистого вещества в получившемся растворе.
концентрация получившегося раствора.
Ответ: 21%
СЛАЙД 9. Задача 4. Влажность сухой цементной
смеси на складе составляет 18%. Во время перевозки
из-за дождей влажность смеси повысилась на 2%.
Найдите массу привезенной смеси, если со склада
было отправлено 400 кг.
воды в
цементе на складе.
сухого
вещества в цементе на складе.
сухого
вещества в цементе в 328 килограммах.
масса
привезенной смеси.
Ответ: 410 кг.
Минута отдыха.
Напишите в воздухе кончиком носа свою фамилию и
имя.
Решение задач с помощью уравнения.
СЛАЙД 10. Задача 5. Сколько надо взять 5
процентного и 25 процентного раствора кислоты,
чтобы получить 4 л 10 процентного раствора
кислоты?
0,1· 4=0,4(л) – кислоты в новом растворе.
Пусть х л надо взять первого раствора. Тогда
второго – (4 – х) л, а количество
получившегося раствора 2х.
0,05х л – кислоты в первом растворе.
0,25· (4 – х) л – кислоты во втором растворе.
0,05х + 0,25· (4 – х) = 0.05х + 1 – 0,25х = (1 –
0,2х) л.
Получим уравнение
3 л надо взять первого раствора.
4 – 3 = 1 л – второго.
Ответ: 1 л, 3 л.
СЛАЙД 11. Задача 6. В сосуд емкостью 6л налито 4л
70% раствора серной кислоты. Во второй сосуд той же
емкости налито 3л 90% раствора серной кислоты.
Сколько литров раствора нужно перелить из
второго сосуда в первый, чтобы в нем получился 74%
раствор серной кислоты? Найдите все допустимые
значения процентного содержания раствора серной
кислоты в 6л раствора в первом сосуде.
Пусть х литров раствора кислоты нужно
перелить из второго сосуда в первый. Тогда в нем
станет (4 + х) литров 74 процентного раствора.
кислоты в
первом сосуде.
(0,9х) литров – кислоты нужно перелить.
(2,8 + 0,9х) литров – кислоты в новом растворе.
Учитывая, что новый раствор 74% и его объем (4 + х)
литров, то кислоты в нем (0,74·(4 + х )) литров.
Получим уравнение:
Найдем допустимые значения процентного
содержания.
Так как в первый сосуд налит 70 процентный
раствор серной кислоты, а будем доливать 90
процентный раствор, то процентное содержание
раствора будет увеличиваться.
Из второго сосуда в первый можно перелить
максимальное количество раствора кислоты – 2
литра.
кислоты в
двух литрах.
кислоты
будет в первом сосуде.
Тогда процентное содержание раствора серной
кислоты в шести литрах раствора в первом сосуде
может быть
Ответ: 1;
СЛАЙД 12. Задача 7. Первый сплав содержит 10%
меди, второй – 40% меди. Масса второго сплава
больше массы первого на 3кг. Из этих двух сплавов
получили третий сплав, содержащий 30% меди.
Найдите массу третьего сплава. Ответ дайте в
килограммах.
Пусть х кг масса первого сплава. Тогда масса
второго сплава (х + 3) кг, а масса третьего
сплава (х + (х + 3)) = (2х + 3) кг.
Масса меди в первом сплаве (0,1х) кг, во втором
– (0,4·(х + 3)) кг, а в третьем – (0,3· (2х +3)) кг.
Получим уравнение:
3 кг масса первого сплава.
2 · 3 + 3 = 9 (кг) – масса третьего сплава.
Ответ: 9 кг.
СЛАЙД 13. Задача 8. Имеется два сплава золота и
серебра: в одном массы этих металлов находятся в
отношении 2:3, а в другом – в отношении 3:7. Сколько
килограммов нужно взять от каждого сплава, чтобы
получить 8 кг нового сплава, в котором золото и
серебро находились бы в отношении 5:11?
Пусть х кг масса куска, взятого от первого
сплава. Тогда масса куска, взятого от второго
сплава (8 – х) кг.
Масса золота в первом куске
Масса золота во втором куске
Масса золота в новом сплаве
Получим уравнение
1 кг нужно взять от первого сплава.
8 – 1 = 7 (кг) – от второго сплава.
Ответ: 1кг; 7 кг.
В этой задаче можно было бы составить и другие
уравнения
*
*
*
Решение задач с помощью систем уравнений
СЛАЙД 14. Задача 9. Имеется два сплава. Первый
содержит 10% никеля, второй- 30% никеля. Из этих двух
сплавов получили третий сплав массой 200 кг,
содержащий 25% никеля. На сколько килограммов
масса первого сплава меньше массы второго?
Пусть х кг масса первого сплава, у кг –
второго.
Так как масса третьего сплава 200 кг, то получим
уравнение
Масса никеля в первом сплаве (0,1х) кг, во
втором – (0,3у) кг, а в новом – 200·0,25=50 кг. Получим
второе уравнение
Получим систему уравнений:
50 кг – масса первого сплава.
150 кг – масса второго сплава.
150 – 50 = 100 (кг)
Ответ: на 100 кг.
СЛАЙД 15. Задача 10. При смешивании 30
процентного раствора серной кислоты с10
процентным раствором серной кислоты получилось
400 г 15 процентного раствора. Сколько граммов 30
процентного раствора было взято?
Пусть х г масса 30 процентного раствора
серной кислоты, а у г – 10 процентного. Получим
уравнение х + у = 400.
кислоты в
новом растворе.
кислоты в
первом растворе.
кислоты во
втором растворе.
Получим второе уравнение
Получим систему уравнений:
100 г 30 процентного раствора было взято.
Ответ:100 г.
Слайд 16. Задача 11. Имеются два слитка сплава
серебра и олова. Первый слиток содержит 360г
серебра и 40г олова, а второй слиток – 450г серебра
и 150г олова. От каждого слитка взяли по куску,
сплавили их и получили 200г сплава, в котором
оказалось 81% серебра. Определите массу (в граммах)
куска, взятого от второго слитка.
Первый слиток имеет вес 400 г, второй – 600 г.
серебра в
первом слитке (соответственно и в первом куске).
серебра во
втором слитке (соответственно и во втором куске).
Пусть х г масса куска, взятого от первого
слитка, а у г – от второго.
0,9х (г) – серебра в первом куске;
0,75у (г) – серебра во втором куске;
200 * 0,81 = 162 (г) – серебра в новом сплаве.
Получим систему уравнений:
120 г нужно взять от второго слитка.
Ответ: 120 г.
СЛАЙД 17. Задача 14. Первый раствор содержит 40%
кислоты, а второй – 60% кислоты. Смешав эти растворы
и добавив 5 л воды, получили 20 процентный раствор.
Если бы вместо воды добавили 5 л 80 процентного
раствора, то получился бы 70 процентный раствор.
Сколько литров 60 процентного раствора кислоты
было первоначально?
Пусть х л было 40 процентного, а у л – 60
процентного раствора кислоты. Тогда нового, 20
процентного раствора – (х + у + 5) л.
0,4х (л) – кислоты в первом растворе;
0,6у (л) – кислоты во втором растворе;
0,2·(х + у + 5) (л) – кислоты в новом растворе.
Получим уравнение
кислоты в 80
процентном растворе;
кислоты в
новом, 70 процентном растворе.
Получим второе уравнение
Получим систему уравнений:
2 л 60 процентного раствора было первоначально.
Ответ: 2 л.
Контроль знаний. Самостоятельная работа.
Учащиеся выполняют работу по карточкам и сдают
на проверку.
Приложение 1
Домашнее задание.
Даются карточки с дифференцированными
заданиями.
Приложение 2
Источник
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
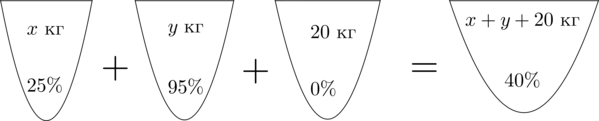
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
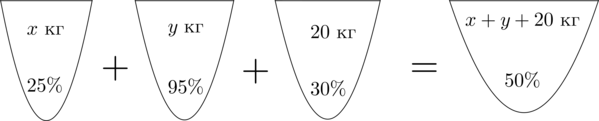
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20
Источник
