Как найти установившуюся температуру в сосуде

Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
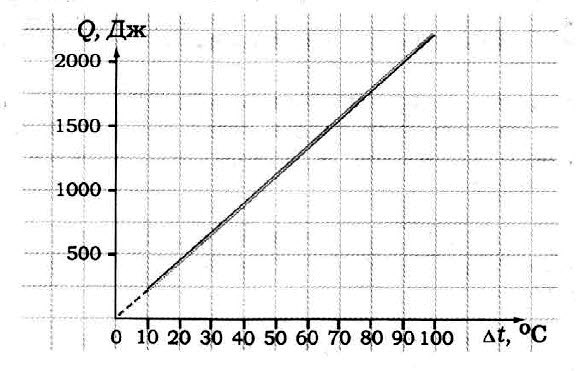

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
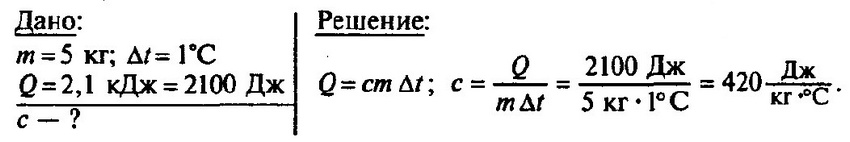
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
Задача по физике – 12036
На дне стакана с водой лежат несколько запаянных с одного конца и заполненных воздухом капиллярных трубок. Диаметр трубок $d = 0,2 мм$, высота уровня воды в стакане $h = 10 см$. При кипении воды у открытых концов трубок образуются пузырьки пара. Чему равна температура воды на дне стакана, если атмосферное давление равно $10^{5} н/м^{2}$. Коэффициент поверхностного натяжения воды принять равным $57 дин/см$. Считать, что давление насыщенных паров воды вблизи $100^{ circ} С$ возрастает на 27 мм. рт. ст. при повышении температуры на $1^{ circ}$.
Подробнее
Задача по физике – 12043
Найти радиус наибольшей капли воды, которая может испариться, не поглотив тепла извне.
Подробнее
Задача по физке – 12048
В расположенном вертикально цилиндре переменного сечения (рис.) между поршнями находятся $n$ молей воздуха. Массы поршней $m_{1}$ и $m_{2}$, их площадей $S_{1}$ и $S_{2}$ соответственно. Поршни соединены стержнем длины $l$ и находятся на одинаковых расстояниях от стыка частей цилиндра с различными диаметрами. На сколько сместятся поршни при повышении температуры в цилиндре на $Delta t$ градусов?

Подробнее
Задача по физке – 12050
Два запаянных сообщающихся капиллярных сосуда цилиндрической формы разных диаметров частично заполнены водой (ртутью) (рис.). Воздух из сосудов откачан, так что над жидкостью имеются только ее пары. Как распределится количество жидкости в сосудах: а) на земле? б) в невесомости?

Подробнее
Задача по физке – 12053
Устройство ртутного медицинского термометра показано на рисунке. К баллончику со ртутью припаян тонкий капилляр, внизу которого имеется “перетяжка” – участок с диаметром примерно 30 микрон. Какую роль играет эта перетяжки? Оцените, какое ускорение нужно сообщить термометру для того, чтобы его встряхнуть, после изменения температуры?

Подробнее
Задача по физке – 12055
Имеется следующий проект летательного аппарата. Верхняя поверхность большой плоской пластинки поддерживается при постоянной температуре $0^{ circ} С$, а нижняя – при температуре $100^{ circ} С$. Изобретатель утверждает, что такая пластинки будет висеть в воздухе подобно дирижаблю. Объясните, почему. Оцените по порядку величины подъемную силу такой пластинки с площадью $1 м^{2}$ при температуре воздуха $20^{ circ} С$.
Подробнее
Задача по физке – 12064
В электровакуумном приборе чистый вольфрамовый катод находится в большой колбе, содержащей остатки кислорода при давлении $p = 10^{-7} атм$ и температуре $T = 300^{ circ} К$. Считая, что каждая молекула, попавшая на катод, прилипает к нему, оценить время образования мономолекулярного слоя. Молекулы можно считать шариками диаметром $d approx З cdot 10^{-8} см$.
Подробнее
Задача по физке – 12070
В теплоизолированном баллоне находится 5 г водорода и 12 г кислорода. Смесь поджигают. Определить давление и температуру в сосуде, если известно, что при образовании 1 моля воды выделяется количество теплоты $Q_{0} = 2,4 cdot 10^{5} дж$. Объем сосуда 100 литров. Начальная температура смеси кислорода и водорода $t_{0} = 20^{ circ} С$. Удельная теплоемкость водорода при постоянном объеме равна $c_{в} = 14,3 кдж/(кг cdot град)$, а водяных паров – $c_{п} = 2,1 кдж/(кг cdot град)$.
Подробнее
Задача по физке – 12071
Сложенные вместе смоченные оконные стекла практически невозможно отделить друг от друга, пытаясь оторвать одно стекло от другого. Почему?
Подробнее
Задача по физке – 12080
Стенки цилиндра, поршень и внутренняя перегородка площадью $1 дм^{3}$ изготовлены из теплоизоляционного материала (рис.). Клапан в перегородке открывается в том случае, если давление справа больше давления слева. В начальном состоянии в левой части цилиндра длиной $l = 11,2 дм$ находится $m_{1} = 12 г$ гелия, в правой части, имеющей ту же длину, – $m_{2} = 2 г$ гелия, с обеих сторон температура равна $t_{0} = 0^{ circ} С$ ($T_{0} = 273^{ circ} К$). Внешнее давление $p_{0} = 10^{5} н/м^{2}$. Удельная теплоемкость гелия при постоянном объеме $c_{V} = 3,15 cdot 10^{3} дж/(кг cdot град)$, а при постоянном давлении $c_{p} = 5,25 cdot 10^{3} дж/ (кг cdot град)$. Поршень медленно передвигается по направлению к перегородке (с небольшой остановкой в момент открытия клапана) и осторожно доводится до перегородки. Чему равна произведенная при этом работа? Площадь поршня $S = 10^{-2} м^{2}$.

Подробнее
Задача по физке – 12087
Оцените приближенно, при каком минимальном радиусе планеты она сможет удерживать атмосферу, состоящую в основном из кислорода и азота, если температура поверхности планеты $T = 300 К$. Среднюю плотность вещества планеты принять равной $rho = 4 cdot 10^{3} кг/м^{3}$.
Подробнее
Задача по физке – 12105
На рисунке изображены два замкнутых цикла: АБВА и АВГА. Оба цикла проведены с идеальным одноатомным газом.
1) Указать, на каких участках циклов газ получает и на каких участках отдает тепло.
2) У какого из циклов коэффициент полезного действия выше? Во сколько риз?

Подробнее
Задача по физке – 12110
Теплоизолированная полость небольшими одинаковыми отверстиями соединена с двумя объемами, содержащими газообразный гелий (рис.). Давление гелия в этих объемах поддерживается постоянным и равным $p$, а температуры поддерживаются равными $T$ в одном из объемов и $2T$ в другом. Найти установившиеся давление и температуру внутри полости.

Подробнее
Задача по физке – 12113
Природный уран состоит из смеси двух изотопов с относительными атомными массами 235 и 233 и отношением концентраций 7 : 1000. Для увеличения концентрации $^{235} U$, который применяется в атомных реакторах, используется истечение газообразного соединения $UF_{6}$ (шестифтористый уран) о вакуум через маленькие отверстия (эффузия). Газ пропускается через трубу Т с пористыми стенками (рис.). Прошедший через стенки трубы газ откачивается из сосуда С. Определить отношение концентраций $^{235} UF_{6}$ и $^{238}UF_{6}$ в откачиваемом газе. Относительная масса фтора равна 19.

Подробнее
Задача по физке – 12116
Для определения неизвестного объема $V_{1}$ баллона I собирают схему, приведенную на рисунке. Объем баллона II равен $V_{2}$ и $V_{2} ll V_{1}$. Сначала систему откачивают до давления $p_{0}$, близкого к нулю. Затем закрывают кран В и заполняют биллон II газом до давления $p_{0}$. После этого закрывают крон A, открывают кран В и измеряют установившееся в системе давление $p_{1}$ манометром С. Затем при закрытом кране В вновь наполняют баллон газом до давления $p_{0}$, открывают кран В и измеряют установившиеся в системе давление $p_{2}$. Эту операцию повторяют $n$ раз. Покажите, что отношение $frac{p_{n} – p_{)} }{np_{0} }$ – есть величина постоянная и равная $frac{V_{2} }{V_{1} + V_{2} }$.

Подробнее
Источник
Задача по физике – 12661
В кастрюлю-скороварку налили немного воды. закрыли герметично и поставили на огонь. К тому моменту, когда вся вода испарилась, температура кастрюли оказалась $115^{ circ} С$, а давление внутри – 3 атмосферы. Какую часть объема вначале занимала вода? Начальная температура $20^{ circ} С$.
Подробнее
Задача по физике – 12669
Тонкая квадратная пластинка АБВГ сделана из меди. Ее нагревают со стороны торца АБ, поддерживая его температуру равной $100^{ circ} С$, и охлаждают со стороны трех остальных торцов, поддерживая их температуру равной $0^{ circ} С$. Найдите температуру в центре пластинки.
Подробнее
Задача по физике – 12670
Внутри длинной трубы, наполненной воздухом, двигают с постоянной скоростью поршень, при этом в трубе распространяется со скоростью 320 м/с упругая волна. Считая перепад давлений на границе распространения волны равным 1000 Па, оцените перепад температур. Давление в невозмущенном воздухе 1 атм, температура 300 К.
Подробнее
Задача по физике – 12674
Внутри большого мыльного пузыря находится маленький, радиус которого в 10 раз меньше. Воздух снаружи откачивают, после чего радиус большого пузыря увеличивается в 2 раза. Во сколько раз увеличится радиус внутреннего пузыря? Температуру считайте постоянной, влиянием силы тяжести можно пренебречь.
Подробнее
Задача по физике – 12678
В теплоизолированном цилиндрическом сосуде под поршнем находится сильно разреженный гелий при температуре $T_{0} = 100 К$. Поршень очень медленно отодвигают на некоторое расстояние, после чего в сосуде устанавливается температура $T_{1} = 99 К$. Какая температура установится в сосуде, если поршень передвинуть очень быстро? Что такое “очень быстро” в этом случае? Сделайте оценку такой скорости передвижения поршня, при которой изменение температуры составит $Delta T = 0,5 К$.
Подробнее
Задача по физике – 12694
В цилиндрическом сосуде под тяжелым поршнем находится кислород (рис.). Поршень поднимают на высоту $h$ от положения равновесия, дожидаются установления температуры, затем сосуд теплоизолируют и поршень отпускают. На каком расстоянии от прежнего положения равновесия установится поршень, когда система вновь придет в равновесие? Теплоемкостью стенок и поршня пренебречь.

Подробнее
Задача по физике – 12698
Один из спаев термопары находится в комнате при температуре $t_{1} = 27^{ circ} С$, а второй – в теплоизолированном сосуде со льдом, имеющим температуру $t_{2} = 0^{ circ} C$ (см. рисунок). Мощность, развиваемая термопарой, выделяется на сопротивлении нагревателя, который помещен в другой теплоизолированный сосуд, содержащий воду. Оцените, на сколько повысится температура воды к моменту окончания плавления льда. Считайте, что все сопротивление цепи сосредоточено в нагревателе. Массы воды и льда одинаковы. Удельная теплоемкость воды $c = – 4,2 кДж/(кг cdot К)$, удельная теплота плавления льда $lambda = 335 кДж/кг$.

Подробнее
Задача по физике – 12704
Два сосуда объемом $V = 0,5 л$ каждый соединены вертикальной стеклянной трубкой сечением $S = 1 см^{2}$ (рас.). Трубка перекрыта подвижным поршнем – магнитом массой $m = 2,0 г$, который может двигаться вдоль трубки без трения. При помощи катушек, подключенных к генератору переменною напряжения, возбуждают колебания поршня вдоль трубки. На рисунке приведена экспериментально полученная зависимость амплитуды установившихся колебаний поршня от частоты приложенного переменного напряжения. Определите по этим данным отношение молярных теплоемкостей $C_{p}/C_{V}$ для воздуха. В первом опыте вентиль наверху был закрыт. При какой частоте наступит максимум при открытом вентиле? Оцените амплитуду колебаний поршня в этом случае на частоте $f_{0}$. Давление воздуха $p_{0} = 1 атм.


Подробнее
Задача по физике – 12705
Пленка при температуре $t_{1}= + 50^{ circ} С$ имеет коэффициент поверхностного натяжения $sigma_{1} = 0,020 Н/м$. После увеличения температуры до $t_{2} = +51^{ circ} С$ коэффициент поверхностного натяжения падает до $sigma_{2} = 0,0195 Н/м$. Будем медленно растягивать пленку так, чтобы ее температура оставалась постоянной. Поглощает пленка при этом тепло из окружающей среды или, наоборот, отдает его? Оцените количественно этот теплообмен при растяжении пленки от $S_{1} = 1 м^{2}$ до $S_{2} = 1,5 м^{2}$ при температуре $+ 50^{ circ} C$.
Указание. Подумайте, как применить тут формулу для КПД цикла Карно.

Подробнее
Задача по физике – 12710
Возьмем короткую трубочку небольшого диаметра $D$ и выдуем мыльный пузырь радиусом $R_{0} gg D$. Откроем теперь конец трубочки и подождем, пока пузырь сдуется. Оцените время жизни такого пузыря от начала сдувания, если $D = 2 мм, R_{0} = 2 см$. Коэффициент поверхностного натяжения воды $sigma = 0,07 Н/м$.
Подробнее
Задача по физике – 12714
В насыщенные пары воды при температуре $t = 100^{ circ} С$ поместили металлическую пластину, охлажденную до температуры жидкого азота. Оцените начальную скорость роста толщины слоя намерзающего льда.
Подробнее
Задача по физике – 12719
В объеме $V_{0}$ при температуре $T_{0}$ и давлении $p$ находился воздух, содержащий некоторое количество озона $O_{3}$. После долгого выдерживания в тени озон полностью превратился в молекулярный кислород. При том же давлении температура воздуха стала $T$, объем – $V$. Найдите начальное число молей озона.
Подробнее
Задача по физике – 12728
Сосуд объемом $V = 10 л$ с площадью поперечного сечения $S = 0,01 м^{2}$ разделен пополам тяжелым поршнем массой $m = 1 кг$, который может двигаться без трения. В каждой половине сосуда содержится $m = 5 г$ воды, а воздух откачан. Температура сосуда и его содержимом поддерживается равной $T = 350 К$. Поршень сдвигают от середины на расстояние $d = 1 см$ и отпускают. Как будет двигаться поршень? Как зависит характер движения поршня от температуры сосуда?
Подробнее
Задача по физике – 12729
В сосуде под поршнем находится некоторое количество азота. Медленно отодвигая поршень, плавно уменьшим давление газа. Какова молярная теплоемкость газа на малом участке процесса, если при увеличении объема па 1% давление уменьшилось на 0,5%?
Подробнее
Задача по физике – 12730
Газовая смесь состоит из равного числа молей гелия, азота и углекислого газа. Найдите показатель адиабаты для такого газа.
Подробнее
Источник
1. На рисунке представлен график зависимости температуры t от времени τ для куска льда массой 480 г, помещённого при температуре −20 °С в калориметр. В тот же калориметр помещён нагреватель. Найдите, какую мощность развивал нагреватель при плавлении льда, считая эту мощность в течение всего процесса постоянной. Теплоёмкостью калориметра и нагревателя можно пренебречь. (Удельная теплота плавления льда — 330 кДж/кг.)
Решение.
Чтобы расплавить весь имеющийся лёд необходимо затратить энергию:
Здесь m — масса льда, λ — удельная теплота плавления льда.
Мощность нагревателя W — есть расход энергии в единицу времени. Время плавления определяем по графику:
Тогда, используя табличные данные и данные задачи, получаем:
Ответ: 330 Вт.
2. Сколько граммов воды можно нагреть на спиртовке на 30 °С, если сжечь в ней 21 грамм спирта? КПД спиртовки (с учётом потерь теплоты) равен 30 %. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 30 %, получаем:
Ответ: 1450 г.
3. Теплоизолированный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 40 г, а масса воды 600 г. В сосуд впускают водяной пар при температуре +100 °С. Найдите массу впущенного пара, если известно, что окончательная температура, установившаяся в сосуде, равна +20 °С.
Решение.
Окончательная температура положительна, значит, весь лед расплавился, и вся получившаяся вода нагрелась.
При этом пар конденсировался и полученная вода остыла. С учетом этого запишем уравнение теплового баланса:
и выразим отсюда массу пара:
Здесь Qпол и Qотд — полученная и отданная теплота соответственно, m1, m2, m3 — массы льда, воды, пара соответственно, λ — удельная теплота плавления льда, c — удельная теплоемкость воды, τ — удельная теплота парообразования, t2 — конечная температура, t1 — исходная температура смеси лед-вода, t3 — температура пара.
Переведя граммы в килограммы и подставляя данные задачи и табличные данные, получаем:
Ответ: 25,4 г.
4. Литровую кастрюлю, полностью заполненную водой, из комнаты вынесли на мороз. Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда?
Примечание.
Удельную теплоту плавления льда считать равной
Решение.
Поскольку объём воды равен одному литру, масса воды равна одному килограмму. Таким образом, кристаллизовался 1 кг льда, выделив при этом
Также тепло выделялось при охлаждении льда:
Следовательно, при кристаллизации и охлаждении льда выделилось 372 кДж энергии.
Ответ: 372 кДж.
5. Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С? КПД спиртовки (с учётом потерь теплоты) равен 20%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 20%, получаем:
Ответ: 33,6 г.
6. Какое количество теплоты выделится при кристаллизации 2 кг расплавленного олова, взятого при температуре кристаллизации, и последующем его охлаждении до 32 °С? (Удельная теплоёмкость олова — 230 Дж/(кг · °С).)
7. Тонкостенный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 350 г, а масса воды 550 г. Сосуд начинают нагревать на горелке мощностью 1,5 кВт. Сколько времени понадобится, чтобы довести содержимое сосуда до кипения? Потерями теплоты и удельной теплоёмкостью сосуда, а также испарением воды можно пренебречь.
Решение.
Чтобы довести содержимое сосуда до кипения за время τ, необходимо расплавить лёд, а затем нагреть всю получившуюся воду до температуры кипения, следовательно, затратить энергию, равную
Здесь m1, m2, — массы льда и воды соответственно, λ — удельная теплота плавления льда, c — удельная теплоёмкость воды, t2 — температура кипения воды, t1 — исходная температура смеси лед-вода.
Мощность горелки W есть расход энергии в единицу времени, откуда находим τ:
Подставляя табличные данные и данные задачи, находим:
Ответ: 5,5 мин.
8. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 1 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоёмкость вещества в твёрдом состоянии.
Решение.
Удельная теплоёмкость — это количество теплоты, необходимое для того, чтобы нагреть вещество на 1 °C. Из графика видно, что для нагревания 1 кг вещества на 200 °C потребовалось 50 кДж. Таким образом, удельная теплоёмкость равна:
Ответ:
9. В тонкостенный сосуд налили воду, поставили его на электрическую плитку мощностью 800 Вт и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите массу налитой в сосуд воды. Потерями теплоты и теплоёмкостью сосуда пренебречь.
10. Какое количество теплоты потребуется, чтобы в алюминиевом чайнике массой 700 г вскипятить 2 кг воды? Первоначально чайник с водой имели температуру 20 °С.
Примечание.
Удельную теплоёмкость алюминия считать равной
Решение.
Для нагревания чайника необходимо
Для нагревания воды:
Всего потребуется
Ответ: 723,52 кДж.
11. Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении?
Решение.
В данном случае тепло отдавали пар и получившаяся из него вода. Пар отдал:
вода отдала:
Таким образом:
Ответ: 5104 кДж.
12. Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь.
Решение.
Для нагревания льда до температуры плавления необходимо:
Для превращения льда в воду:
Таким образом:
Ответ: 175 500 Дж.
13. В сосуд с водой положили кусок льда. Каково отношение массы льда к массе воды, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальные температуры воды и льда определите из графика зависимости температуры t от времени τ для воды и льда в процессе теплообмена.
Решение.
Лёд растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 0,42.
14. Как изменится внутренняя энергия 500 г воды, взятой при 20°С, при её превращении в лёд при температуре 0 °С?
Решение.
При охлаждении воды до 0 °С выделится количество теплоты, равное:
Затем при кристаллизации воды выделится количество теплоты, равное:
Таким образом, всего вода отдаст теплоты.
Ответ: 207 кДж.
15. В стакан массой 100 г, долго стоявший на улице, налили 200 г воды из лужи при температуре +10 °С и опустили в неё кипятильник. Через 5 минут работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите мощность кипятильника. Удельная теплоёмкость материала стакана равна 600 Дж/(кг · °С).
16. Два однородных кубика привели в тепловой контакт друг с другом (см. рисунок). Первый кубик изготовлен из цинка, длина его ребра 2 см, а начальная температура t1 = 1 °C. Второй кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t2 = 74,2 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности цинка и меди соответственно:
Удельные теплоёмкости цинка и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Заметим, что теплоёмкости цинка и меди равны, поэтому их можно сократить. Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
17. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
Решение.
Плотность воды равна 1 кг/л, теплоемкость равна 4 200 Дж/кг. Таким образом, изначально мы имеем
