Как найти высоту сосуда формула

Определение

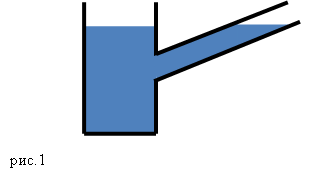
Соединенные между собой сосуды называют сообщающимися.

В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.

Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:

[p=rho gh left(1right),]

где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.

Жидкости разной плотности в сообщающихся сосудах

Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).

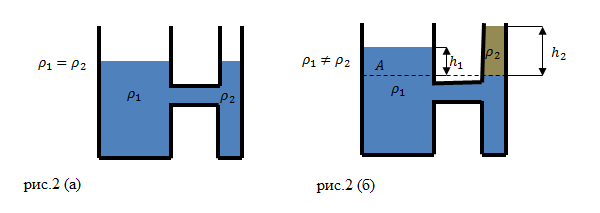
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:

[{rho }_1gh_1={rho }_2gh_2left(2right),]

где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:

[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]

Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.

Гидравлический пресс и другие примеры использования сообщающихся сосудов

В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.

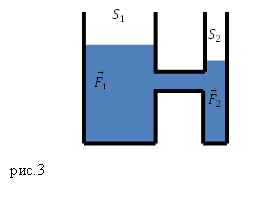
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:

[p_1=frac{F_1}{S_1}left(4right).]

Второй поршень давит на жидкость:

[p_2=frac{F_2}{S_2}left(5right).]

Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:

[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]

Получим:

[F_1=F_2frac{S_1}{S_2}(7)]

величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.

По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.

Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.

Примеры задач с решением

Пример 1

Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.

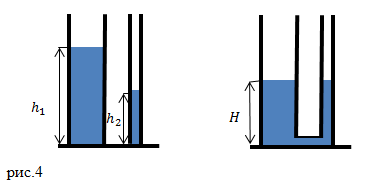
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:

[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]

где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:

[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]

где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:

[Delta V_1=Delta V_2left(1.3right).]

Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:

[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]

Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:

[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=] [=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]

Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$

Пример 2

Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?

Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):

[F_1=F_2frac{S_1}{S_2}(2.1)]

Ответ. $F_1=F_2frac{S_1}{S_2}$

Читать дальше: условия плавания тел.

Источник

4.2. Элементы гидростатики

4.2.5. Сообщающиеся сосуды

Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.

Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:

h 1 h 2 = ρ 2 ρ 1 ,

где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.

Указанный закон справедлив в отсутствие сил поверхностного натяжения.

Если сообщающиеся сосуды заполнены однородной жидкостью

ρ1 = ρ2,

то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):

h1 = h2,

где h1 – высота столба жидкости в левом колене; h2 – высота столба жидкости в правом колене сообщающихся сосудов.

Рис. 4.14

Если сообщающиеся сосуды заполнены разнородными жидкостями

ρ1 ≠ ρ2,

то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение

h 1 h 2 = ρ 2 ρ 1 ,

где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.

Рис. 4.15

Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой

p1 = ρ1gh1,

в правом колене –

p2 = ρ2gh2 + ρ3gh3.

Рис. 4.16

Равенство давлений на указанном уровне

p1 = p2

позволяет записать тождество:

ρ1h1 = ρ2h2 + ρ3h3.

Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.

Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.

Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:

• в первом сосуде оказывается масса жидкости

m1 = ρV1 = ρ∆h1S1,

где ρ – плотность жидкости; V1 = S1∆h1 – объем жидкости в первом сосуде; S1 – площадь поперечного сечения первого сосуда; ∆h1 – повышение уровня жидкости в первом сосуде;

• во втором сосуде оказывается масса жидкости

m2 = ρV2 = ρ∆h2S2,

где V2 = S2∆h2 – объем жидкости во втором сосуде; S2 – площадь поперечного сечения второго сосуда; ∆h2 – повышение уровня жидкости во втором сосуде.

Повышение уровней жидкости в обоих сосудах одинаково:

∆h1 = ∆h2 = ∆h,

поэтому масса жидкости, добавленной в систему, определяется формулой

m = m1 + m2 = ρ∆h(S1 + S2).

Выразим отсюда искомое значение ∆h:

Δ h = m ρ ( S 1 + S 2 ) .

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для первого (широкого) сосуда

S 1 = π d 1 2 4 ,

• для второго (узкого) сосуда

S 2 = π d 2 2 4 ,

где d1 = 2d2 – диаметр первого (широкого) сосуда; d2 – диаметр второго (узкого) сосуда.

Отношение площадей

S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4

позволяет найти площадь широкого сосуда:

S1 = 4S2.

Подставив S1 в формулу для ∆h

Δ h = m ρ ( 4 S 2 + S 2 ) = m 5 ρ S 2 ,

рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:

Δ h = 0,12 5 ⋅ 1,6 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 15 ⋅ 10 − 3 м = 15 мм.

Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем – 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.

Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:

p1 = p2,

где p1 – давление в широком сосуде; p2 – давление в узком сосуде.

На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.

Гидростатическое давление на выбранном уровне:

• в широком сосуде

p1 = ρ1gh1,

где ρ1 – плотность жидкости, заполняющей систему изначально; g – модуль ускорения свободного падения; h1 – высота столба жидкости в широком сосуде;

• в узком сосуде

p2 = ρ2gh2 + ρ3gh3,

где ρ2 – плотность первой жидкости, добавленной в узкий сосуд; h2 – высота столба первой жидкости; ρ3 – плотность второй жидкости, добавленной в узкий сосуд; h3 – высота столба второй жидкости.

Равенство давлений на указанном уровне

ρ1gh1 = ρ2gh2 + ρ3gh3

позволяет определить высоту столба жидкости в широком сосуде:

h 1 = 1 ρ 1 ( ρ 2 h 2 + ρ 3 h 3 ) ,

где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:

• для первой жидкости

h 2 = m 2 ρ 2 S 2 ;

• для второй жидкости

h 3 = m 3 ρ 3 S 2 ,

где S2 – площадь поперечного сечения узкого сосуда; m2 – масса первой жидкости, добавленной в узкий сосуд; m3 – масса второй жидкости, добавленной в узкий сосуд.

Подстановка h2 и h3 в формулу для h1 дает

h 1 = 1 ρ 1 ( ρ 2 m 2 ρ 2 S 2 + ρ 3 m 3 ρ 3 S 2 ) = m 2 + m 3 ρ 1 S 2 .

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для широкого сосуда

S 1 = π d 1 2 4 ,

• для узкого сосуда

S 2 = π d 2 2 4 ,

где d1 = 2d2 – диаметр широкого сосуда; d2 – диаметр узкого сосуда.

Отношение площадей

S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4

позволяет найти площадь узкого сосуда:

S 2 = S 1 4 .

Таким образом, высота столба жидкости в широком сосуде определяется выражением

h 1 = 4 ( m 2 + m 3 ) ρ 1 S 1 .

Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:

h 2 + h 3 = m 2 ρ 2 S 2 + m 3 ρ 3 S 2 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) .

Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле

Δ h = ( h 2 + h 3 ) − h 1 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) − 4 ( m 2 + m 3 ) ρ 1 S 1 =

= 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 − ( m 2 + m 3 ) ρ 1 ) .

Произведем вычисление:

Δ h = 4 10 ⋅ 10 − 4 ( 0,12 2,0 ⋅ 10 3 + 0,12 4,0 ⋅ 10 3 − 0,12 + 0,12 6,0 ⋅ 10 3 ) = 0,20 м = 20 см.

Источник