Как найти высоту жидкости в сосуде формула
Давление
«Давление». Значит, что-то на что-то давит. То есть воздействует. Хм… Кажется, у нас уже была физическая величина, которая показывала, как интенсивно что-то действует на что-то другое. Какая это величина, как вы думаете?
Какая величина описывает интенсивность действия одного тела на другое?
Работа.
Сила.
Импульс.
Кинетическая энергия.
Давление. «Опять новая величина? А что, тех величин, которые уже есть, недостаточно? – резонно можете спросить вы. – У нас есть понятие силы для того, чтобы описывать, как и что действует на некоторое тело. Зачем ещё и давление?» Понять, зачем нужно давление, вам поможет следующий пример.
Представьте себе ситуацию: есть 101010 человек, и на них сверху опускают тяжеленную коробку массой в 500500500 килограмм.
Смогут ли они удержать такую коробку? Смогут. Почему?
Почему десять человек смогут удержать коробку массой 500500500 кг?
Потому что они сильны духом.
Потому что с ними бог.
Потому что на одного человека приходится небольшая масса в 505050 кг.
Потому что 500500500 кг легко удержит и один человек.
А смог ли бы удержать коробку массой 500500500 кг один человек? Нет, скорее всего – она бы его раздавила.
Отсюда мы можем сделать вывод, что имеет значение не только масса тела, не только сила тяжести тела, не только интенсивность воздействия – то есть сила FFF – но и то, как распределяется эта нагрузка. Если сила действует на некоторое тело, которое имеет некоторый размер, то логично, что будет иметь значение, на какую площадь SSS воздействует эта нагрузка.
Давление – величина, которая учитывает распределение воздействия некоторой силы FFF на некоторую площадь SSS.
Как вы думаете, как будет правильно в таком случае записать формулу для давления ppp? Выберите правильный вариант.
p=F−Sp = F – Sp=F−S.
p=FSp = frac{F}{S}p=SF.
p=SFp = frac{S}{F}p=FS.
p=FSp = FS p=FS.
Итак, запишем формулу давления:
p=FSp=frac{F}{S}p=SF.
Стоит отметить, что площадь SSS, которая входит в формулу давления, – это площадь соприкосновения предмета, «который давит», и предмета, «на который давят». Например, если человек идет по поверхности льда пруда площадью 400400400 кв. м., то в формулу давления, которое человек оказывает на лед, надо подставить площадь подошв его ботинок, а не всей поверхности пруда целиком.
Единица измерения давления – Паскаль:
[p]=[FS]=Ньютонметр2=Паскаль=Па [p] = [ frac{F}{S} ] =frac{Ньютон}{метр^2}= Паскаль = Па[p]=[SF]=метр2Ньютон=Паскаль=Па.
Разберем задачу.
Условие
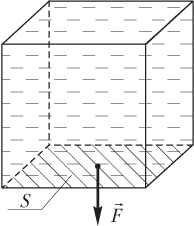
Аквариум, изображённый на рисунке, доверху наполнили водой. Найдите давление воды на дно аквариума. Плотность воды равна ρrhoρ. Атмосферное давление не учитывать.
- ρgarho gaρga
- 2ρga32 rho g a^3 2ρga3
- Pg2a2frac{Pg}{2a^2}2a2Pg
- 2ρga2 rho ga 2ρga
(Источник: ЕГЭ-2013. Физика. Реальный экзамен. Урал. Вариант 1)
Решение
Шаг 1. Вспомним формулу давления.
Выберите правильную формулу для давления.
p=F−Sp = F – Sp=F−S
p=FSp = frac{F}{S}p=SF
p=SFp = frac{S}{F}p=FS
p=FSp = FS p=FS
Шаг 2. Определим, какая сила давит на дно сосуда.
Какая сила давит на дно сосуда?
сила тяжести воды
сила реакции опоры сосуда
сила трения воды о стенки сосуда
сила вязкого внутреннего трения жидкости
Шаг 3. Попробуем выразить силу тяжести через известные нам величины. Для начала просто запишем формулу силу тяжести.
Как можно вычислить силу тяжести воды?
F=mghF = mghF=mgh
F=mgF = mgF=mg
F=mgSF = frac{mg}{S}F=Smg
F=mgSF = mgSF=mgS
Шаг 4. В формуле F=mgF=mgF=mg нам неизвестна масса воды mmm. Ее можно выразить через другие величины, данные в условии.
Как можно вычислить силу тяжести, зная размеры сосуда и плотность?
F=mg=4ρa3gF = mg = 4 rho a^3 g F=mg=4ρa3g
F=mg=2ρagF = mg = 2 rho ag F=mg=2ρag
F=mg=ρagF = mg = rho ag F=mg=ρag
F=mg=ρgF = mg = rho g F=mg=ρg
Шаг 5. Вычислим давление по формуле p=FSp = frac{F}{S}p=SF.
Подставим в формулу давления ранее полученное выражение для силы:
p=FS=4ρa3g2a⋅a=2ρagp = frac{F}{S} = frac{4 rho a^3 g}{2a cdot a} = 2 rho agp=SF=2a⋅a4ρa3g=2ρag.
Правильный ответ: 4) 2ρga2 rho ga2ρga.
Давление столба жидкости
Представьте, что вы опустились со специальным аквалангом на дно озера.
Если вы поднимите голову вверх, то увидите, что над вами находится толща воды. Целый водяной столб. И он находится прямо над вами.
Как вы думаете, что он делает с вами?
Ничего не делает.
Выталкивает меня наверх.
Давит на меня.
Пытается сместить меня вбок.
На столб действует сила тяжести: F=mgF = mgF=mg.
Если площадь человека в поперечине равна SSS, то на человека будет оказываться давление: p=FS=mgSp = frac{F}{S} = frac{mg}{S} p=SF=Smg.
Массу жидкости можно расписать.
Как правильно расписать массу жидкости?
m=ρVm = rho Vm=ρV
m=ρVm = frac{rho}{V}m=Vρ
m=Vρm = frac{V}{rho}m=ρV
m=ρ+Vm = rho + Vm=ρ+V
Если представить, что столб жидкости – цилиндр высотой hhh и площадью поперечного сечения SSS, то его объём можно выразить через hhh и SSS.
Как можно записать объем столба жидкости? Выберите правильную формулу.
V=hSV = frac{h}{S}V=Sh
V=hSV = hS V=hS
V=h+SV = h + S V=h+S
V=ShV = frac{S}{h} V=hS
Тогда давление столба жидкости можно записать следующим образом: p=FS=mgS=ρhSgS=ρghp = frac{F}{S} = frac{mg}{S} = frac{rho hSg}{S} = rho gh p=SF=Smg=SρhSg=ρgh.
Итак, гидростатическое давление столба жидкости на глубине hhh рассчитывается по формуле p=ρgh.p = rho gh {.}p=ρgh.
Решим задачу.
Сосуд, изображённый на рисунке, доверху наполнили некоторой жидкостью. Найдите давление жидкости на дно сосуда. Плотность жидкости равна ρrhoρ. Атмосферное давление не учитывать.
(Источник: ЕГЭ-2013. Физика. Урал. Вариант 6)
2ρga32 rho g a^3 2ρga3
2ρga2 rho g a 2ρga
2ρga22 rho g a^2 2ρga2
ρga rho g a ρga
Гидростатика. Закон Паскаля
Раздел гидростатики в физике занимается давлениями неподвижных жидкостей. Нечто похожее у нас уже было в разделе «Статика», когда мы рассматривали неподвижность твёрдых тел, рассматривали правило моментов: чтобы вращающие моменты уравновешивали друг друга.
В гидростатике – нечто похожее: рассматриваются давления жидкости в условии, когда она неподвижна – то есть не течёт. Для этого раздела важен закон Паскаля:
Давление жидкости передаётся в любую точку без изменения во всех направлениях.
Сложная формулировка. Сложный закон. Понять его можно на примере. Возьмём полиэтиленовый пакет, нальём в него жидкость и сделаем несколько небольших дырочек. Будем давить сверху на этот пакет с жидкостью. Что мы увидим? Вода будет литься из каждой дырочки.
И можно заметить, что наше давление сверху на пакет будет передаваться без изменения в каждую «дырочку» пакета – струйки воды получатся примерно одинаковые, хоть и будут направлены в разные стороны.
Получается, что если до некоторой точки жидкости дошло давление, то давление от этой точки будет распространяться во все стороны.
На основе закона Паскаля основано действие различных гидравлических прессов и других механических устройств, в которых требуется передача давления чего-либо из одной точки – в другую точку (например – экскаватора, тормозной системы автомобилей). Такое устройство может представлять собой трубку, внутри которой находится жидкость. С одной стороны трубки – давят на жидкость, жидкость передаёт это давление – и давит на что-то с другого конца трубки.
Для того чтобы закон Паскаля стал вам окончательно понятен, приведём ещё один пример. Допустим, у нас есть палка. Просто палка. И мы давим этой палкой на землю. Действуем сверху вниз. Если земля не слишком твёрдая, то палка «уйдёт» у нас вниз. И только вниз. Ни вбок, ни вверх. Вниз.
Рассмотрим другой случай. Пусть у нас есть трубка, а на её конце – резиновый шарик. А внутри трубки и шарика – жидкость. Тогда, если мы будем давить на жидкость в трубке, то шарик у нас будет раздуваться во все стороны. Не только вниз, не только вбок – а во все стороны сразу. То есть давление в жидкости передаётся во все стороны, а давление в твёрдых телах – преимущественно в том направлении, в котором приложено давление.
Разберем задачу.
Условие
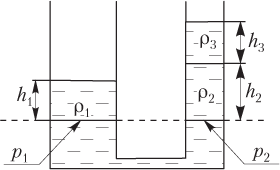
В широкую U-образную трубку с вертикальными прямыми коленами налиты неизвестная жидкость плотностью ρ1rho _1 ρ1 и вода плотностью ρ2=1,0⋅103 кг/м3rho _2 = 1,0 cdot 10^3text{ }кг/м^3 ρ2=1,0⋅103 кг/м3 (см. рисунок).
На рисунке b=10b = 10b=10 см, h=24h = 24h=24 см, H=30H = 30H=30 см. Чему равна плотность ρ1rho _1ρ1?
- 0,6⋅103 кг/м30,6cdot 10^3text{ }кг/м^30,6⋅103 кг/м3
- 0,7⋅103 кг/м30,7cdot 10^3text{ }кг/м^30,7⋅103 кг/м3
- 0,8⋅103 кг/м30,8cdot 10^3text{ }кг/м^30,8⋅103 кг/м3
- 0,9⋅103 кг/м30,9cdot 10^3text{ }кг/м^30,9⋅103 кг/м3
(Источник: сайт решуегэ.рф)
Решение
Шаг 1. В задаче даны плотности и высоты столбов жидкости. Определим тип этой задачи.
Как вы думаете, на что может быть эта задача?
на силы
на гидростатическое давление жидкостей
на уравнение моментов сил
на объёмы
Шаг 2. Так же, как в задачах на правило моментов вращающие моменты уравновешивают друг друга, в задачах на гидростатическое давление мы часто будем иметь дело с противодействием.
Кто кому в этой задаче противодействует?
Жидкости в левой части трубки противодействуют жидкости в правой части трубки.
Жидкость плотностью ρ1rho _1ρ1 противодействует жидкости плотностью ρ2rho _2ρ2.
Сила тяжести противодействует силе давления жидкости.
U-образная рубка противодействует жидкости.
Шаг 3. Определим, что оказывает давление в левой части трубки.
Что давит в левой части трубки?
жидкость ρ1rho _1ρ1 и небольшая часть жидкости ρ2rho _2ρ2
жидкость ρ1rho _1ρ1
жидкость ρ2rho _2ρ2
материал трубки
Шаг 4. Запишем условие равенства гидростатических давлений.
Как правильно записать условие равенства гидростатических давлений?
ρ1gH+ρ2gb=ρ2ghrho _1 gH + rho _2 gb = rho _2 ghρ1gH+ρ2gb=ρ2gh
ρ1g(H−b)+ρ2gb=ρ2ghrho _1 g(H – b) + rho _2 gb = rho _2 ghρ1g(H−b)+ρ2gb=ρ2gh
ρ1gH=ρ2gh+ρ2gbrho _1 gH = rho _2 gh + rho _2 gbρ1gH=ρ2gh+ρ2gb
ρ1g(H−b)=ρ2gh+ρ2gbrho _1 g(H – b) = rho _2 gh + rho _2 gbρ1g(H−b)=ρ2gh+ρ2gb
Шаг 5. Преобразуем выражение и подставим численные значения.
Для начала заметим, что можно сократить всё выражение на ускорение свободного падения ggg:
ρ1g(H−b)+ρ2gb=ρ2gh⇔ρ1(H−b)+ρ2b=ρ2hrho _1 g(H – b) + rho _2 gb = rho _2 ghLeftrightarrowrho _1(H – b) + rho _2 b = rho _2 hρ1g(H−b)+ρ2gb=ρ2gh⇔ρ1(H−b)+ρ2b=ρ2h.
В задаче просят найти плотность жидкости ρ1rho _1ρ1.
Сделаем это:
ρ1=ρ2h−ρ2bH−b=ρ2(h−b)H−b=ρ2h−bH−brho _1 = frac{rho _2 h – rho _2 b}{H – b} = frac{rho _2 (h – b)}{H – b} = rho _2 frac{h – b}{H – b}ρ1=H−bρ2h−ρ2b=H−bρ2(h−b)=ρ2H−bh−b.
Подставим численные значения:
ρ1=ρ2h−bH−b=1⋅103кгм3⋅24см−10см30см−10см=rho _1 = rho _2 frac{h – b}{H – b} = 1 cdot 10^3 frac{кг}{м^3} cdot frac{24 см – 10 см}{30 см – 10 см} =ρ1=ρ2H−bh−b=1⋅103м3кг⋅30см−10см24см−10см=
=103кгм3⋅0,7=700кгм3= 10^3 frac{кг}{м^3} cdot 0,7 = 700 frac{кг}{м^3}=103м3кг⋅0,7=700м3кг.
Правильный ответ: 2) 0,7⋅103 кг/м30,7 cdot 10^3text{ }кг/м^30,7⋅103 кг/м3.
Источник
4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр — гидростатическое давление на дно сосуда; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Рис. 4.10
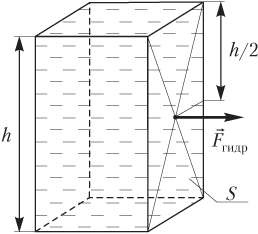
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
Fгидр=pгидрS=ρ0gh2S,
где pгидр — гидростатическое давление на дно сосуда; ρж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S — площадь дна водоема.
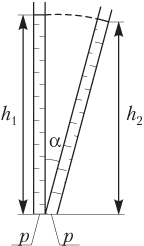
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h1 — высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
〈Fгидр〉=〈p〉S,
где 〈p〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
〈p〉=ρ0gh2,
где ρ0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈p〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈Fгидр〉=πρ0gRh2.
Расчет дает значение:
〈Fгидр〉=π⋅2,5⋅103⋅10⋅10⋅10−2⋅(30⋅10−2)2≈707 Н≈0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h=3pатмρ0g
и произведем вычисление:
h=3⋅100⋅1031,0⋅103⋅10=30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
4.2. Элементы гидростатики
4.2.5. Сообщающиеся сосуды
Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.
Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Указанный закон справедлив в отсутствие сил поверхностного натяжения.
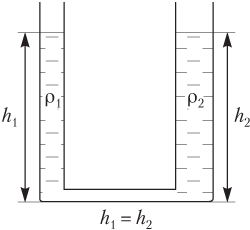
Если сообщающиеся сосуды заполнены однородной жидкостью
ρ1 = ρ2,
то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):
h1 = h2,
где h1 — высота столба жидкости в левом колене; h2 — высота столба жидкости в правом колене сообщающихся сосудов.
Рис. 4.14
Если сообщающиеся сосуды заполнены разнородными жидкостями
ρ1 ≠ ρ2,
то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Рис. 4.15
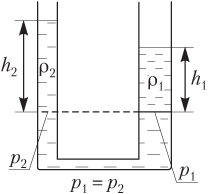
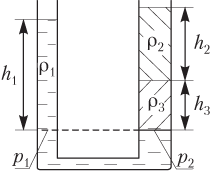
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой
p1 = ρ1gh1,
в правом колене —
p2 = ρ2gh2 + ρ3gh3.
Рис. 4.16
Равенство давлений на указанном уровне
p1 = p2
позволяет записать тождество:
ρ1h1 = ρ2h2 + ρ3h3.
Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.
Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:
- в первом сосуде оказывается масса жидкости
m1 = ρV1 = ρ∆h1S1,
где ρ — плотность жидкости; V1 = S1∆h1 — объем жидкости в первом сосуде; S1 — площадь поперечного сечения первого сосуда; ∆h1 — повышение уровня жидкости в первом сосуде;
- во втором сосуде оказывается масса жидкости
m2 = ρV2 = ρ∆h2S2,
где V2 = S2∆h2 — объем жидкости во втором сосуде; S2 — площадь поперечного сечения второго сосуда; ∆h2 — повышение уровня жидкости во втором сосуде.
Повышение уровней жидкости в обоих сосудах одинаково:
∆h1 = ∆h2 = ∆h,
поэтому масса жидкости, добавленной в систему, определяется формулой
m = m1 + m2 = ρ∆h(S1 + S2).
Выразим отсюда искомое значение ∆h:
Δh=mρ(S1+S2).
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для первого (широкого) сосуда
S1=πd124,
- для второго (узкого) сосуда
S2=πd224,
где d1 = 2d2 — диаметр первого (широкого) сосуда; d2 — диаметр второго (узкого) сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь широкого сосуда:
S1 = 4S2.
Подставив S1 в формулу для ∆h
Δh=mρ(4S2+S2)=m5ρS2,
рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:
Δh=0,125⋅1,6⋅103⋅10⋅10−4=15⋅10−3 м=15 мм.
Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем — 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:
p1 = p2,
где p1 — давление в широком сосуде; p2 — давление в узком сосуде.
На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.
Гидростатическое давление на выбранном уровне:
- в широком сосуде
p1 = ρ1gh1,
где ρ1 — плотность жидкости, заполняющей систему изначально; g — модуль ускорения свободного падения; h1 — высота столба жидкости в широком сосуде;
- в узком сосуде
p2 = ρ2gh2 + ρ3gh3,
где ρ2 — плотность первой жидкости, добавленной в узкий сосуд; h2 — высота столба первой жидкости; ρ3 — плотность второй жидкости, добавленной в узкий сосуд; h3 — высота столба второй жидкости.
Равенство давлений на указанном уровне
ρ1gh1 = ρ2gh2 + ρ3gh3
позволяет определить высоту столба жидкости в широком сосуде:
h1=1ρ1(ρ2h2+ρ3h3),
где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:
- для первой жидкости
h2=m2ρ2S2;
- для второй жидкости
h3=m3ρ3S2,
где S2 — площадь поперечного сечения узкого сосуда; m2 — масса первой жидкости, добавленной в узкий сосуд; m3 — масса второй жидкости, добавленной в узкий сосуд.
Подстановка h2 и h3 в формулу для h1 дает
h1=1ρ1(ρ2m2ρ2S2+ρ3m3ρ3S2)=m2+m3ρ1S2.
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для широкого сосуда
S1=πd124,
- для узкого сосуда
S2=πd224,
где d1 = 2d2 — диаметр широкого сосуда; d2 — диаметр узкого сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь узкого сосуда:
S2=S14.
Таким образом, высота столба жидкости в широком сосуде определяется выражением
h1=4(m2+m3)ρ1S1.
Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:
h2+h3=m2ρ2S2+m3ρ3S2=4S1(m2ρ2+m3ρ3).
Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле
Δh=(h2+h3)−h1=4S1(m2ρ2+m3ρ3)−4(m2+m3)ρ1S1=
=4S1(m2ρ2+m3ρ3−(m2+m3)ρ1).
Произведем вычисление:
Δh=410⋅10−4(0,122,0⋅103+0,124,0⋅103−0,12+0,126,0⋅103)=0,20 м=20 см.
Источник