Как перелить из одного сосуда в другой

В этой статье мы рассмотрим задачи на переливания. Эти задачи относятся к теме «проценты», но это сложные задачи, я бы отнесла их к отдельному классу задач. По сложности – вполне олимпиадные задачи, уровня город-регион, для 8 класса.
Задача 1. В сосуде было 20 литров соляной кислоты. Часть кислоты отлили, и сосуд дополнили водой. Затем отлили в 2 раза большую (чем в первый раз) часть полученной смеси и снова дополнили сосуд водой. В результате получился 28 %-й раствор кислоты. Сколько литров кислоты отлили в первый раз?
Давайте последовательно рассмотрим, что происходило, по порядку.
Пусть отлили литров кислоты. Тогда осталось литров кислоты.
Теперь в сосуд добавляют литров воды и смеси становится опять 20 л. А каков процент смеси, ее концентрация?
У нас объем 20, из этого объема – л кислоты, следовательно, концентрация смеси .
Теперь отливают л смеси. Сколько кислоты там, в этих л, содержится? А вот сколько: – концентрацию умножаем на объем. Тогда в основной емкости количество кислоты уменьшилось:
Концентрация, по условию, стала 28%, или 0,28. А концентрация – доля кислоты в общем объеме:
Так как – не подходит (не могли мы от 20 л отлить 24) то ответ – 6 л.
Ответ: 6 л.
Задача 2. В двух сосудах находилось 600 г и 150 г растворов соли различной концентрации. Из каждого сосуда взяли одновременно по граммов раствора. Взятое из первого сосуда вылили во второй, а взятое из второго – в первый. После этого концентрация растворов в обоих сосудах стала одинаковой. Найдите .
Пусть – концентрация большего по массе раствора, – меньшего по массе. Тогда в первом содержится соли г, во втором г.
Теперь забираем грамм раствора из первого, тогда в нем становится меньше соли: , забираем г из второго, в нем становится меньше соли: .
Теперь взятое из второго сосуда количество раствора и соли добавляем в первый сосуд, там становится 600 г по массе, а соли стало:
Взятое из первого сосуда количество раствора и соли добавляем во второй: по массе опять 150 г, а соли стало
По условию концентрация теперь одинакова. Концентрация – количество соли к общему объему:
Упрощаем:
Откуда
Ответ: 120 г.
Задача 3. В двух сосудах находилось 40 г и 60 г растворов соли различной концентрации. Из каждого сосуда взяли одновременно по граммов раствора. Взятое из первого сосуда вылили во второй, а взятое из второго – в первый. После этого концентрация растворов в обоих сосудах стала одинаковой. Найдите n.
Решение такое же. Пробуйте решить сами, а потом сверяйте.
Показать
Задача 4. Два сосуда равных объемов до краев заполнены раствором кислоты одинаковой концентрации. Из первого сосуда отлили 1 л раствора и долили 1 л воды. Потом эту же процедуру повторили еще раз. Из второго сосуда отлили 3 л раствора и долили 3 л воды. Потом эту же процедуру повторили еще раз. В результате концентрация кислоты в первом сосуде стала в 1,96 раз больше, чем во втором. Найдите объем сосуда (в литрах).
Так же не спеша и систематично расписываем, что происходило: пусть концентрация исходного раствора , а объем л. Тогда отливаем литр из первого, таким образом убавляем количество кислоты в нем. Сначала кислоты в сосуде было , убавили на , стало . Новая концентрация
Снова отливаем литр. Кислоты было , убавили на , стало
Новая концентрация
Теперь второй раствор.
Сначала кислоты в сосуде было , убавили на , стало . Новая концентрация
Снова отливаем 3 литра. Кислоты было , убавили на , стало
Новая концентрация
По условию, концентрация кислоты в первом сосуде стала в 1,96 раз больше, чем во втором. Тогда
Ответ: 8 л.
Источник
- Главная
- Вопросы & Ответы
- Вопрос 3520349
Энджелл
более месяца назад
Просмотров : 20
Ответов : 1
Лучший ответ:
Таня Масян
Водород легче воздуха и переливать его надо “вверх”. а кислород тяжелее воздуха, и переливать его надо “вниз”. понятно о чем я?
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Таня Масян
Звуко буквенный разбор слова ключ
более месяца назад
Смотреть ответ
Просмотров : 13
Ответов : 1
Зачетный Опарыш
Как надо разрезать квадрат на четыре равных части, чтобы из них можно было составить два квадрата?
более месяца назад
Смотреть ответ
Просмотров : 17
Ответов : 1
Суррикат Мими
38 квадратных дециметров равен квадратным см
более месяца назад
Смотреть ответ
Просмотров : 7
Ответов : 1
Васян Коваль
Помогите пожалуйста с задачей.Определить как изменяется скорость реакции,если концентрацию А увеличить в 2 раза,а концентрацию B уменьшить в 3 раза.если можно с дано и решением.
более месяца назад
Смотреть ответ
Просмотров : 8
Ответов : 1
Онтонио Веселко
СРОЧНО) Какое растение имеет сложный околоцветника)тюльпан и чеснокб)кукуруза и лилияв)картофель и яблоняг)лилия и картофель
более месяца назад
Смотреть ответ
Просмотров : 4
Ответов : 1
Источник
Другие методические материалы по теме
- Решение задач на взвешивание (определение фальшивой монеты)
Рассказываем, как в 4-5 классе решать задачи на переливание из одного сосуда в другой.
Задачи на переливание заключаются в том, что даётся два (иногда больше) сосудов разного объема, и путём манипуляций с наливанием воды в сосуды и переливанием из одного сосуда в другой надо добиться, чтобы в одном из сосудов оказался ровно заданный объём воды. Меток, указывающий объём, на сосудах нет, “на глазок” наливать нельзя.
Самый простой пример – пусть у нас есть два сосуда – 5 и 7 литров. Надо в один из сосудов налить ровно три литра воды.
Шаг 1. Наливаем в сосуд 5 л воды до краёв. Тем самым мы получаем 5 литров воды.
Шаг 2. Переливаем эту воду в сосуд 7 л. Теперь в нём 5 литров, а сосуд 5 литров пустой.
Шаг 3. Опять наливаем в сосуд 5 л. воду. В сосуде 7 л сейчас налито 5 л воды, значит есть ещё место для двух литров.
Шаг 4. Переливаем воду из сосуда 5 л в сосуд 7 л, пока он не наполнится до краёв. Те самым мы нальём в него ровно 2 л, т.к. в нём уже было 5 л, и оставалось ещё место для 2 л воды.
Раз мы из сосуда 5 л отлили 2 л, то в нём осталось 3 л. Задача решена.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Задача
Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов получить 1 л воды?
Изобразим решение на схеме. Прямоугольники означают сосуды, синий цвет – воду в сосудах. Под прямоугольниками – объём сосуда, над прямоугольником – объём воды в нём.
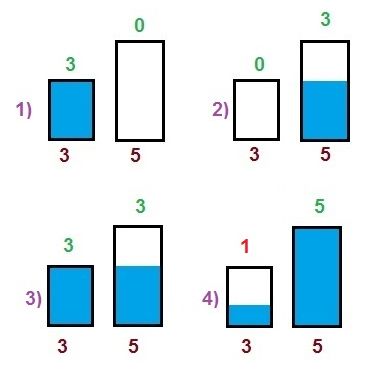
Пояснение к решению.
1 л воды можно получить, если из трёхлитрового сосуда отлить 2 литра воды. Значит нам надо добиться такой ситуации, когда в пятилитровом будем 3 литра воды, тем самым останется место ровно для двух литров, которые мы сможем перелить из трёхлитрового сосуда.
Шаг 1. Наливаем с трёхлитровый сосуд воду до краёв, получаем 3 литра воды
Шаг 2. Переливаем эту воду в пятилитровый сосуд. Теперь в нём 3 л воды, а в трёхлитровом пусто
Шаг 3. Опять наливаем в трёхлитровый сосуд воду, теперь по 3 л воды в каждом из сосудов.
Теперь мы добились той ситуации, которая нам была нужна – в пятилитровом сосуде есть место ровно для 2 л воды, а в трёхлитровом – 3 л воды.
Шаг 4. Переливаем воду из сосуда 3 л в сосуд 5 л, пока он не заполнится до краёв. Т.к. в нём было место для 2 л воды, то ровно эти 2 л и перельются, и в сосуде 3 л останется ровно 1 л. Залача решена.
Дата публикации
18.04.2020
Другие методические материалы по теме
- Решение задач на взвешивание (определение фальшивой монеты)
Купить наш видеокурс по подготовке к поступлению в 5-й класс физматшкол и участию в математических олимпиадах
Как готовиться к математическим олимпиадам и поступлению в физматшколу
Задачи раздела:
Более лёгкие задачи находятся внизу списка.
| Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить 4 л воды? Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить 4 л воды? Подробно | |
| На столе стоят десять одинаковых банок, в каждой из них по 10 монет одного достоинства, в одной банке все монеты фальшивые На столе стоят десять одинаковых банок, в каждой из них по 10 монет одного достоинства. В одной из банок все монеты фальшивые. Настоящая монета весит 10 г, а фальшивая 9 г. У вас есть весы со шкалой в граммах. Как всего лишь за одно взвешивание определить, в какой из банок находятся фальшивые монеты? Подробно | |
| Сколько взвешиваний для определения фальшивой монеты надо, если монет от 28 до 81, и от 82 до 243 Имеется набор монет одинакового достоинства, одна из которых фальшивая. Подробно | |
| Решение задач на взвешивание (определение фальшивой монеты) Рассказываем, как в 4-5 классе решать задачи на определение фальшивой монеты за минимальное число взвешиваний. Подробно |
Источник
