Как посчитать объем газа в сосуде

Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины.

Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С.

Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором.

Выберите неизвестную величину для решения уравнения состояния идеального газа:

PVTn

Абсолютное давление

P

Объем

V

Температура

T

ИЛИ

Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.

Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)

Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Определить среднюю молярную массу воздуха.

Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные:

• Выберите n (Количество в молях) в селекторе Выберите неизвестную величину.
• Введите абсолютное давление P = 100 кПа.
• Введите объем V = 1 м³.
• Введите температуру T = 0 °C.
• Нажмите кнопку Рассчитать.
• Калькулятор покажет количество молей в 1 м3 воздуха.
• Введите массу воздуха m = 1,28 кг и нажмите кнопку Рассчитать.
• Калькулятор рассчитает молярную массу воздуха M = 0,029 кг/моль

Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа.

Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:

• Выберите T (Температура) в селекторе Выберите неизвестную величину.
• Введите молярную массу кислорода N = 32 г/моль.
• Введите массу кислорода m = 128 г.
• Калькулятор рассчитает количество кислорода в молях.
• Введите объем V = 4 л и давление P = 3 МПа.
• Нажмите кнопку Рассчитать.
• Считайте температуру в кельвинах.

Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).

Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:

• Выберите T (Температура) в селекторе Выберите неизвестную величину.
• Введите давление P = 500 кПа.
• Введите температуру T = 15 °C.
• Введите объем V = 5 л.
• Нажмите кнопку Рассчитать.
• Калькулятор рассчитает количество в молях, которое будет использовано в следующем шаге.
• Выберите Объем в селекторе Выберите неизвестную величину.
• Введите температуру и давление P = 100 kPa, T = 0 °C (нормальные условия) и нажмите кнопку Рассчитать.
• Калькулятор рассчитает новый объем газа V = 23.69 л при нормальных условиях.

Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С.

Определения и формулы

Идеальный газ

Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. Идеальный газ можно представить себе в виде множества абсолютно твердых сфер, которые только сталкиваются друг с другом и больше никак не взаимодействуют.

В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния.

Закон идеального газа

Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно:

• давление (P),
• объем (V),
• количество в молях (n),
• температура (T), and
• универсальная газовая постоянная (R)

Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа:

Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении:

• P — абсолютное давление, измеряемое в СИ в паскалях (Па),
• V — объем, измеряемый в СИ в кубических метрах (м³),
• n — количество вещества (газа) в молях (сокращение моль). Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
• T — абсолютная температура.
• R — универсальная газовая постоянная, являющаяся физическим коэффициентом пропорциональности уравнения состояния идеального газа.

Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо.

Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро NA и постоянной Больцмана k:

Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона.

Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой:

Заменяя в уравнении состояния идеального газа n на m/M, имеем:

Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль

Например, молярная масса кислорода в единицах системы СИ

Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим:

Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M:

Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:

Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать

Поскольку PV/NT — постоянная величина, можно записать это иначе:

Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов.

Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными.

Закон Бойля — Мариотта (T=const, n=const)

Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными:

или

Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта.

Закон Авогадро (T=const, P=const)

Если температура и давление остаются неизменными, можно записать

Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.

Закон Гей-Люссака (P=const, n=const)

При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом.

В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).

Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const)

Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа:

Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.

Объем природного газа измеряется обычно в кубических футах¹. Поскольку газ всегда распространяется по всему объему резервуара, его количество зависит от температуры и давления. Поэтому измерения количества газа приводятся к постоянным условиям. В качестве стандартных исходных условий приняты температура 60°F и давление 30 дюймовртутного столба (приблизительно 14,73 фунт/кв. дюйм, или нормальное атмосферное давление); иногда же за эталон принимается температура 20°С (68°F). Объем газа записывается в виде величины, кратной 1000 единиц измерения, сокращенно обозначаемой буквой М; так, 3 540 000 куб. футов газа записывается как 3540 м куб. футов.

Сконструировано множество различных приборов для измерения количества (объема) газа, проходящего по трубам. Большинство замеров объема газа, извлекаемого из скважин, производится с помощью диафрагменных счетчиков-расходомеров, определяющих перепад давления между противоположными сторонами установленной в трубопроводе диафрагмы. Исходя из получаемых перепадов давления с учетом параметров диафрагмы, представляющей собой круглое отверстие в тонкой пластинке, можно рассчитать скорость истечения газа. При медленном истечении газа и давлении, близком к атмосферному, обычно применяются счетчики объемного типа. Объем газа в этих случаях определяется по числу регистрируемых счетчиком поочередных заполнений газом и освобождений от него камеры расходомера. Небольшие количества газа, увлекаемого буровым раствором и заключенного в обломках шлама, обычно улавливаются с помощью газоанализаторов.

Измерение объема газа в природном резервуаре в переводе на его объем в условиях дневной поверхности производится одним из двух распространенных методов, несколько напоминающих методы подсчета запасов нефти в природном резервуаре, с приведением их к нормальным условиям. Объемный метод, или метод насыщения, заключается в умножении объема (в акр-футах) порового пространства, заполненного газом, на отношение между пластовым давлением и давлением на поверхности в атмосферах и на температурную поправку, зависящую от того, насколько температура в природном резервуаре отличается от стандартной, равной 60°F. Коэффициент давления определяется по газо­вому закону, согласно которому объем идеального газа при постоянной температуре меняется обратно пропорционально давлению (Рисунок 1).

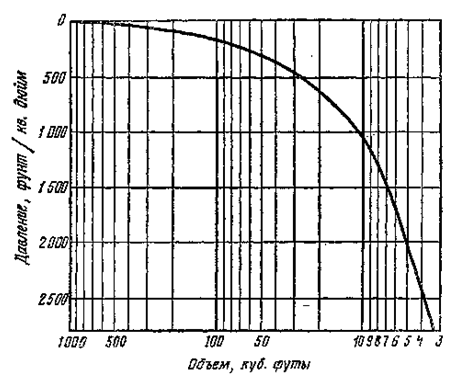
Рисунок 1: Обобщенная диаграмма изменения объема газа при повышении давления и постоянной температуре.

При атмосферном давлении, равном 14,7 фунт/кв. дюйм, для приведения объема пластового газа, находящегося под давлением 3000 фунт/кв. дюйм, к атмосферному необходимо помножить объем газа в природном резервуаре на коэффициент давления, равный:

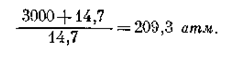Объем газа меняется также прямо пропорционально абсолютной температуре. Так, объем газа, находящегося в природном резервуаре при температуре140°F, сократится при достижении температуры дневной поверхности, равной60°F, пропорционально температурному поправочному коэффициенту, равному:

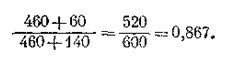Второй метод подсчета количества газа в природном резервуаре с приведением егс к условиям дневной поверхности основан на том, что при отборе газа из пласта пластовое давление снижается. Падение давления на единицу приведенного к атмосферным условиям объема газа, извлекаемого из природного резервуара, прямо пропорционально соответствующему объему газа, оставшегося в природном резервуаре. Так, например, если первоначальное пластовое давление в газовом резервуаре было 2880 фунт/кв. дюйм, а после отбора в течение нескольких лет 400 млн. куб. футов газа оно упало до 2720 фунт/кв. дюйм, то снижение давления на 100 фунт/кв. дюйм происходило с расходом газа 400 000 000/160, т.е. 2 500 000 куб. футов на единицу падения давления. Номинальный остаточный объем газа в природном резервуаре, приведенный к атмосферным условиям, будет равен тогда 2,5 млн. куб. футов, помноженным на 2720 (остаточное пластовое давление в фунтах на кв. дюйм), т.е. 6,8 млрд. куб. футов. Если принять, что пластовое давление при истощении залежи равно 250 фунт/кв. дюйм, то извлекаемые запасы газа, приведенные к условиям дневной поверхности, будут составлять 2 500 000 куб. футов × (2720-250), или 6 175 000 000 куб. футов. Применение этого метода подсчета запасов газа возможно только спустя некоторое время с начала разработки залежи.

¹В некоторых странах, особенно в СССР, объемное количество природного газа часто переводится в метрические тонны нефти; 1000 мz природного газа приравнивается к 0,824 метрической тонны нефти (обычно 1000 м3 газа считают эквивалентными 1 тнефти).