Как рассчитывается давление на стенки сосуда
Формула давления на дно и стенки сосуда
Давление жидкости обусловлено ее весом и, соответственно сила этого давления F равна весу жидкости P. Вес жидкости можно определить, зная ее массу m. А массу можно вычислить по формуле: m=ρV. Объем жидкости в прямоугольном сосуде легко рассчитать. Обозначим высоту сосуда h, а площадь дна буквой S. Тогда объем будет равен: V=Sh. Формула массы в таком случае принимает вид: m=ρV=ρSh . Вес жидкости будет равен: P=gm=gρSh. чтобы рассчитать давление, нам нужна сила этого давления. А мы уже говорили, что сила давления в данном случае равна весу жидкости, поэтому формула давления принимает следующий вид:
Формула для этого давления в атмосфере. Кроме того, поскольку давление представляет собой силу на единицу измерения площади, то. Чтобы рассчитать давление через инструмент барометра, можно было бы заменить объем ртути в барометре в уравнение. Это дало бы уравнение. Вероятно, метеоролог даст атмосферное давление или барометрическое давление в 30 дюймов. Он состоит из длинной трубки, закрытой на одном конце, заполненной ртутью и перевернутой в сосуде с ртутью. На уровне моря сила атмосферного давления будет поддерживать колонку с содержанием ртути 760 мм в высоту.
p=P/S=gρSh/S или p=gρh
То есть в итоге мы пришли к очень интересному моменту – давление не зависит от объема и формы сосуда. Оно зависит только от плотности и высоты столба конкретной жидкости в данном случае. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
Для давления газа на дно и стенки сосуда формула будет иметь точно такой же вид.
Простые приложения, связанные с давлением
Фактически вес столба ртути равен силе атмосферного давления. Подобным же образом атмосферное давление заставляет воду в подобной колонне высотой до 34 футов! После запуска атмосферное давление на поверхность верхнего контейнера заставляет воду за короткую трубу заменить воду, вытекающую из длинной трубки.
- Фактически это приводит к снижению давления воздуха внутри соломы.
- Сифон можно запустить, заполнив трубку водой.
Наблюдения Бойля можно суммировать в утверждении: при постоянной температуре объем газа изменяется обратно пропорционально давлению, оказываемому на него.
Применение давления на дно и стенки сосуда
Еще один интересный момент заключается в том, что согласно закону Паскаля давление распределяется равномерно не только на дно и стенки, но и в направлении вверх. То есть, если мы погрузим какое-либо тело на определенную глубину, то на него снизу будет действовать сила, равная силе давления на данной глубине, как бы выталкивая тело на поверхность. Именно благодаря этому явлению возможно плавание кораблей. Несмотря на довольно внушительный вес, вода выталкивает судно вследствие эффекта давления воды на стенки сосуда, которыми в данном случае являются борта корабля. С понижением глубины давление увеличивается. Люди научились использовать это явление
, делая борта кораблей в форме сужающихся вниз конусов. Именно поэтому нас доступно покорение морей и океанов.
Кинетическая молекулярная теория Пояснение
Наблюдения за давлением можно объяснить, используя следующие идеи. Быстрое движение и столкновения молекул со стенками контейнера вызывает давление. Давление пропорционально числу молекулярных столкновений и силе столкновений в определенной области. Чем больше столкновений молекул газа со стенками, тем выше давление.
В 17 веке Роберт Бойл впервые сформулировал связь между давлением, объемом и температурой, поскольку они связаны с газом по формуле. Эта формула была результатом его экспериментов с газом, и, как он заметил, газ имел тенденцию к изменению давления, когда он занимал контейнеры различного размера.
А что по поводу давления газов?
Что касается газов, то для них расчет будет абсолютно таким же. Соответственно, наибольший вес окружающего нас газа – воздуха, будет у поверхности Земли. А с увеличением высоты будет уменьшаться как среднее давление, так и плотность окружающего газа. Поэтому воздух на высоте очень разреженный. Там очень трудно как дышать, так и летать, потому что крыльям самолетов не на что опираться. Именно поэтому набирать очень большую высоту летательные аппараты могут только на очень высокой скорости, увеличивая таким образом количество воздуха под крылом в единицу времени.
Эта связь часто упоминается как Закон Бойля. Кроме того, Бойл отметил, что газы имеют тенденцию «возвращаться» к его первоначальному давлению после удаления из контейнера, в котором он либо был сжат, либо расширен. Общая разница в высоте напрямую коррелировала с давлением атмосферы.
Бойл проиллюстрировал это через формула. Рон Куртус. Давление – это сила на объекте, который распространяется по поверхности. Уравнение для давления – это сила, деленная на область, где применяется сила. Хотя это измерение является простым, когда твердое тело надавливает на твердое тело, корпус твердого тела, нажимая на жидкость или газ, требует, чтобы жидкость была ограничена в контейнере.
Нужна помощь в учебе?
Предыдущая тема: Давление в жидкости и газе
Следующая тема:   Сообщающиеся сосуды
В соответствии с законом Паскаля
гидростатическое давление на уровне
горизонтального дна сосуда при высоте
жидкости в сосуде, равной Н
,
Сила также может быть создана весом объекта. Вопросы, которые могут возникнуть, включают.
- Какое давление, когда твердое тело подталкивает другое твердое тело?
- Что происходит, когда твердое тело нажимает на ограниченную жидкость?
- Что происходит, когда сила исходит из гравитации?
Этот урок ответит на эти вопросы.
Когда вы применяете силу к твердому объекту, давление определяется как прилагаемое усилие, деленное на область применения. Вы можете видеть, что при заданной силе, если площадь поверхности меньше, давление будет больше. Если вы используете большую область, вы распространяете силу, и давление становится меньше.
Отсюда следует, что абсолютное давление
р
на горизонтальное дно не зависит
от формы сосуда и объема жидкости в нем.
При данной плотности жидкости оно
определяется лишь высотой столба
жидкостиН
и внешним давлениемр
0 .
Сила давления жидкости Р
ж на
дно сосуда зависит от его площадиF
:
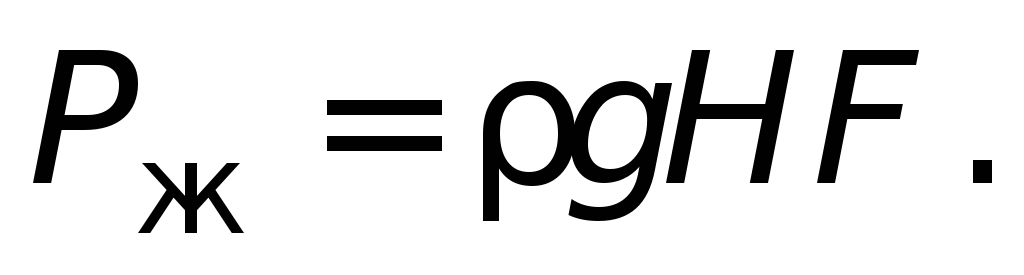 (1.8)
(1.8)
Твердое прессование на ограниченной жидкости
Когда жидкость или газ заключены в контейнер или цилиндр, вы можете создать давление, применяя усилие с помощью твердого поршня. В ограниченной жидкости – пренебрегая влиянием силы тяжести на жидкость – давление одинаково во всем контейнере, одинаково нажимая на все стенки. В случае велосипедного насоса давление, создаваемое внутри насоса, будет передаваться через шланг в велосипедную шину. Но воздух все еще ограничен.
Увеличение силы увеличит давление внутри цилиндра. Поскольку вес объекта является силой, вызванной гравитацией, мы можем заменить вес в уравнении давления. Таким образом, давление, вызванное весом объекта, – это вес, разделенный на область, где применяется вес.
Общая сила давления на дно сосуда
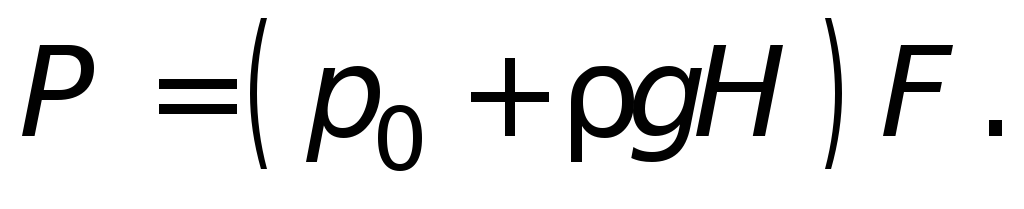 (1.9)
(1.9)
Внешнее давление р 0 передается
жидкостью каждому элементу поверхности
стенки одинаково, поэтому равнодействующая
внешнего давления приложена в точке
центра тяжести поверхности стенки.
Давление веса жидкости на стенку не
одинаково по высоте: чем глубже расположен
элемент стенки, тем большее давление
веса жидкости он испытывает. Поэтому
центр давления жидкости на вертикальную
стенку расположен всегда ниже центра
тяжести смоченной поверхности стенки.
Если вы помещаете твердый предмет на пол, давление на пол над областью контакта – это вес предмета, разделенного областью на полу. Хороший пример того, как сила на небольшой площади может привести к очень сильному давлению, наблюдается в обуви женщин с высокими шипами. Эти типы обуви могут нанести ущерб некоторым полам из-за очень высокого давления на пол на каблук.
Средний ботинок распределяет вес человека более 20 квадратных дюймов. В некоторых случаях этого достаточно, чтобы повредить пол. Если вы положите жидкость в контейнер, вес этой жидкости будет нажимать на дно контейнера, аналогичную весу твердого объекта. Давление на дно контейнера будет таким же, как если бы вес был из твердого вещества.
Сила полного гидростатического давления
на плоскую стенку равна произведению
гидростатического давления в центре
тяжести этой стенки и ее площади:
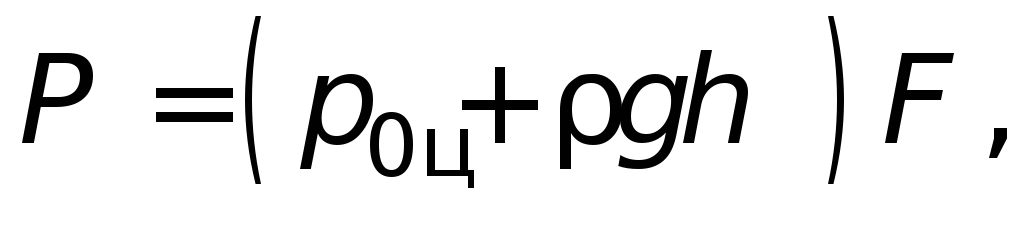 (1.10)
(1.10)
где
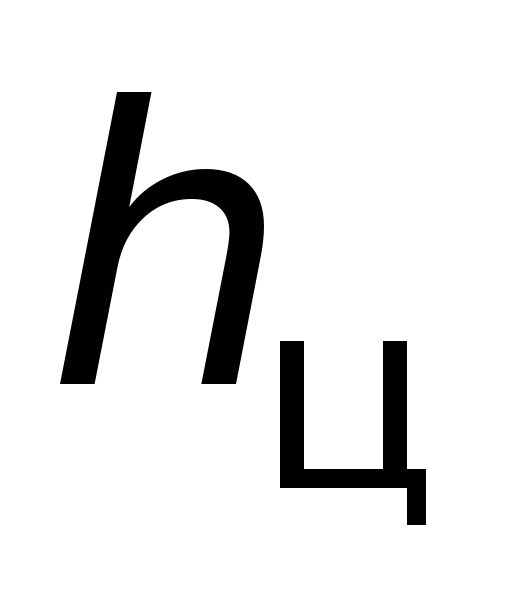 – расстояние от верхнего уровня жидкости
– расстояние от верхнего уровня жидкости
до центра тяжести смоченной поверхности
стенки; оно зависит от геометрической
формы стенки.
Единственное различие заключается в том, что давление в жидкости идет во все стороны. Таким образом, давление на сторонах внизу будет одинаковым. Газы и жидкости проявляют давление из-за их веса в каждой точке жидкости. Давление может быть измерено для твердого тела, нажимая на твердое тело, но в случае твердого тела, нажимающего на жидкость или газ, требуется, чтобы жидкость была ограничена в контейнере. Надавите на себя, чтобы преуспеть.
Самые популярные книги по физике силы. Если да, отправьте электронное письмо с отзывами. Пожалуйста, включите его в качестве ссылки на свой сайт или в качестве ссылки в своем отчете, документе или тезисе. Участники, подверженные воздействию осесимметричных нагрузок.
Точка приложения сил Р
иР
изб носит название центра давленияh
д и может быть определена в соответствии
с законами теоретической механики через
момент инерции смоченной поверхности
стенки
Тонкостенный цилиндр под давлением. Преамбула: сосуды высокого давления чрезвычайно важны в промышленности. Обычно в обычной практике используются два типа сосудов высокого давления, такие как цилиндрический сосуд высокого давления и сферический сосуд высокого давления.
При анализе этих стеновых цилиндров, подвергнутых внутренним давлениям, предполагается, что радиальные планы остаются радиальными, а доза толщины стенки не изменяется из-за внутреннего давления. Далее, при анализе их стеновых цилиндров, вес жидкости считается пренебрежимым.
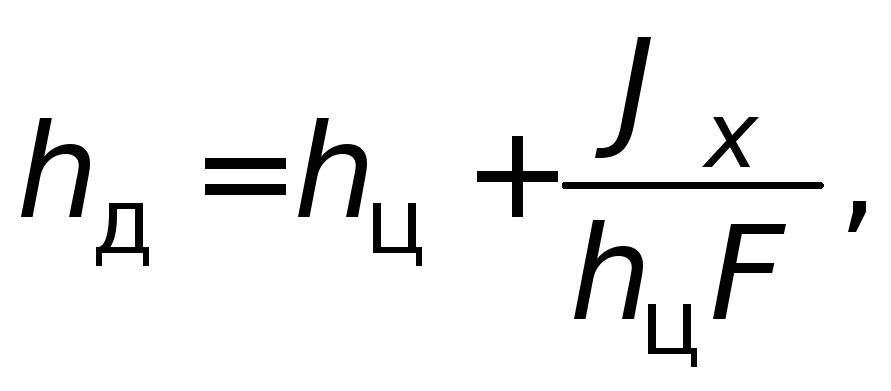 (1.11)
(1.11)
где J
x
– момент инерции
стенки относительно осиox
.
Для прямоугольной стенки при уровне
жидкости в сосуде, равном Н
, и ширине
стенкиВ
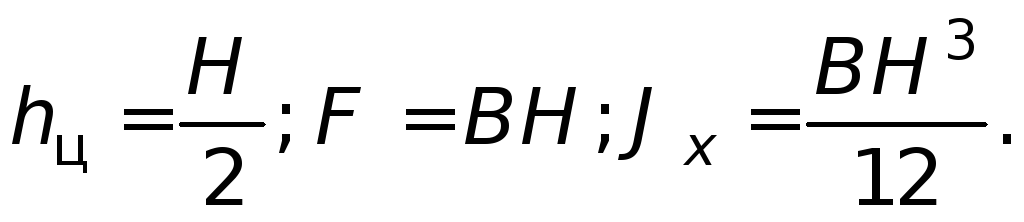
Следовательно,
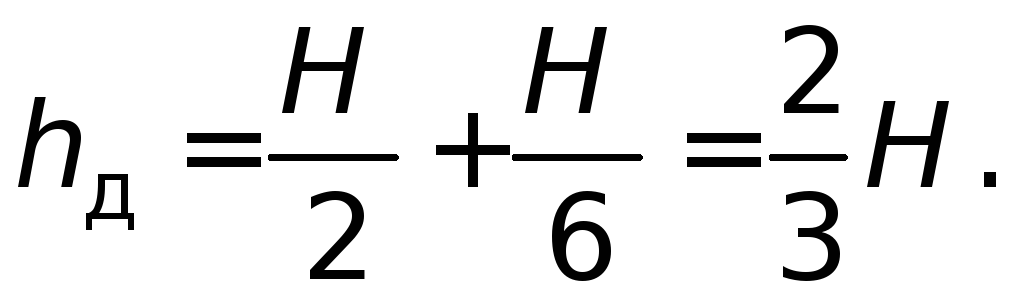
Этот цилиндр подвергается разности гидростатического давления р между его внутренней и внешней поверхностями. Во многих случаях р между давлением избыточного давления внутри цилиндра, заставляя внешнее давление быть окружающим. Небольшой кусок стенки цилиндра показан изолированно, а напряжения в соответствующем направлении также показаны.
Такой компонент не срабатывает, поскольку при чрезмерно высоком внутреннем давлении. Хотя это может потерпеть неудачу, разрываясь по пути, следующему окружности цилиндра. При нормальных обстоятельствах он терпит неудачу по обстоятельствам, которые он терпит неудачу, разрываясь вдоль пути, параллельного оси. Это говорит о том, что напряжение пялец значительно выше, чем осевое напряжение.
Практическое использование законов гидростатики
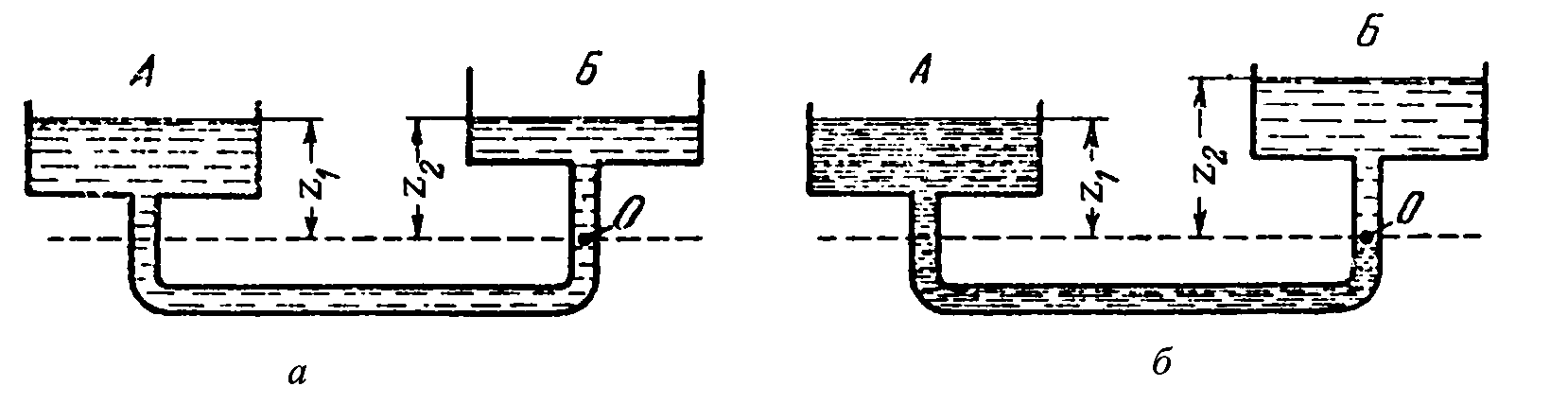
Применив закон Паскаля к сообщающимся
сосудам, можно прийти к следующим
выводам.
Если сосуды (рис. 1.4 а
) заполнены
однородной жидкостью (одинаковой
плотности), то при равновесии давление
в точке 0 может быть выражено:
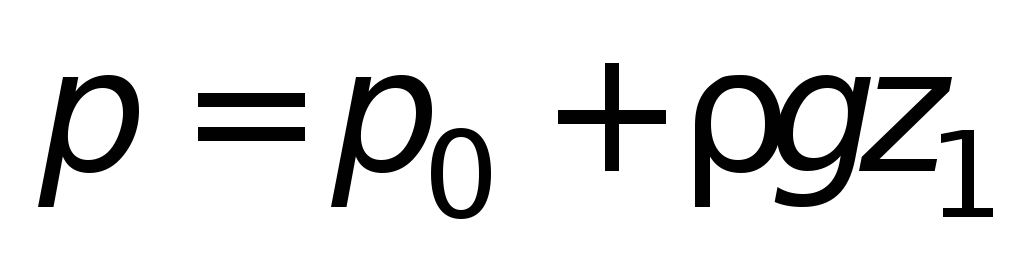 либо
либо
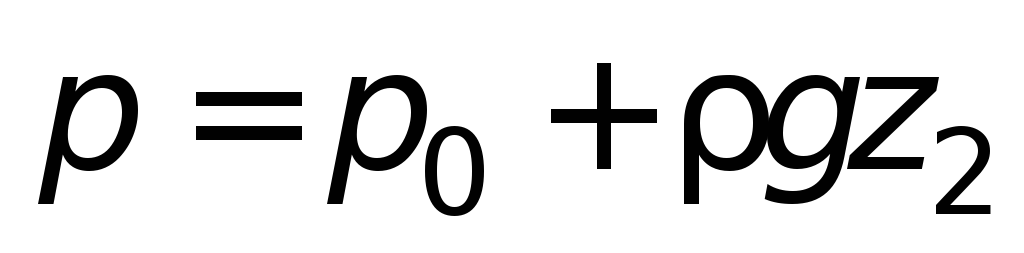 ,
,
Чтобы получить выражения для различных напряжений, сделаем следующее. Жидкие резервуары и емкости для хранения, водопроводные трубы, котлы, корпуса подводных лодок и некоторые компоненты воздушной плоскости являются общими примерами тонкостенных цилиндров и сфер, куполов крыши.
В стенке нет напряжений сдвига. Продольные и пястные напряжения не меняются через стену. Состояние выноса для элемента тонкостенного сосуда высокого давления считается двухосным, хотя внутреннее давление, действующее нормали к стене, вызывает локальное напряжение сжатия, равное внутреннему давлению. На самом деле состояние трехосевого напряжения существует на внутри судна. Однако для тогдашнего стенного сосуда давления третье напряжение намного меньше, чем два других напряжения, и по этой причине в этом можно пренебречь.
т.е. в сообщающихся сосудах заполняющая
их однородная жидкость располагается
на одинаковом уровне.
При заполнении сосудов жидкостями с
различной плотностью (рис 1.4 б
) в
условиях равновесия давление в точке
О будет
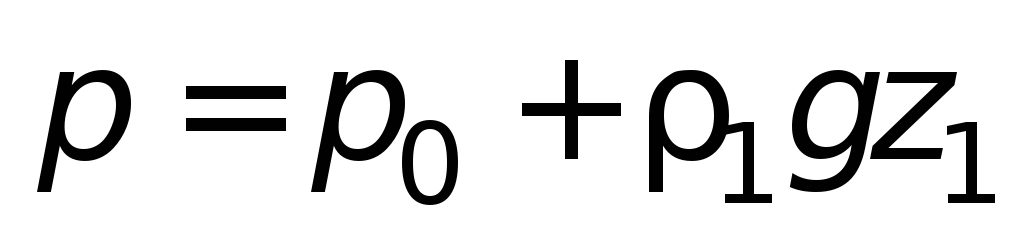 либо
либо
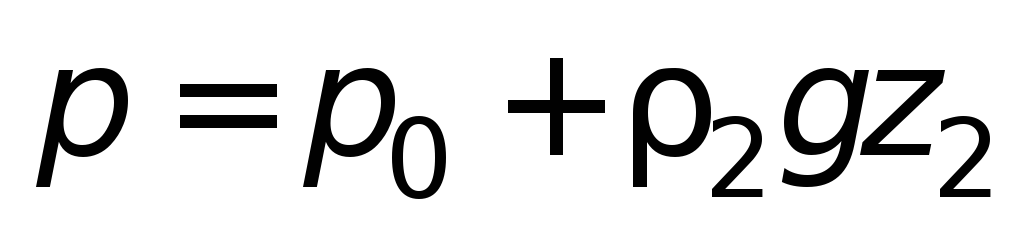 .
.
Тонкие цилиндры, подверженные внутреннему давлению. Когда тонкостенный цилиндр подвергается внутреннему давлению, в материалах цилиндра будут установлены три взаимно перпендикулярных главных напряжения, а именно. Окружность или шероховатость. Теперь определим эти напряжения и определим выражения для них.
Обруч или периферический стресс. Это напряжение, которое создается в противодействии разрушающему эффекту приложенного давления и может быть наиболее удобно обрабатываться с учетом равновесия цилиндра. На рисунке мы показали одну половину цилиндра. Общее усилие на одной половине цилиндра из-за внутреннего давления р.

Рисунок 1.4
– Сообщающиеся сосуды, заполненные
жидкостью:
а
– одной плотности;б
– разной плотности
Следовательно
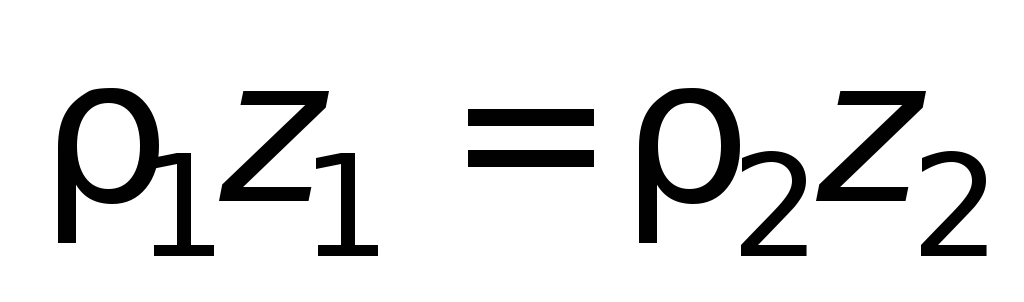 ,
,
т.е.
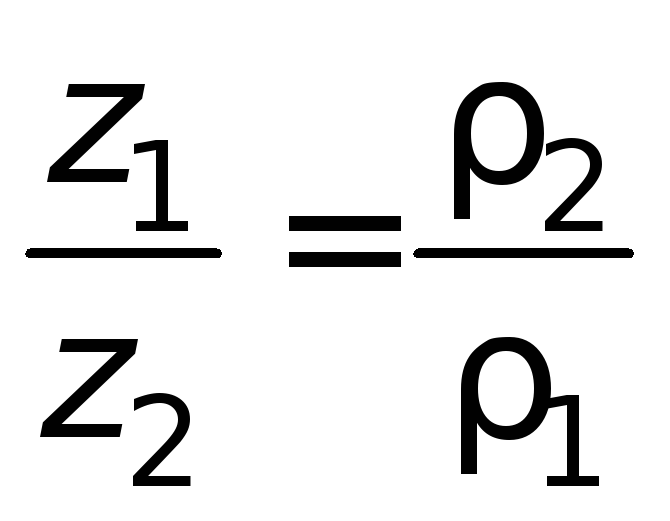 . (1.12)
. (1.12)
Т. – сила в одной стенке полуцилиндра. Требования к сложным системам автоматизированной обработки, потребность во все более жестком управлении технологическими процессами и все более строгая нормативная среда приводят к тому, что инженеры-разработчики стремятся получать более точные и надежные системы измерения уровня. Повышенная точность позволяет снизить изменчивость химического процесса, что приводит к повышению качества продукта, снижению затрат и меньшему количеству отходов. Правила, особенно касающиеся электронных документов, устанавливают жесткие требования к точности, надежности и электронной отчетности.
Соотношение (1.12) указывает на то, что
высоты уровней жидкости, отсчитываемые
от поверхности раздела, обратно
пропорциональны плотностям жидкостей.
Этот принцип используется для измерения
уровня жидкости в закрытых аппаратах
с помощью водомерных стёкол, в жидкостных
манометрах.
Если сообщающиеся сосуды заполнены
одной и той же жидкостью, но давление
над уровнем жидкости в них разное – р
1 ир
2 , то при равновесии
Технология измерения уровня в переходном периоде
Новые технологии измерения уровня помогают удовлетворить эти требования. Простейшим и самым старым промышленным устройством, конечно же, является смотровое стекло. Ручной подход к измерению, очки зрения всегда имели ряд ограничений. Уплотнения подвержены утечке, а наращивание, если оно присутствует, скрывает видимый уровень. Можно безоговорочно заявить, что обычные смотровые стекла являются самым слабым звеном любой установки. Поэтому их быстро заменяют более современные технологии.
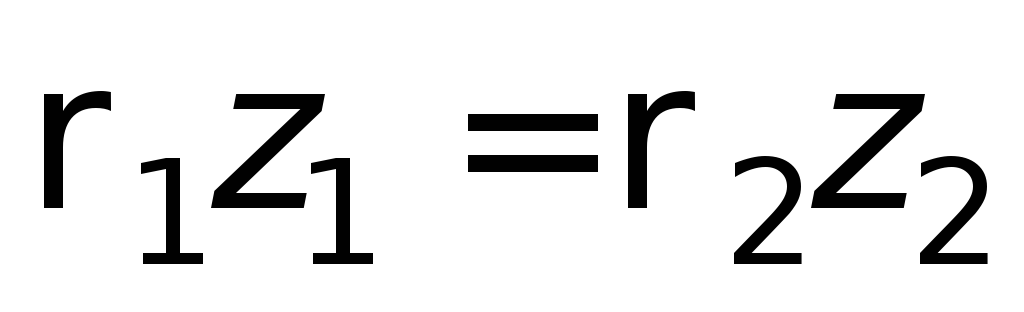 ,
,
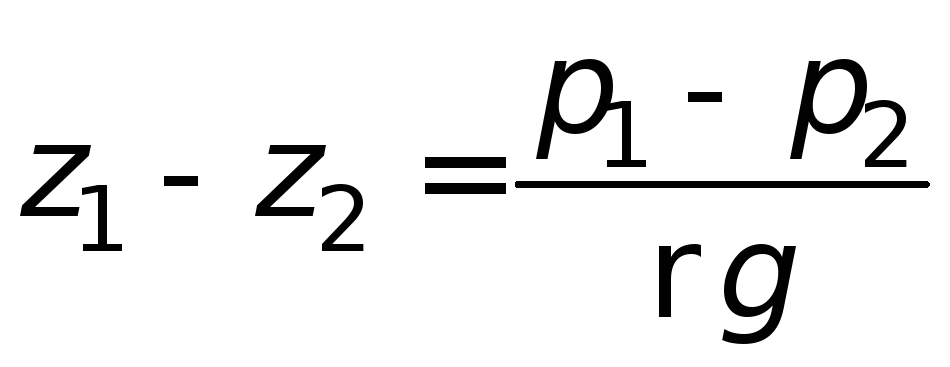 . (1.13)
. (1.13)
Последнее выражение используется при
измерении давления или разности давлений
между различными точками с помощью
дифференциальных U
-образных
манометров.
Другие устройства обнаружения уровня включают те, которые основаны на удельном весе, физическом свойстве, наиболее часто используемом для восприятия поверхности уровня. Простой поплавок, имеющий удельный вес между потоками технологической жидкости и паром свободного пространства, будет плавать на поверхности, точно после ее подъемов и падений. Измерения гидростатической головки также широко использовались для определения уровня.
Когда задействованы более сложные физические принципы, возникающие технологии часто используют компьютеры для выполнения вычислений. Это требует отправки данных в машиночитаемом формате от датчика к системе управления или мониторинга. Полезными форматами выходных сигналов преобразователя для компьютерной автоматизации являются токовые петли, аналоговые напряжения и цифровые сигналы. Аналоговые напряжения просты в настройке и работе, но могут иметь серьезные проблемы с помехами и помехами.
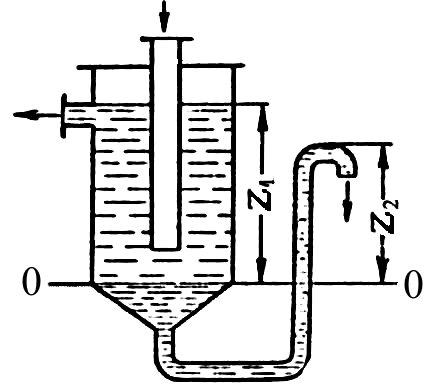
Рисунок 1.5.
– К определению высоты гидравлического
затвора
Этот же принцип используется для
определения высоты гидравлического
затвора в аппаратах, заполненных
жидкостью (рис. 1.5).
На рисунке представлен сосуд, заполненный
двумя жидкостями с плотностями 1 и 2 ; уровень
их раздела на глубинеz
1 необходимо поддерживать в процессе
работы постоянным с помощью гидрозатвора,
представляющего собойU
-образную
трубку, подсоединённую снизу (на выходе
жидкости из аппарата).
В соответствии с уравнением (1.12) высота
гидравлического затвора в случае
одинакового давления над жидкостью
внутри аппарата и на выходе из затвора
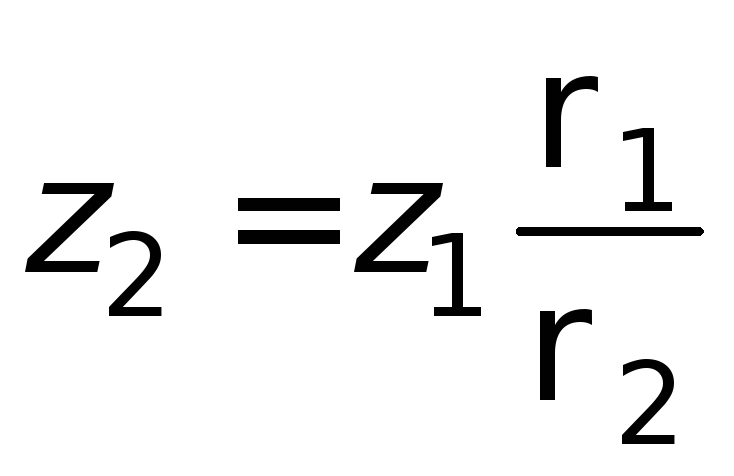 . (1.14)
. (1.14)
На использовании данного уравнения
гидростатики основана работа таких
простейших гидравлических машин, как
гидравлический пресс, мультипликатор
(для повышения давления), домкрат,
подъемник и др.
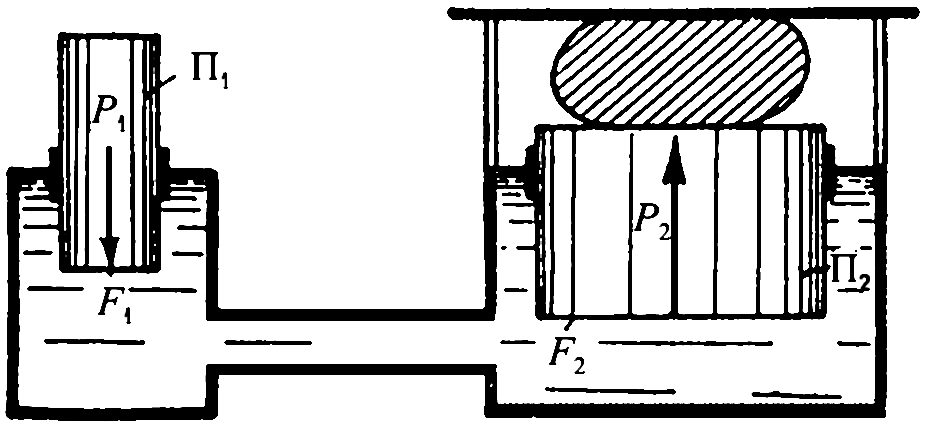
Рисунок 1.6
– Схема гидравлического пресса
На рис. 1.6 показана схема
гидравлического пресса. Если к поршню
П 1 , имеюшему площадьF
1 ,
приложена силаР
1 , то эта сила
будет передаваться на жидкость; жидкость
же будет давить на поршень П 2 ,
имеющий площадьF
2 , с силойР
2
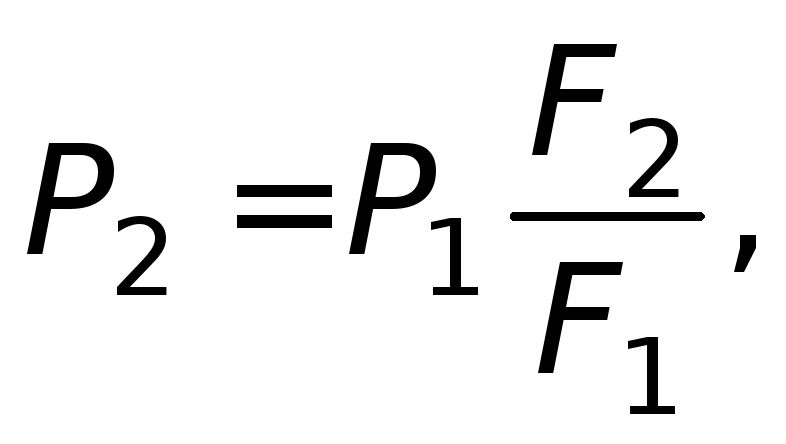 (1.15)
(1.15)
так как гидростатические давления в
точках площади F
1 и площадиF
2 практически равны между собой:
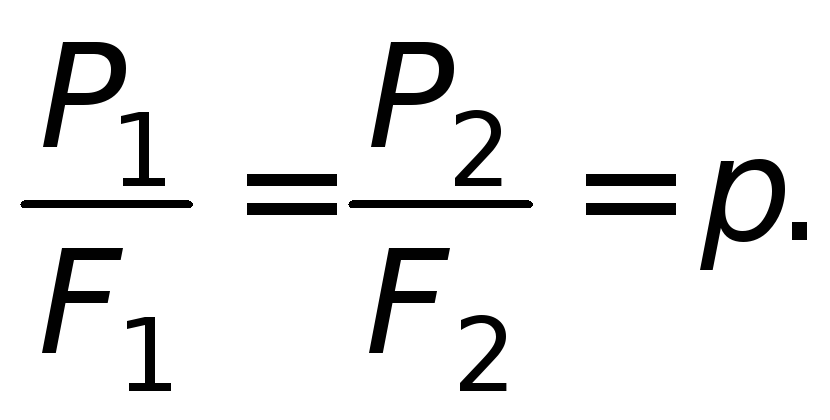 (1.16)
(1.16)
Из уравнения (1.16) следует, что при помощи
пресса сила Р
1 увеличивается
во столько раз, во сколько площадьF
2 больше площадиF
1 .
Источник
§ 40. Расчёт давления жидкости на дно и стенки сосуда
Рассмотрим, как можно рассчитать давление жидкости на дно и стенки сосуда. Решим сначала задачу для сосуда, имеющего форму прямоугольного параллелепипеда (рис. 112).
Сила F, с которой жидкость, налитая в этот сосуд, давит на его дно, равна весу Р жидкости, находящейся в сосуде. Вес жидкости можно определить, зная её массу m. Массу, как известно, можно вычислить по формуле m = ρV. Объём жидкости, налитой в выбранный нами сосуд, легко рассчитать. Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V=Sh.
Масса жидкости m = ρV, или m = ρSh.
Вес этой жидкости Р = gm, или Р = gρSh.
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес Р на площадь S, получим давление жидкости р:
Мы получили формулу для расчёта давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
Следовательно, по выведенной формуле можно рассчитывать давление жидкости, налитой в сосуд любой формы. Кроме того, по ней можно вычислить и давление на стенки сосуда. Давление внутри жидкости, в том числе давление снизу вверх, также рассчитывается по этой формуле, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчёте давления по формуле р = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м 3 ), а высоту столба жидкости h — в метрах (м), g = 9,8 H/кг, тогда давление будет выражено в паскалях (Па).
П р и м е р. Определите давление нефти на дно цистерны, если высота столба нефти 10 м, плотность 800 кг/м 3 .
Запишем условие задачи и решим её.
Вопросы
1. Выведите формулу для расчёта давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда.
2. От каких величин и как зависит давление жидкости на дно сосуда?
3. По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?
Упражнение 17
1. Определите давление на глубине 0,6 м в воде, керосине, ртути.
2. Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой 10 900 м. Плотность морской воды 1030 кг/м 3 .
3. На рисунке 113 изображена футбольная камера, соединённая с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на неё — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.
Задание
1. Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рис. 114). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?
2. Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.
Источник
Расчет давления жидкости на дно и стенки сосуда
Разделы: Физика
«Кто смолоду больше делает и думает сам, тот становится потом надежнее, крепче, умнее». С. Нерис
Цели урока:
- Образовательные:
- активизировать знания учащихся о причинах возникновения давления жидкости,
- создать условия для овладения учащимися формулы для расчета давления жидкости на дно и стенки сосуда,
- продолжить работу по формированию навыков научного познания мира,
- создать условия для овладения учащимися эвристическим методом представления наблюдаемого явления – методом графических образов.
- Развивающие:
- развивать экспериментальные умения, навыки логического мышления, умение обосновывать свои высказывания, делать выводы, выделять главное, представлять информацию в различных знаковых системах,
- развивать у учащихся интерес к познанию законов природы и их применению;
- развивать умение проводить рефлексию своей деятельности.
- Воспитательные:
- создать условия для приобретения убежденности учащихся в познаваемости окружающего мира,
- приучать учащихся к доброжелательному общению, взаимопомощи, к самооценке.
Задачи урока:
- изучение теоретического материала;
- решение задач на расчет давления в жидкости и газе;
- практическое значение знаний о давлении жидкости.
План урока:
- Организационный момент. (1 мин.)
- Актуализация знаний. (5 мин.)
- Объяснение материала. (20 мин.)
- Закрепление материала. (15 мин.)
- Рефлексия. (2 мин.)
- Домашнее задание. (2 мин.)
Ход урока
I. Организационный момент.
(На партах учащихся лежат рабочие карты урока, в которых представлены две самостоятельные работы и критерии выставления оценки; две ручки с разными стержнями, например синий и зеленый; таблицы плотностей веществ, учебники и тетради).
II. Актуализация знаний.
III. Объяснение нового материала
Провожу эксперимент: в пластмассовую бутылку с тремя отверстиями на разных уровнях по высоте наливаем подкрашенную воду.
- почему вода вытекает из сосуда?
- сравните струи воды?
- объясните, почему они разные?
Когда учащиеся объяснят, что столбы жидкости разные и давление на разной глубине разное, ставлю проблему: а нужно ли знать людям, чему равно давление жидкости на разных глубинах, на дно, на стенки сосуда?
Открываем тетради, записываем тему урока.
Ставим цель: вывести формулу для расчета давления жидкости на дно и стенки сосуда.
Давление жидкости (см. презентация)
Вокруг нас много жидкостей. Одни из них движутся, например, вода в реках или нефть в трубах, другие – покоятся. При этом все они имеют вес и поэтому давят на дно и стенки сосуда, в котором находятся. Подсчет давления движущейся жидкости – непростая задача, поэтому изучим лишь как рассчитывать давление, создаваемое весом покоящейся жидкости. Оно называется гидростатическим давлением и вычисляется по следующей формуле.
| p – давление слоя жидкости, Па |
| ρ – плотность жидкости, кг/м3 |
| g – коэффициент, Н/кг |
| h – высота слоя жидкости, м |
Рассмотрим, как выведена эта формула. Сила F, с которой жидкость давит на дно сосуда, является весом жидкости. Его мы можем подсчитать по формуле F тяж = mg, так как жидкость и ее опора (дно сосуда) покоятся. Вспомним также формулу m = ρV для выражения массы тела через плотность его вещества и формулу V = Sh для подсчета объема тела, имеющего форму прямоугольного параллелепипеда. В результате имеем равенство:
Это равенство иллюстрирует не только способ вывода формулы для вычисления гидростатического давления. Оно также показывает, что формула p = ρgh является частным случаем определения давления – формулы p = F/S.
Заметим также, что при выводе формулы совсем необязательно предполагать, что слой высотой h и плотностью ρ образован именно жидкостью. В наших рассуждениях ничего не изменится, если вместо давления жидкости мы рассмотрим давление твердого тела прямоугольной формы или даже газа, заключенного в соответствующий сосуд. Создаваемое ими весовое давление будет именно таким, как предсказывает формула p = ρgh.
Формула p = ρgh показывает, что давление, создаваемое слоем жидкости, не зависит от ее массы, а зависит от плотности жидкости, высоты ее слоя и места наблюдения. При увеличении толщины слоя жидкости или ее плотности гидростатическое давление будет возрастать.
Полученный нами вывод можно проверить опытами. Проделаем их. Справа изображена стеклянная трубка с водой, дно которой затянуто тонкой резиновой пленкой. Увеличивая высоту слоя налитой жидкости, мы будем наблюдать увеличение растяжения пленки. Этот опыт подтверждает, что при увеличении высоты слоя жидкости создаваемое ею давление увеличивается.
На следующем рисунке изображены трубки с водой и «крепким» раствором соли. Видно, что уровни жидкостей находятся на одной и той же высоте, но давление на пленку в правой трубке больше. Это объясняется тем, что плотность раствора соли больше, чем плотность обычной воды.
На доске нарисован параллелепипед высотой h и площадью основания S. Предлагаю ребятам представить, что это аквариум, в котором налита вода. Попытаемся определять давление воды Р на дно аквариума. Работаем на магнитной доске с карточками, выкладывая поочередно формулы, получая цепочку: m=ρV, V=Sh, m=ρSh, P=gm, P=gρSh, ρ=P/S, p=ρgh.
Анализируем окончательную формулу: что же нужно знать, чтобы рассчитать давление жидкости.
Зависит ли давление от площади или формы сосуда?
Вьполняем фронтальный эксперимент: на каждой парте стоит стакан с водой. Высота налитой воды одинаковая.
Цель: определить давление воды на дно стакана.
Один ученик выполняет у доски. Остальные за партой. Сверяем ответ. Анализируем его: какую физическую величину мы измеряли? какую физическую величину брали в таблице? какое численное значение давления получили учащиеся, работающие за партой и у доски? большое это или маленькое давление?
IV. Закрепление изученного материала.
Приведи примеры движущихся жидкостей.
Произведение в правой части формулы для вычисления гидростатического давления представляет собой .
По какой формуле мы сможем подсчитать вес покоящейся жидкости?
О чем говорит равенство p=ρgh?
Как можно подтвердить справедливость формулы p=ρgh?
Увеличение растяжения пленки свидетельствует, что .
Описанный опыт иллюстрирует зависимость гидростатического давления от ..
Плотность раствора соли больше, чем плотность воды. Это приводит к тому, что .
а) Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, если бы она была налита вместо воды?
б) Какое давление на дно сосуда оказывает слой керосина высотой 1,5 м?
в) Волк плывет под водой с дыхательной трубкой. Какие ограничения накладывает на ныряльщика дыхательная трубка? Ответ найдите в учебнике стр. 95.
Задача с недостающими данными
г) Какое давление на глубине 1,5 м? Решить устно.
Качественные задачи, предполагающие работу с дополнительными источниками информации
д) Какое преимущество дает ныряльщику акваланг? Какие ограничения он накладывает? Ответ в учебнике.
е) В следующем сюжете мы видим глубоководный аппарат. Почему у него такая внешняя форма?
ж) Чтобы человек мог работать на больших глубинах он должен находиться в специальном скафандре. Найдите о нем информацию в учебнике.
з) Анализируя рис. 103 учебника давайте познакомимся с тем, что говорит нам учебник о глубоководных аппаратах. Какие ограничения в их использовании имеются?
и) Вычислите, какое давление в самой глубокой Мариинской впадине глубиной.
к) В просмотренном сюжете мы видели с вами глубоководных рыб. Какую длину лески нужно приготовить для лова рыбы камбалы, если она может выдерживать давление 400 кПа.
V. Задаю домашнее задание:
параграф из учебника, упражнение на решение задач и сообщения:
- «Человек изучает подводный мир».
- «Подводные лодки, батисферы и батискафы».
- «Животный мир океанских и морских глубин».
- «Ныряльщики за жемчугом».
Источник
По какой формуле рассчитывается давление на дно стенки сосуда
В ходе этого урока с помощью математических преобразований и логических умозаключений будет получена формула для расчета давления жидкости на дно и стенки сосуда.
Тема: Давление твердых тел, жидкостей и газов
Урок: Расчет давления жидкости на дно и стенки сосуда
Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 1).
Рис. 1. Сосуд для расчета давления жидкости
Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу, действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде
Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m
Напомним, что символом g обозначено ускорение свободного падения.
Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V
Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда
Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:
В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:
Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.
Полученная выше формула называется формулой гидростатического давления. Она позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.
Рассмотрим несколько примеров.
Возьмем два сосуда. В одном из них находится вода, а в другом – подсолнечное масло. Уровень жидкости в обоих сосудах одинаков. Одинаковым ли будет давление этих жидкостей на дно сосудов? Безусловно, нет. В формулу для расчета гидростатического давления входит плотность жидкости. Поскольку плотность подсолнечного масла меньше, чем плотность воды, а высота столба жидкостей одинакова, то масло будет оказывать на дно меньшее давление, чем вода (Рис. 2).
Рис. 2. Жидкости с различной плотностью при одной высоте столба оказывают на дно различные давления
Еще один пример. Имеются три различных по форме сосуда. В них до одного уровня налита одна и та же жидкость. Будет ли одинаковым давление на дно сосудов? Ведь масса, а значит, и вес жидкостей в сосудах различен. Да, давление будет одинаковым (Рис. 3). Ведь в формуле гидростатического давления нет никакого упоминания о форме сосуда, площади его дна и весе налитой в него жидкости. Давление определяется исключительно плотностью жидкости и высотой ее столба.
Рис. 3. Давление жидкости не зависит от формы сосуда
Мы получили формулу для нахождения давления жидкости на дно и стенки сосуда. Этой формулой можно пользоваться и для расчета давления в объеме жидкости на заданной глубине. Она может быть использована для определения глубины погружения аквалангиста, при расчете конструкции батискафов, подводных лодок, для решения множества других научных и инженерных задач.
Список литературы
- Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
- Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Единая коллекция цифровых образовательных ресурсов (Источник).
- Единая коллекция цифровых образовательных ресурсов (Источник).
Домашнее задание
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов №504–513.
Источник
Источник
