Как решать задачи с сосудами егэ

В
заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о
погружении детали в жидкость или о переливании жидкости из одного сосуда
в другой.
Вопросы
в условии связаны с нахождением объёма погружаемого в жидкость тела или
с нахождением какого-либо параметра сосуда. Форма сосуда может быть
различной: цилиндр, призма.
Что необходимо понимать?
Если
жидкость залита в цилиндрический сосуд, то она принимает форму
цилиндра. Если она залита в имеющий форму призмы, то соответственно
принимает форму призмы. Это означает, что формулы для объёмов цилиндра и
призмы работают и для объёмов жидкостей помещённых в такие сосуды.
Формула объёма (цилиндра и призмы):
Если
жидкость перливается в аналогичный сосуд с меньшим основанием, уровень
(высота) жидкости увеличивается; если в сосуд с большим основанием, то
уровень жидкости уменьшается.
Рекомендации!
В
задачах на погружение детали в жидкость следует найти объём полученный
после её погружения, далее найти разность объёмов до и после (если
данные в условии это позволяют). Можно такие задачи решать и другим
способом, используя закон Архимеда. Примеры рассмотрены ниже.
В
задачах, где идёт речь о переливании жидкости в другой сосуд (с
уменьшенной или увеличенной площадью основания) помните о том, что сам
объём жидкости остаётся неизменным. Вы можете выразить его через площадь
основания и высоту (S1 и H1) одного сосуда и площадь основания и высоту (S2 и H2) другого сосуда, далее полученные выражения приравнять.
При
дальнейших преобразованиях получите отношение соответствующих величин –
либо площадей оснований, их рёбер, либо высот. Пример такой задачи
рассмотрен ниже в статье.
В цилиндрический сосуд налили 5000 см3
воды. Уровень жидкости оказался равным 40 см. В воду полностью
погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см.
Чему равен объем детали? Ответ выразите в см3.
Мы знаем, что объём цилиндра равна произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Высота это есть уровень жидкости.
Итак, из имеющихся данных можем найти площадь основания:
Основание
цилиндра у нас величина неизменная, но изменилась высота жидкости (при
погружении детали) на 15 сантиметров, то есть она стала
40 +15 = 55 см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 6875 – 5000 = 1875 см3
Можно решать подобные задачи более рациональным способом.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/45 исходного объема:
Ответ: 1875
Решить самостоятельно:
Посмотреть решение
В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см3 воды
и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде
поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали?
Ответ выразите в см3.
Принцип решения тот же самый, что и в предыдущей задаче.
Мы знаем, что объём призмы равен произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Из имеющихся данных можем найти площадь основания призмы:
Основание призмы не изменилось, но изменилась высота жидкости (при погружении детали) она стала 24см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 3000 – 2500 = 500 см3
Второй способ:
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20 исходного объема:
Ответ: 500
Решить самостоятельно:
Посмотреть решение
В
сосуд, имеющий форму правильной треугольной призмы, налили воду.
Уровень воды достигает 250 см. На какой высоте будет находиться уровень
воды, если ее перелить в другой такой же сосуд, у которого сторона
основания в 5 раз больше, чем у первого? Ответ выразите в см.
В
подобных задачах с переливаниями жидкости следует помнить, что объём её
остаётся прежним (он не изменен – куда бы её не перелили).
Объем
жидкости в данном случае это объём правильной треугольной призмы (в
её основании лежит правильный треугольник). Он равен произведению
площади основания призмы на высоту:
Суть
дальнейших действий сводится к тому, что мы можем выразить объёмы
жидкостей в двух призмах: первой и второй (основание которой в 4 раза
больше), а затем приравнять полученные выражения, в итоге после
преобразований получим отношение двух высот.
Естественно, что высота жидкости уменьшится, если увеличить площадь основания.
Обозначим исходную высоту жидкости Н1, полученную после переливания Н2.
Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:
Таким образом, объём залитой жидкости в первую призму равен:
Площадь основания второй призмы равна:
Объём залитой жидкости во вторую призму равен:
Найдём отношение высот:
Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.
Или можно сказать так:
При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.
Ответ: 10
Решить самостоятельно:
Посмотреть решение
В
цилиндрический сосуд, в котором находится 14 литров воды, опущена
деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему
равен объем детали? Ответ выразите в литрах.
Объём цилиндра равна произведению площади его основания на высоту:
Жидкость в сосуде имеет цилиндрическую объёмную форму.
Уровень
жидкости поднялся в 1,1 раза – означает, что высота цилиндра
увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что
при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также
в 1,1 раза (так как зависимость величин прямопропорциональная).
Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.
Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.
Ответ: 1,4
Решить самостоятельно:
Посмотреть решение
Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?
Например,
если дан начальный объём и высота жидкости (в сосуде формы призмы или
цилиндра), то мы можем найти площадь основания. Затем, зная площадь
основания и высоту жидкости после погружения детали мы можем найти
полученный объём.
Далее
найти разницу между объёмами не составит труда (это относится к первым
двум задачам). В последней задаче для решения требуется немного
логики.
Источник
Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
. В сосуд, содержащий литров -процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
.
. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:
Ответ: .
. Виноград содержит влаги, а изюм — . Сколько килограммов винограда требуется для получения килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было . В изюме воды и «сухого вещества». Пусть из кг винограда получилось кг изюма. Тогда
от от
Составим уравнение:
и найдем .
Ответ: .
. Имеется два сплава. Первый сплав содержит никеля, второй — никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

Запишем простую систему уравнений:
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что .
Ответ: .
. Смешав -процентный и -процентный растворы кислоты и добавив кг чистой воды, получили -процентный раствор кислоты. Если бы вместо кг воды добавили кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?
Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна . Запишем два уравнения, для количества кислоты.
Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
Ответ: .
Источник
МБОУ Пожарская СОШ Сергачского района Нижегородской области
Учитель математики первой категории Зюляева Л.Ю.
Задания для подготовки к ЕГЭ
11 класс по теме «Цилиндр»
Задачи по готовым чертежам
1 вариант
1. Осевое сечение цилиндра – квадрат со стороной 6 см. Найти сумму высоты и радиуса основания цилиндра.
2. Радиус основания цилиндра равен 2м, высота 3м. Найти диагональ осевого сечения.
3. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
Задачи по готовым чертежам
2 вариант
1. Осевое сечение цилиндра – квадрат со стороной 8 см. Найти сумму высоты и радиуса основания цилиндра.
2. Радиус основания цилиндра равен 4м, высота 6м. Найти диагональ осевого сечения.
3. Длина окружности основания цилиндра равна 2. Площадь боковой поверхности равна 1. Найдите высоту цилиндра.
Типы задач на ЕГЭ по теме «Площадь боковой поверхности цилиндра»
1 Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 300. Найдите радиус цилиндра.
2. Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 450 и равна 8√2 см. Найдите площадь боковой поверхности цилиндра, деленную на π .
4.Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?
Типы задач | № задачи | |
1 тип задач | Задачи, решаемые в одно действие с помощью т. Пифагора или свойства прямоугольного треугольника | |
2 тип задач | Задачи, решаемые в одно действие с помощью формулы площади боковой поверхности. | |
3 тип задач | Задачи, решаемые в два действия с помощью т. Пифагора и формулы площади боковой поверхности. |
Задания по теме «Площадь поверхности цилиндра»
ЕГЭ 2015 Задания из Открытого банка заданий. Математика. Геометрия.
Прототипы заданий №12
Задание №27133
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Задание №245358
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Задание №27058
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
Проверочная тестовая работа Вариант 1
№1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности, деленная на π, равна:
40; 10; 20; 4
№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π.
80; 96; 64; 32
№3. Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности, деленная на π, равна:
16; 32; 4; 8
№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, деленная на π, равна:
56; 72; 88; 48
№5. Если площадь боковой поверхности цилиндра равна 64π кв.м, а высота – 4 м, тогда радиус равен:
16; 8; 26; 8π
№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:
256; 100; 24; 64
№7. Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра, деленная на π, может быть равна:
36; 64; 48; 96
Проверочная тестовая работа
Вариант 2.
№1. Диаметр основания цилиндра равен 4 см, высота – 3 см, тогда площадь боковой поверхности, деленная на π, равна:
40; 10; 12; 4
№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 9π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π .
40; 54; 60; 32
№3. Радиус основания цилиндра в три раза меньше образующей, равной 6, тогда площадь боковой поверхности, деленная на π, равна:
24; 32; 4; 8
№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его меньшей стороны, деленная на π, равна:
56; 105; 154; 48
№5. Если площадь боковой поверхности цилиндра равна 64π кв.м, а радиус – 8м, тогда образующая равна:
16; 4; 26; 8π
№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:
256; 100; 24; 25
№7. Осевым сечением цилиндра является прямоугольник со сторонами 6 и 8 см, то площадь боковой поверхности цилиндра может быть равна:
9; 64; 36; 48
Ключ к тестовой работе (оба варианта)
№ задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Ответ | 3 | 2 | 1 | 3 | 2 | 4 | 4 |
Источник
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
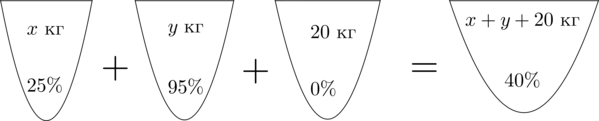
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
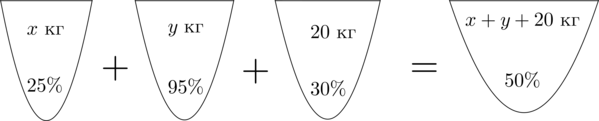
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20
Источник
