Как узнать давление газа в сосуде
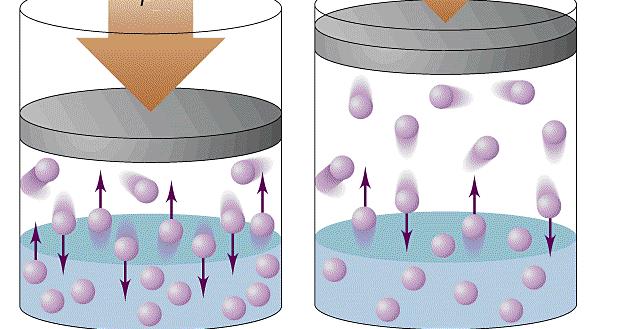
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
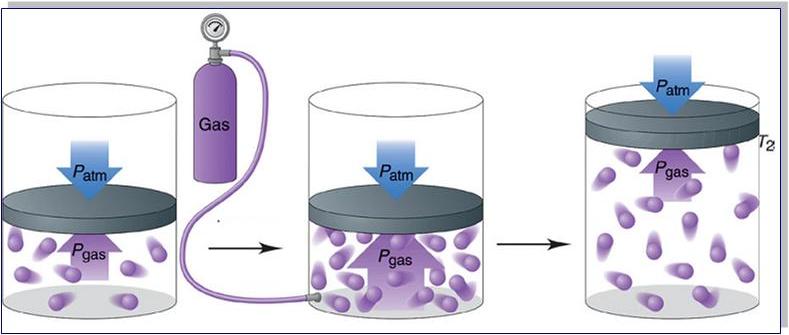
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории

При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
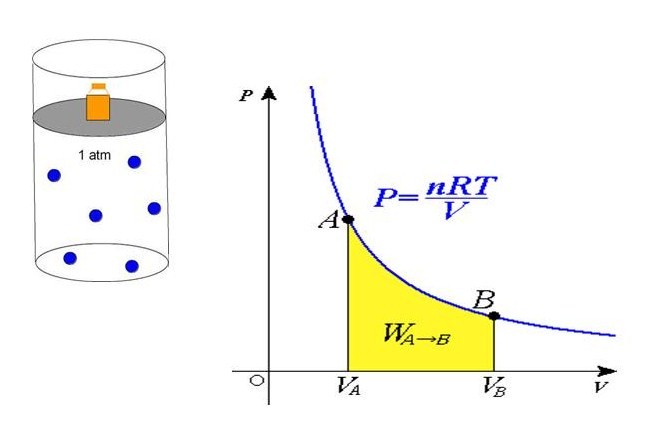
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
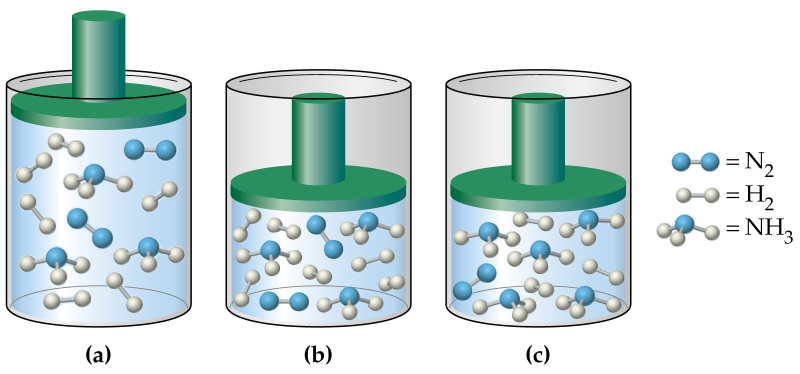
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.

Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.

Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.

Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.

Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
Источник
Школьная Энциклопедия
Nav view search
Навигация
Искать
Давление газа
Где бы ни находился газ: в воздушном шаре, автомобильной шине, или металлическом баллоне — он заполняет собой весь объём сосуда, в котором находится.
Давление газа возникает совсем по другой причине, нежели давление твёрдого тела. Оно образуется в результате ударов молекул о стенки сосуда.
Давление газа на стенки сосуда
Двигаясь хаотично в пространстве, молекулы газа сталкиваются между собой и со стенками сосуда, в котором находятся. Сила удара одной молекулы мала. Но так как молекул очень много, и сталкиваются они с большой частотой, то, действуя сообща на стенки сосуда, они создают значительное давление. Если в газ помещено твёрдое тело, то оно также подвергается ударам молекул газа.
Проведём несложный опыт. Под колокол воздушного насоса поместим завязанный воздушный шарик, не полностью наполненный воздухом. Так как воздуха в нём мало, шарик имеет неправильную форму. Когда же мы начнём откачивать воздух из-под колокола, шарик станет раздуваться. Через некоторое время он примет форму правильного шара.
Что же произошло с нашим шариком? Ведь он был завязан, следовательно, количество воздуха в нём осталось прежним.
Всё объясняется довольно просто. Во время движения молекулы газа сталкиваются с оболочкой шарика снаружи и внутри него. Если воздух откачивается из колокола, молекул становится меньше. Уменьшается плотность, а значит и частота ударов молекул о наружную оболочку также уменьшается. Следовательно, давление снаружи оболочки падает. А так как внутри оболочки число молекул осталось прежним, то внутреннее давление превышает наружное. Газ давит изнутри на оболочку. И по этой причине она постепенно раздувается и принимает форму шара.
Закон Паскаля для газов
Молекулы газа очень подвижны. Благодаря этому давление они передают не только в направлении действия силы, вызывающей это давление, но и равномерно по всем направлениям. Закон о передаче давления сформулировал французский учёный Блез Паскаль: «Давление, производимое на газ или жидкость, передаётся без изменений в любую точку по всем направлениям». Этот закон называют основным законом гидростатики — науки о жидкости и газе в состоянии равновесия.
Закон Паскаля подтверждается опытом с прибором, который называют шаром Паскаля. Этот прибор представляет собой шар из твёрдого вещества с проделанными в нём крошечными отверстиями, соединённый с цилиндром, по которому двигается поршень. Шар заполняется дымом. При сжатии поршнем дым выталкивается из отверстий шара одинаковыми струйками.
Давление газа вычисляют по формуле:
где еlin — средняя кинетическая энергия поступательного движения молекул газа;
n — концентрация молекул
Парциальное давление. Закон Дальтона
На практике чаще всего нам приходится встречаться не с чистыми газами, а с их смесями. Мы дышим воздухом, являющимся смесью газов. Выхлопные газы автомобилей — тоже смесь. При сварке уже давно не применяется чистый углекислый газ. Вместо него также используют газовые смеси.
Газовой смесью называют смесь газов, не вступающих в химические реакции между собой.
Давление отдельного компонента газовой смеси называется парциальным давлением.
Если предположить, что все газы смеси являются идеальными газами, то давление смеси определяется законом Дальтона: «Давление смеси идеальных газов, не взаимодействующих химически, равно сумме парциальных давлений».
Его величина определяется по формуле:
Каждый газ в смеси создаёт парциальное давление. Его температура равна температуре смеси.
Давление газа можно изменить, меняя его плотность. Чем больше газа будет закачано в металлический баллон, тем больше в нём будет молекул, ударяющихся о стенки, и тем выше станет его давление. Соответственно, откачивая газ, мы разрежаем его, и давление снижается.
Но давление газа также можно изменить, изменив его объём или температуру, то есть, сжав газ. Сжатие проводят, воздействуя силой на газообразное тело. В результате такого воздействия уменьшается занимаемый им объём, повышается давление и температура.
Газ сжимается в цилиндре двигателя при движении поршня. На производстве высокое давление газа создают, сжимая его с помощью сложных устройств — компрессоров, которые способны создать давление до нескольких тысяч атмосфер.
Источник
Как рассчитать давление в сосуде
- Сосуд
- Жидкость с известной плотностью
- Знание закона Паскаля
- Ареометр или пикнометр
- Мерная мензурка
- Весы
- Таблица поправок для взвешивания на воздухе
- Линейка
Лучше пользоваться набором ареометров, в который входят приборы для измерения плотности жидкостей легче или тяжелее воды. Существуют специальные ареометры для измерения плотности спирта, молока и некоторых других жидкостей.
Чтобы измерить плотность жидкости ареометром, сосуд должен быть не менее 0,5 л.
Если рассматривать жидкость как несжимаемую, то давление на все поверхности сосуда будет равномерным.
Измерение плотность с помощью пикнометра более точное, хотя и более трудоемкое. Вам понадобятся еще аналитические весы, дистиллированная вода, спирт, эфир и термостат. Такое измерение проводят в основном в специально оснащенных лабораториях. Взвесьте прибор на аналитических весах, которые дают высокую точность (до 0,0002 г). Заполните его дистиллированной водой, чуть выше расположения метки, и закройте пробкой. Поместите пикнометр в термостат и выдержите 20 минут при температуре 20оС. Уменьшите количество воды до метки. Излишки уберите пипеткой и снова закройте пикнометр. Поместите его в термостат на 10 минут, проверьте, совпадает ли уровень жидкости с меткой. Протрите пикнометр снаружи мягкой салфеткой и оставьте на 10 минут за стеклом коробки аналитических весов, после чего снова взвесьте. Узнав таким образом точную массу прибора, вылейте из него воду, сполосните спиртом и эфиром, продуйте. Заполните пикнометр жидкостью, плотность которой нужно узнать, и действуйте точно так же, как и с дистиллированной водой.
Если нет специального прибора, можно измерить плотность с помощью весов и мерной мензурки. Поставьте на весы мензурку и уравновесьте чашечки. Запишите массу. Наполните мензурку исследуемой жидкостью на заданную единицу объема и снова взвесьте. Разница в массах является массой жидкости в заданном объеме. Поделив массу на объем, вы получите плотность.
Источник
Как узнать давление газа в сосуде
Отвечая на первый, из поставленных выше, вопрос, предположим, что давление газов на стенки сосуда объясняется ударами молекул .
Для того, чтобы в процессе поиска расчетной формулы этого давления ограничиться знаниями элементарной математики и физики, введем некоторые упрощения .
- Форма, строение молекул достаточно сложны. Но попробуем представить их в виде маленьких шариков. Это позволит нам применить к описанию процесса удара молекул о стенки сосуда законы механики, в частности, второй закон Ньютона .
- Будем считать, что молекулы газа находятся на достаточно большом расстоянии друг от друга, так, что силы взаимодействия между ними пренебрежимо малы. Если между частицами отсутствуют силы взаимодействия, соответственно, равна нулю и потенциальная энергия взаимодействия . Назовем газ, отвечающий этим свойствам, идеальным .
- Известно, что молекулы газа движутся с разными скоростями . Однако, усредним скорости движения молекул и будем считать их одинаковыми .
- Предположим, что удары молекул о стенки сосуда абсолютно упругие (молекулы ведут себя при ударе подобно резиновым мячикам, а не подобно куску пластилина). При этом скорости молекул изменяются лишь по направлению, а по величине остаются прежними. Тогда изменение скорости каждой молекулы при ударе равно –2υ.
Введя такие упрощения, рассчитаем давление газа на стенки сосуда.
Давление – это физическая величина, равная отношению перпендикулярной составляющей силы, действующей на поверхность, к площади этой поверхности.
Сила действует на стенку со стороны множества молекул. Она может быть рассчитана как произведение силы, действующей со стороны одной молекулы, на число молекул, движущихся в сосуде в направлении этой стенки. Так как пространство трехмерно и каждое измерение имеет два направления: положительное и отрицательное, можно считать, что в направлении одной стенки движется одна шестая часть всех молекул (при большом их числе): .
Сила, действующая на стенку со стороны одной молекулы, равна силе, действующей на молекулу со стороны стенки. Сила, действующая на молекулу со стороны стенки, равна произведению массы одной молекулы на ускорение, которое она получает при ударе о стенку:
Ускорение же – это физическая величина, определяемая отношением изменения скорости ко времени, в течение которого это изменение произошло: .
Изменение скорости равно удвоенному значению скорости молекулы до удара: .
Если молекула ведет себя подобно резиновому мячику, нетрудно представить процесс удара: молекула, ударяясь, деформируется. На процесс сжатия и разжатия затрачивается время. Пока молекула действует на стенку сосуда, о последнюю успевает удариться еще некоторое число молекул, находящихся от нее на расстояниях не дальше . (Например, условно говоря, пусть молекулы имеют скорость 100 м/с. Удар длится 0,01 с. Тогда за это время до стенки успеют долететь и внести свой вклад в давление молекулы, находящиеся от нее на расстояниях 10, 50, 70 см, но не далее 100 см).
Будем рассматривать объем сосуда .
Подставив все формулы в исходную, получаем уравнение:
где:
– масса одной молекулы, – среднее значение квадрата скорости молекул, – число молекул в объеме .
Сделаем некоторые пояснения по поводу одной из величин, входящих в полученное уравнение.
Так как движение молекул хаотично и преимущественного движения молекул в сосуде нет, их средняя скорость равна нулю. Но ясно, что это не относится к каждой отдельной молекуле.
Для вычисления давления идеального газа на стенку сосуда используется не среднее значение -компоненты скорости молекул
а среднее значение квадрата скорости
Чтобы введение этой величины было более понятным, рассмотрим численный пример.
Пусть четыре молекулы имеют скорости 1, 2, 3, 4 усл. ед.
Квадрат среднего значения скорости молекул равен:
Среднее значение квадрата скорости равно:
Если скорости молекул равны +1, –2 , –3 , +4 усл. ед., то квадрат среднего значения скорости равен:
Среднее значение квадрата скорости равно:
Средние значения проекций квадрата скорости на оси связаны со средним значением квадрата скорости соотношением:
Если извлечь квадратный корень из
то получим величину, которая называется средней квадратичной скоростью молекул.
Величина, определяемая отношением числа частиц к объему, в котором они находятся, называется концентрацией (обозначается буквой ).
Величина же
– это средняя кинетическая энергия каждой молекулы газа.
С учетом этого полученное уравнение можно переписать в виде:
Уравнения связывают макропараметры газа – его давление и объем () с микропараметрами – массой молекул и их скоростью (), или энергией
Последнее уравнение читается следующим образом: давление идеального газа на стенки сосуда прямо пропорционально концентрации молекул в сосуде и их средней кинетической энергии .
Источник
Источник
