Как вычислить диаметр сосуда

С помощью онлайн калькулятора вы сможете вычислить диаметр круга через формулы. Чтобы вычислить диаметр круга, просто введите ваши данные.
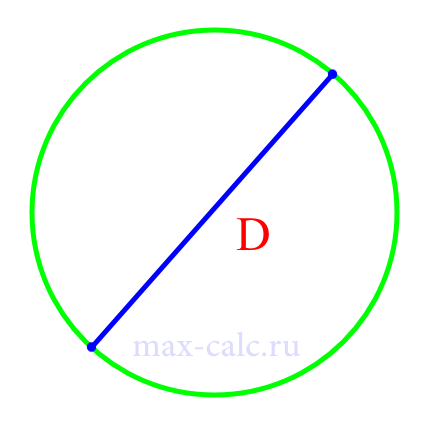
- Хорда, проходящая через центр окружности, называется диаметром.
- Центр окружности является серединой любого диаметра.
- Диаметр, делит круг на две равные части.
- Диаметр круга равен отношению периметра на π.
- Диаметр круга равен отношению периметра описанного квадрата на 4.
- Диаметр круга равен отношению двух сторон вписанного квадрата на корень из двух.
- Диаметр круга равен корню площади описанного квадрата.
- Диаметр круга равен корню двух площадей вписанного квадрата.
- Диаметр круга равен отношению двух сторон вписанного равностороннего треугольника на корень из трех.
- Диаметр круга равен отношению стороны описанного равностороннего треугольника на корень из трех.
- Диаметр круга равен высоте описанной трапеции.
- Диаметр круга равен стороне описанного квадрата.
Диаметр круга через длину окружности.
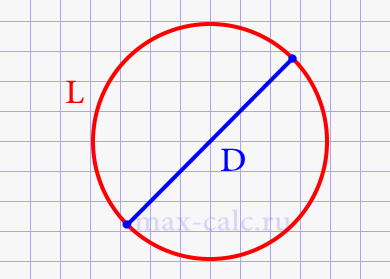
D = L π
Где: L – длина окружности, π – 3,14.
×
Длина окружности (L): мм
Диаметр (D) = мм
Диаметр круга через площадь круга.
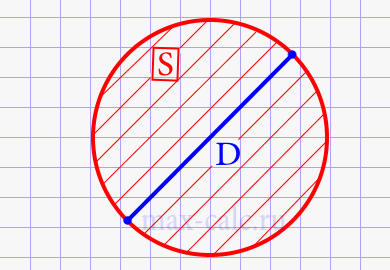
Где: S – площадь круга, π – 3,14.
×
Площадь (S): мм²
Диаметр (D) = мм
Диаметр круга через периметр описанного квадрата.
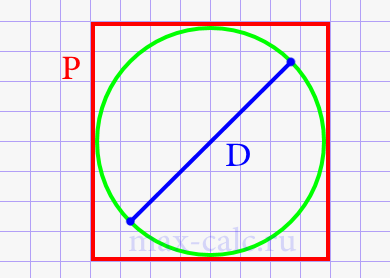
D = P 4
Где: P – периметр описанного квадрата.
×
Периметр (P): мм
Диаметр (D) = мм
Диаметр круга через площадь описанного квадрата.
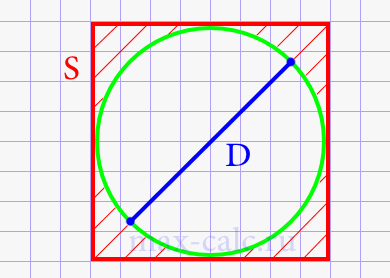
Где: S – площадь описанного квадрата.
×
Площадь (S): мм²
Диаметр (D) = мм
Диаметр круга через сторону описанного квадрата.
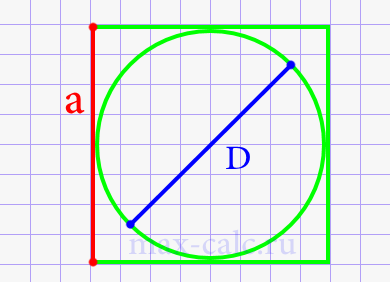
D = a
Где: a – сторона описанного квадрата.
×
Сторона (a): мм
Диаметр (D) = мм
Диаметр круга через сторону описанного равностороннего треугольника.
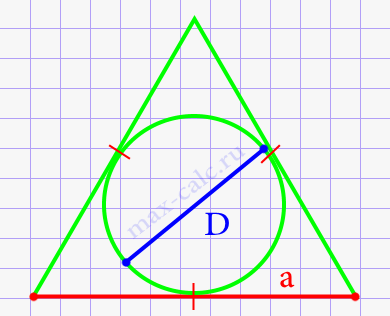
Где: a – сторона описанного равностороннего треугольника.
×
Сторона (a): мм
Диаметр (D) = мм
Диаметр круга через периметр вписанного квадрата.
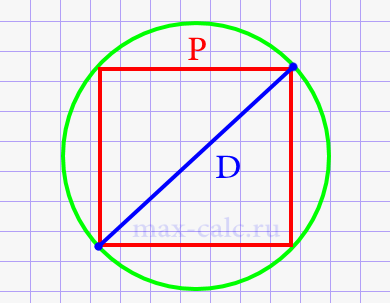
Где: P – периметр вписанного квадрата.
×
Периметр (P): мм
Диаметр (D) = мм
Диаметр круга через площадь вписанного квадрата.
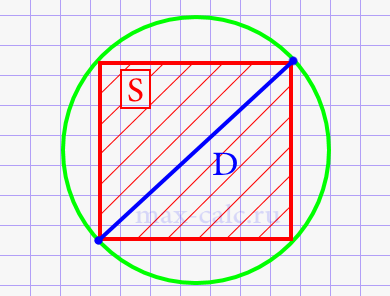
Где: S – площадь вписанного квадрата.
×
Площадь (S): мм²
Диаметр (D) = мм
Диаметр круга через сторону вписанного квадрата.
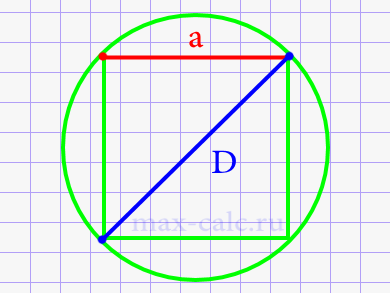
Где: a – сторона вписанного квадрата.
×
Сторона (a): мм
Диаметр (D) = мм
Диаметр круга через сторону вписанного равностороннего треугольника.
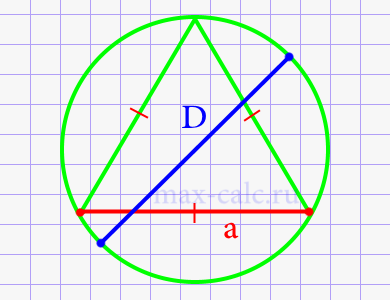
Где: a – сторона вписанного равностороннего треугольника.
×
Сторона (a): мм
Диаметр (D) = мм
Диаметр круга через стороны и диагональ вписанной равнобедренной трапеции.
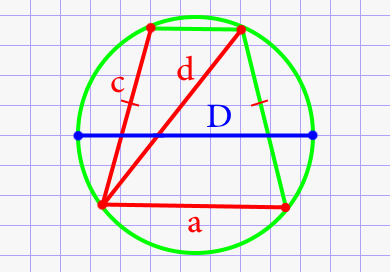
p = a + c + d 2
Где: a – большее основание, c – боковая сторона, d – диагональ трапеции.
×
Основание (a): мм
Сторона (c): мм
Диагональ (d): мм
Диаметр (D) = мм
Диаметр круга через высоту описанной трапеции.
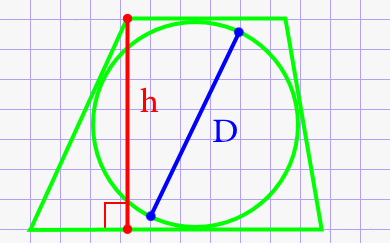
D = h
Где: h – высота трапеции.
×
Высота (h): мм
Диаметр (D) = мм
Источник
Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?
Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.
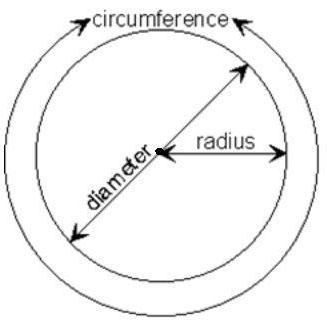
Круг и окружность
Окружностью является множество точек, которые размещены на равном расстоянии от основной точки – центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.
А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.
Формула окружности через диаметр
Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр – d. Поскольку соотношение длины очертания и диаметра – постоянное число, то его можно определить.
Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.
Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.
Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π – это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).
Как вычислить диаметр: формула
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.

Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас – изготовить крышку. Что будем делать в таком случае?
Нужно воспользоваться формулой. Возьмем длину очертания колодца – к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Источник
Калькулятор круга
Удобный онлайн сервис для расчета радиуса, диаметра, длинны окружности, площади круга и шара, объема шара. Просто введите значение известного Вам параметра в поле “значение” выберите известный параметр и нажмите кнопку рассчитать.
Для увеличения точности и качества вычисления калькулятор круга использует число Пи с точностью до десятого знака после запятой.
Общий механизм вычисления всех представленных параметров сходен. В независимости от того, какой параметр вы вводите, в первую очередь вычисляется радиус. На основе радиус строятся все последующие вычисления.
Калькулятор шара
Калькулятор шара – это одна из функций нашего калькулятора круга. Благодаря ему вы с легкостью можете рассчитать такие сложные параметры, как объем шара или его площадь. Основное удобство заключается в том, что можно легко перейти от площади шара к его объему.
Калькулятор круга – это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR2. Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr3). Она была использована при создании нашего онлайн сервиса. Сайт tellall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Свежие статьи
Источник
