Как вычислить обьем сосуда
2 октября 2011
Автор КакПросто!
Объем определяет величину пространства, которую занимает какое-либо тело. Эта величина связана постоянными соотношениями с другими характеристиками физических тел – их геометрическими размерами, весом и плотностью. Поэтому измерение этих дополнительных параметров может стать базой для вычисления объема, например, сосуда.
Инструкция
Если есть возможность наполнить сосуд водой, то для определения его объема достаточно иметь какую-либо мерную форму. В зависимости от размеров сосуда мерной посудой может стать шприц, мензурка, стакан, банка, ведро или любая другая посуда, вместимость которой вам известна. Подобрав подходящий измерительный сосуд, заполните водой до краев сосуд исследуемый, а затем переливайте воду в измерительный сосуд, отсчитывая таким образом объем.
Если заполнить исследуемый сосуд жидкостью нет возможности, но можно поместить его в жидкость, то определите объем по количеству вытесненной им воды. Для этого тоже потребуется какая-либо мерная посуда. Заполнив ее частично водой, отметьте уровень, затем поместите в мерную посуду исследуемый сосуд таким образом, чтобы он полностью оказался под водой, и сделайте вторую отметку. Затем определите разницу объемов мерной посуды по разнице двух сделанных отметок.
Если мерной посуды нет, но есть возможность взвешивать сосуд, то определите разницу между сосудом пустым и заполненным водой. Исходя из того, что один кубический метр объема должен вмещать воду, весом в одну тонну, рассчитайте объем сосуда.
Если сосуд имеет геометрически правильную форму, то его объем можно рассчитать, измерив размеры. Для нахождения объема сосуда цилиндрической формы (например, кастрюли) надо измерить диаметр (d) его основания (дна кастрюли) и ее высоту (h). Объем (V) будет равен одной четверти от произведения возведенного в квадрат диаметра на высоту и число Пи: V=d²∗h∗π/4.
Для нахождения объема сосуда, имеющего форму шара, достаточно определить его диаметр (d). Объем (V) будет равен одной шестой части от произведения возведенного в куб диаметра на число Пи: V=d³∗π/6. Если измерить длину окружности (L) шарообразного сосуда в самой широкой его части проще (например, с помощью сантиметра), чем измерить диаметр, то объем можно рассчитать и через эту величину. Возведенную в куб длину окружности надо разделить на увеличенное в шесть раз число Пи, возведенное в квадрат: V=L³/(π²∗6).
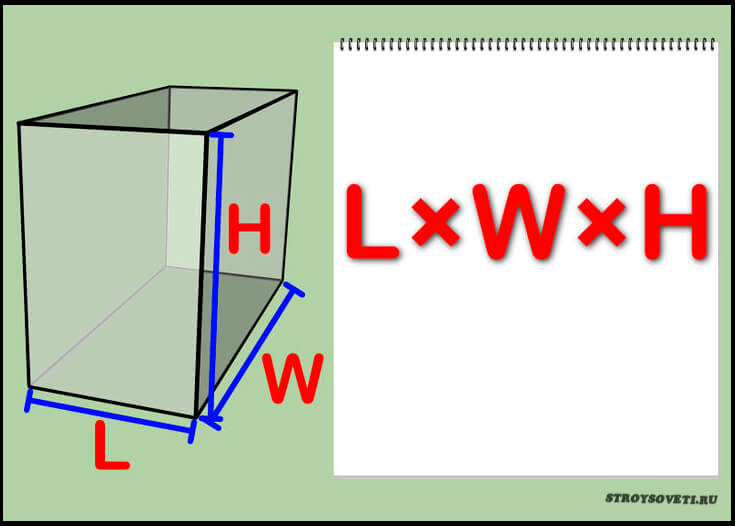
Для нахождения объема (V) сосуда прямоугольной формы, надо измерить его длину, ширину и высоту (a, b и h) и перемножить полученные значения: V=a∗b∗h. Если этот сосуд имеет кубическую форму, то достаточно возвести длину одного его ребра в третью степень: V=a³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Источник
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 – интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 – интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 – интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 – интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 – интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
Что такое вместимость сосуда
Вместимость сосуда – это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ – кубический метр, но в случае жидкости чаще используют литр.
Особенности расчета объема жидкости в сосуде
Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества – твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.
В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.
За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:
(h = frac{p}{rho s g}.)
(p) здесь – давление в паскалях, (rho) – плотность, (g) – ускорение свободного падения, константа.
Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.
При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов.
Задача
Найти объем керосина, зная массу одного и того же сосуда с ним, и без него. Масса пустого сосуда 440 грамм, полного – 600 грамм.
Решение:
Плотность керосина можно узнать из справочной таблицы – 800 (frac{кг}{м^{3}}.)
Вычислим массу керосина в сосуде: 600 – 440 = 160.
Подставим известные данные в формулу:
(V = frac{m}{rho} = frac{0,16}{800} = 0,0002 м^{3} = 200 см^{3}.)
Ответ: 200 (см^{3}.)
Как определить вместимость сосудов разных форм
Вычисление объема параллелепипеда
Параллелепипед – это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.
(V = S_{осн} s H. )
Прямоугольный параллелепипед – это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, – это куб.
Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
(V = AB s AD s AA_{1} = abc.)
Объем куба равен кубу его стороны:
(V = a^{3}.)
Нахождение объема пирамиды
Пирамида – это многогранник, состоящий из основания – плоского многоугольника, вершины – точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды – это перпендикуляр, опущенный из вершины на плоскость основания.
(V = frac{1}{3} s S_{осн} s h.)
Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований – (S_{1}) и (S_{2}).
(V = frac{1}{3} s h s (S_{1} + S_{2} + sqrt{S_{1} s S_{2}}). )
Как найти объем цилиндра
Цилиндр – это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
(R) – радиус основания цилиндра, (h) – его высота, равная образующей оси.
(V = S_{осн} s h = pi s R^{2} s h.)
Если нужно найти объем усеченного цилиндра, то понадобится не только R – радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l – (l_{1}) и (l_{2}).
(V = pi s R^{2} s frac{l_{1} + l_{2}}{2}.)
Как высчитать объем конуса
Конус – это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.
(V = frac{1}{3} s S_{осн} s h = frac{1}{3} s pi s R^{2} s h.)
Чтобы найти объем усеченного конуса, понадобятся (R_{1}) и (R_{2}) – радиусы оснований, а также высота (h).
(V = frac{pi s h}{3} s (R_1^2 + R_2^2 + R_1 s R_2).)
Нахождение объема шара
Шар – это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.
(R) – радиус полукруга, равный радиусу шара.
(V = frac{4pi s R^{3}}{3}.)
Источник
Резервуары и цистерны используются для перевозки и хранения различных видов топлива, нефти, воды и газа, некоторых строительных материалов, химических веществ, а также пищевых продуктов. Многие не знают, как рассчитать объем емкости, ведь они могут иметь различную геометрическую форму:
- Конуса;
- Цилиндра;
- Сферы;
- Прямоугольного параллелепипеда.
В нашей статье ознакомимся с нюансами расчёта для конкретных геометрических тел.
Как узнать объём прямоугольной тары
В сфере строительства все показатели объёма приведены к конкретным величинам. Расчёты могут проводиться в литрах или дм3, но чаще всего для определения количества того или иного материала используются кубические метры. Как рассчитать кубатуру самых простых прямоугольных ёмкостей опишем дальше на конкретном примере.

Для работы нам понадобится тара, строительная рулетка и блокнот с ручкой или карандашом для проведения вычислений. Из курса геометрии известно, что объём подобных тел вычисляется умножением длины, ширины и высоты изделия. Формула расчётов сводится к следующему
V=a*b*c, где a, b и с – стороны тары.
Например, длина нашего изделия равняется 150 сантиметрам, ширина 80 сантиметрам, высота 50 сантиметров. Для правильного подсчёта кубатуры указанные величины переводим в метры и проводим необходимые расчёты V=1,5*0,8*0,5=0,6м3.
Как определить объём сферического изделия
Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.
Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:
- V – подсчитываемый объём детали;
- R- радиус сферы;
- ԉ – постоянная величина, которая равняется 3,14.
Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.
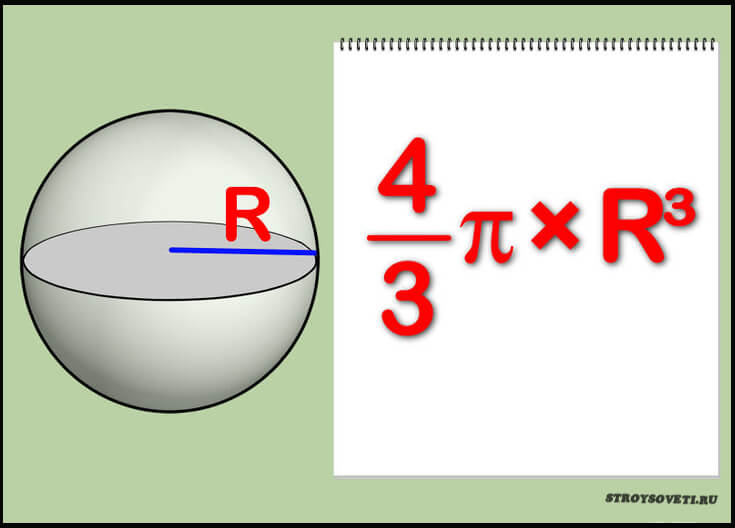
А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу:
V= (4*3,14*0,8³)/3=2,14м³
Как вычислить объём цистерны выполненной в виде цилиндра
Подобные геометрические фигуры используются для хранения пищевых продуктов, транспортирования топлива и других целей. Многие не знают, как рассчитать объем воды, но основные нюансы такого процесса опишем дальше в нашей статье.
Высоту жидкости в цилиндрической ёмкости определяют по специальному устройству метрштоку. В данном случае емкость цистерны вычисляется по специальным таблицам. Изделия со специальными таблицами измерения объёма в жизни встречаются редко, поэтому подойдём к решению проблемы другим путём и опишем, как рассчитать объём цилиндра по специальной формуле – V=S*L, где
- V- объём геометрического тела;
- S – площадь сечения изделия в конкретных единицах измерения (м³);
- L – длина цистерны.
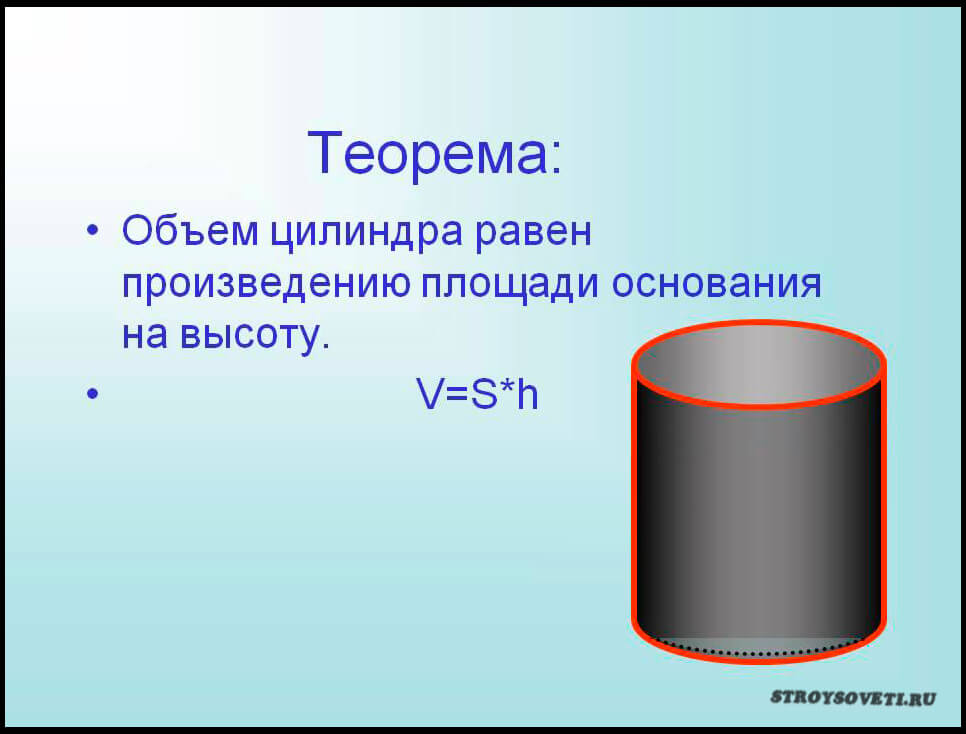
Показатель L можно измерить при помощи всё той же рулетки, но площадь сечения цилиндра придётся считать. Показатель S вычисляют по формуле S=3,14*d*d/4, где d – диаметр окружности цилиндра.
А теперь ознакомимся с конкретным примером. Допустим, длина нашей цистерны имеет значение 5 метров, её диаметр 2,8 метра. Сначала вычислим площадь сечения геометрической фигуры S= 3,14*2,8*2,8/4=6,15м. А теперь можно приступать к вычислению объёма цистерны 6,15*5= 30,75 м³.
Источник
Резервуары и цистерны используются для перевозки и хранения различных видов топлива, нефти, воды и газа, некоторых строительных материалов, химических веществ, а также пищевых продуктов. Многие не знают, как рассчитать объем емкости, ведь они могут иметь различную геометрическую форму:
- Конуса;
- Цилиндра;
- Сферы;
- Прямоугольного параллелепипеда.
В нашей статье ознакомимся с нюансами расчёта для конкретных геометрических тел.
Как узнать объём прямоугольной тары
В сфере строительства все показатели объёма приведены к конкретным величинам. Расчёты могут проводиться в литрах или дм3, но чаще всего для определения количества того или иного материала используются кубические метры. Как рассчитать кубатуру самых простых прямоугольных ёмкостей опишем дальше на конкретном примере.
Для работы нам понадобится тара, строительная рулетка и блокнот с ручкой или карандашом для проведения вычислений. Из курса геометрии известно, что объём подобных тел вычисляется умножением длины, ширины и высоты изделия. Формула расчётов сводится к следующему
V=a*b*c, где a, b и с – стороны тары.
Например, длина нашего изделия равняется 150 сантиметрам, ширина 80 сантиметрам, высота 50 сантиметров. Для правильного подсчёта кубатуры указанные величины переводим в метры и проводим необходимые расчёты V=1,5*0,8*0,5=0,6м3.
В чем сложность расчет объема емкости?
Для хранения или транспортировки таких веществ как метан, нефть, бензин, молоко, вода требуется емкость с определенным литражом, который на практике требуется знать в кубах, а иногда и в килограммах. Порой возникает необходимость перевода литров в тонны.
Формула расчета объема для различных веществ проста, но на практике часто встречаются ошибки. Поэтому не будет лишним уделить несколько минут и проверить себя, воспользовавшись нашим калькулятором. Ведь ошибка при решении задачи может быть чревата, только плохой оценкой, а на практике неверные расчеты могут привести к приобретению емкости с недостаточным объемом, а ведь это лишние траты.
Как определить объём сферического изделия
Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.
Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:
- V – подсчитываемый объём детали;
- R- радиус сферы;
- ԉ – постоянная величина, которая равняется 3,14.
Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.
А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу:
V= (4*3,14*0,8³)/3=2,14м³
Инструктивные указания по определению веса наливных грузов в цистернах
Поэтапный расчет
Чтобы вычислить объем бочки, формула должна быть такого вида:
(πh / 12) x (2D2 + d2)
Замените значения в приведенной выше формуле = [(π x 10) / 12] = 2,61 х 873 = 2285,50 кубических дюйма.
1 кубический дюйм содержит 0,016387 литров. Чтобы найти объем цилиндра в литрах, умножьте 2285,50 дюйма на 0,016387 л = 2285,50 х 0,016387 = 37,45 литра.
1 кубический дюйм содержит 0.00432899 US жидкого галлона. Чтобы найти объем цилиндра в жидких галлонах США, умножьте 2285,50 с 0,00432899 галлонов = 2285,50 х 0,00432899 = 9,89 жидких галлонов США.
Если входные значения указываются в футах, целесообразно будет обратиться к таблице ниже для вычисления коэффициента преобразования. Соответствующий коэффициент пересчета следует умножить на результат, рассчитанный по приведенной выше математической формуле, чтобы найти объем.
Объем цилиндра может потребоваться для расчета в SI, метрических или обычных системах, поэтому калькулятор объема наделен функцией преобразования основных единиц измерения, чтобы находить выходные значения в разных единицах, таких как:
- литры (L);
- галлоны (галлон);
- кубические дюймы (дюймы);
- кубические футы (футы);
- кубические метры (м);
- кубические сантиметры (см);
- кубические миллиметры (мм).
Используя таблицу преобразования, можно определить такие показатели:
- 1 кубический дюйм = 0,016387 литра;
- 1 кубический дюйм = 0,00360464 галлон;
- 1 кубический дюйм = 0,00432899 US жидкий галлон;
- 1 кубический фут = 28,3168 литров;
- 1 кубический фут = 6,22884 галлон;
- 1 кубический фут = 7,48052 US жидкий галлон.
Будь то резервуар для воды, банка краски или пробирка, каждый цилиндрический контейнер имеет две общие характеристики:
- круглое поперечное сечение;
- конкретное расширение в пространстве, называемое его длиной или высотой.
Если необходимо узнать емкость цилиндра, сколько он способен вместить, рассчитывают его объем. Для этого имеется простая формула, но есть один нюанс
Важно учитывать толщину стен контейнера. В большинстве случаев это количество незначительно, но не всегда
Еще одна вещь: емкость обычно измеряется в галлонах или литрах, поэтому, если нужны эти единицы, придется конвертировать из кубических футов, дюймов или других метрических единиц.
Вычислить объем поможет формула V = πr2h или V = (πd2h) / 4. Поскольку толщина влияет на показатели внешнего объема, необходимо измерить внутренние размеры, если цилиндр имеет толстые стенки.
Определяем объём бочки: лёгкие формулы, практические советы
В последнее время все чаще в хозяйстве используется бондарная продукция. Это объясняется не только её красивым внешним видом, но и экологичностью. Засоленные в кадке огурцы или капуста, залитый выдавленный из винограда сок, который в последующем превратится в ароматный алкогольный напиток – лучшего места для хранения разной жидкости и заготовок не найти. Сейчас большие двухсотлитровые кадки используются даже для сооружения современных вертикальных грядок, на которых выращивают овощи и ягоды. Учитывая широкую область применения ёмкостей, хозяйкам надо понимать, как вычислить объем бочки. Многие сосуды имеют цилиндрическую форму, поэтому получить необходимые параметры не так уж и сложно. Вычислить объём выпуклой бочки (её ещё называют «пузатая») сможет не каждая хозяйка. В данном случае нужно не просто измерить внутренний диаметр сосуда и его высоту. Всё гораздо сложнее.
Поэтапный расчет
Чтобы вычислить объем бочки, формула должна быть такого вида:
(πh / 12) x (2D2 + d2)
Замените значения в приведенной выше формуле = [(π x 10) / 12] = 2,61 х 873 = 2285,50 кубических дюйма.
1 кубический дюйм содержит 0,016387 литров. Чтобы найти объем цилиндра в литрах, умножьте 2285,50 дюйма на 0,016387 л = 2285,50 х 0,016387 = 37,45 литра.
1 кубический дюйм содержит 0.00432899 US жидкого галлона. Чтобы найти объем цилиндра в жидких галлонах США, умножьте 2285,50 с 0,00432899 галлонов = 2285,50 х 0,00432899 = 9,89 жидких галлонов США.
Если входные значения указываются в футах, целесообразно будет обратиться к таблице ниже для вычисления коэффициента преобразования. Соответствующий коэффициент пересчета следует умножить на результат, рассчитанный по приведенной выше математической формуле, чтобы найти объем.
Объем цилиндра может потребоваться для расчета в SI, метрических или обычных системах, поэтому калькулятор объема наделен функцией преобразования основных единиц измерения, чтобы находить выходные значения в разных единицах, таких как:
- литры (L);
- галлоны (галлон);
- кубические дюймы (дюймы);
- кубические футы (футы);
- кубические метры (м);
- кубические сантиметры (см);
- кубические миллиметры (мм).
Используя таблицу преобразования, можно определить такие показатели:
- 1 кубический дюйм = 0,016387 литра;
- 1 кубический дюйм = 0,00360464 галлон;
- 1 кубический дюйм = 0,00432899 US жидкий галлон;
- 1 кубический фут = 28,3168 литров;
- 1 кубический фут = 6,22884 галлон;
- 1 кубический фут = 7,48052 US жидкий галлон.
Будь то резервуар для воды, банка краски или пробирка, каждый цилиндрический контейнер имеет две общие характеристики:
- круглое поперечное сечение;
- конкретное расширение в пространстве, называемое его длиной или высотой.
Если необходимо узнать емкость цилиндра, сколько он способен вместить, рассчитывают его объем. Для этого имеется простая формула, но есть один нюанс
Важно учитывать толщину стен контейнера. В большинстве случаев это количество незначительно, но не всегда
Еще одна вещь: емкость обычно измеряется в галлонах или литрах, поэтому, если нужны эти единицы, придется конвертировать из кубических футов, дюймов или других метрических единиц.
Вычислить объем поможет формула V = πr2h или V = (πd2h) / 4. Поскольку толщина влияет на показатели внешнего объема, необходимо измерить внутренние размеры, если цилиндр имеет толстые стенки.
| 1. Общие положения 2. Определение объема жидкости в цистернах 3. Определение плотности жидкости 4. Способ определения веса жидкости в цистернах по замеру 5. Постановка калибровочных знаков и клейм на цистернах 1. Общие положения В соответствии с правилами перевозки грузов наливом в цистернах вес этих грузов определяется в результате установления путем замера объема налитого груза . Для того чтобы иметь возможность определить объем груза, все цистерны в зависимости от конструкции котлов и размеров их элементов (барабанов, днищ и колпаков) подразделяются на ряд калибровочных типов. Чтобы облегчить процесс определения количества груза, который может быть расположен на любом уровне котла цистерны или надкотловой части (колпака, люка), для каждого типа цистерн составлена отдельная таблица поинтервальной калибровки. В таблице объем цистерны разбит с сантиметровыми интервалами, начиная от основания (нижней образующей) котла, и указаны объемы, соответствующие каждому из этих уровней, в кубических дециметрах (литрах). Калибровочные данные, расположенные выше выделенных жирным шрифтом, представляют собой сумму полной вместимости котла и заполненной части колпака. Значения вместимости в таблицах округлены до значения, кратного 5. 2. Определение объема жидкости в цистернах Объем жидкости в цистернах определяется по таблицам калибровки железнодорожных цистерн исходя из типа цистерны и высоты налива. Калибровочный тип цистерны обозначается металлическими цифрами, приваренными к боковой поверхности котла под номером цистерны. Для ясной видимости цифры окрашиваются в белый или черный цвет в зависимости от цвета окраски котла. Высота налива определяется специальным измерительным прибором – метрштоком. Метршток представляет собой металлическую трубу 2 (рис. 1,а) диаметром 20-25 мм с длиной шкалы до 3500 мм. Цена наименьшего деления шкалы 1 мм. Пятисантиметровые и дециметровые штрихи имеют числовое обозначение количества сантиметров, начиная от . Штрихи, отмечающие целые метры, обозначены цифрами с буквой , например . Нижний конец прибора имеет медный наконечник 1, а верхний- металлическое кольцо 3 или серьгу. Для замеров разрешается пользоваться и деревянными брусковыми метрштоками (рис. 1, б), изготовляемыми из дерева твердых пород. Размеры сечения бруса 4 должны быть: при квадратном сечении – сторона квадрата 40-50 мм; при прямоугольном – (3040) х (5060) мм. К деревянному брусу прикрепляется металлическая пластина 5 (толщиной не менее 1,5 мм, шириной 20-25 мм) со шкалой. Нижний конец деревянного метрштока армируется медным наконечником 6. Метрштоки должны представляться в установленные сроки для проверки в областные, краевые или республиканские государственные контрольные лаборатории по измерительной технике. Метршток должен тщательно предохраняться от искривления. Хранить его рекомендуется только вертикально в подвешенном положении. Во время замера метршток плавно и строго вертикально опускается через люк колпака до самой нижней точки котла. При этом необходимо избегать резких ударов о дно цистерны и следить за тем, чтобы нижний конец метрштока не упирался в какую-либо выступающую деталь цистерны или в посторонний предмет и не попадал в углубление сливного прибора или поддона. Опущенный до нормального положения метршток быстро, но плавно извлекается и по линии смачивания на нем определяется высота слива в сантиметрах. Отсчет должен производиться так чтобы линия смачивания была на уровне глаз производящего отсчет. Высота налива замеряется метрштоком в двух противоположных точках люка (колпака) по продольной осевой линии цистерны не менее двух раз в каждой точке. Расхождение между двумя отсчетами замера не должно превышать 0,5 см. В случае расхождения, превышающего 0,5 см, измерение повторяется. За действительную высоту налива принимается среднее арифметическое результатов замеров, произведенных в двух противоположных точках. Полученный результат округляется до целого сантиметра, т.е. величина менее 0,5 см отбрасывается, а 0,5 см и более считается за целый сантиметр. При измерении высоты налива светлых нефтепродуктов (бензина, лигроина, керосина) металлическим метрштоком рекомендуется шкалу прибора в границах предполагаемого отсчета натереть мелом и слегка протереть для лучшего определения линии смачивания. По высоте налива в сантиметрах для каждого калибровочного типа по соответствующей таблице калибровки определяется объем налитой жидкости в кубических дециметрах (дм.куб). Пример . Тип цистерны 72. Высота налива, определенная метрштоком, 274,6 см (2746 мм). Установить объем жидкости в цистерне. Округляя до целого сантиметра, получим высоту налива 275 см. По таблице калибровки для цистерн типа 72 этой высоте налива соответствует объем, равный 69191 дм.куб. От правильности замера высоты налива зависит точность определения объема, а значит, и веса груза в цистерне, поэтому на тщательность замера высоты налива должно быть обращено самое серьезное внимание. Операции с метрштоком (погружение в жидкость, извлечение из цистерны и отсчет по линии смачивания) во избежание ошибок должны производиться тщательно. При извлечении метрштока из цистерн, особенно после замера темных и тем более вязких нефтепродуктов, необходимо следить, чтобы продукт не разбрызгивался и не загрязнял цистерну снаружи. Извлеченный из цистерны метршток должен быть насухо протерт. Большое влияние на точность определения высоты налива оказывает состояние замеряемой жидкости и ее поверхности. При наливе цистерн жидкость часто насыщается воздухом, а также на ее поверхности образуется слой пены. Из-за этого искажаются в сторону завышения результаты замеров. Поэтому замер высоты налива должен производиться после некоторого отстоя продукта при спокойной поверхности жидкости и отсутствии на ней пены. Влияние слоя пены на определение уровня налива может быть исключено путем замера высоты налива при помощи очень простого приспособления, называемого пеноизолятором. |
Источник
